H-Net - Engineering (1gpu)

To obtain scaling laws for any architecture, we must implement hardware-efficient training.

Desiderata

#

For small scale research runs, the following minimal criteria are ideal:

1. Compute blocks are torch.compile’able, with fullgraph=True.
2. Minimal CPU overhead / CUDA syncronization each train step.

Naturally, it is possible to optimize small scale runs much further than this. For example, you could compile an entire model’s train step, and capture it as a CUDAGraph.

However, as a sole individual, working on an architecture with inherent shape dynamism, I refrain from going all in, and limit myself to simple optimizations.

Block Compilation

#

In my original code from July, I described my code as “block-compilable”.

While technically true (it did not produce errors), it did not produce anything close to optimal performance, as it involved many graph breaks. The published MFU graphs were also simply wrong due to drastic overestimation of the inner hierarchy’s sequence lengths.

In reality, it takes significant effort to make an individual H-Net block compilable, especially for arbitrary hierarchies && sequence lengths.

Mamba2

#

The first major roadblock against efficient H-Net training is the Mamba2 layer, and specifically its gigantic mamba_split_conv1d_scan_combined method.

Many past users of Mamba2 have complained about the impossibility of compiling && the extreme slowness of it at small scale, to which the official reply is to “use a large model”.

This seemed unreasonable to me, so I attempted to compile the model anyway. As it turns out, that is quite hard.

causal-conv1d

#

The first issue that presents itself is the incompatibility of torch.compile with custom_ops that have non-contiguous inputs.

I patch this by subsuming the expected transpose into the custom_op wrapper.

Autotuning dependency

#

The next issue is a recurring problem throughout mamba’s triton kernels.

In many case, mamba’s kernels have the following programming pattern:

1. create output tensor y of size cdiv(seqlen,min(BLOCK_SIZES))
2. run kernel[...](y), with autotuning across BLOCK_SIZES
3. extract bs = kernel.best_config.kwargs[BLOCK_SIZE] from the best autotuned kernel, and use it to minimize future work on output y, e.g. y[:cdiv(seqlen,bs)].sum()

This is a disaster for torch.compile, as initial dynamo tracing does not execute any kernels, which means kernel.best_config no longer exists at compile time, causing code execution to error and explode…

Quick solution: bite the slight compute overhead, and sum over all blocks regardless of block size.

Also, many kernels use pre_hook to zero inputs during auto-tuning, but pre_hook is not supported by torch.compile. Luckily, reset_to_zero is, so switching to it is sufficient to permit compilation for all mamba kernels.

Additional misc problems

#

This commit addresses even more problems:

• Somehow, inductor inlines user-defined kernels in a way that forgets to import math if it is used. Manual substitutes for math methods resolves this.
• Inductor is unhappy if reset_to_zero tensors are only sometimes None. Use redundant tensors to avoid this.
• There is some internal torch confusion about the ordering of named & parametric arguments to triton kernels, which sorting solves.

Redundant clones

#

After all of that bullshit, mamba_split_conv1d_scan_combined is fullgraph compilable.

However, the naive compiled result is quite inefficient from a memory bandwidth perspective:

For example, the highlighted triton_poi_fused_2 above implemented a redundant copy of one empty tensor to another (i.e. copying uninitialized data):

The origins of this stem from another programming pattern in mamba’s source code, where

1. a large fused output tensor (e.g. dzxbcdt) is created
2. that tensor is .split(...,dim=-1) into subtensors, which is “free” in eager as it merely creates views with different strides
3. those split tensors are modified in-place, under the assumption that modifying them will also propagate writes to the root fused tensor dzxbcdt.

Unfortunately, real world kernels do not perform well if you have gaping holes between every row. Therefore, inductor tries to manually copy memory between fused<->chunk tensors.

Ultimately, this is highly redundant, and can be solved with some reasonable redefinition. This improves the execution time of small-scale mamba layers by roughly 20%, as they are primarily memory bandwidth bound.

Transformer

#

Since the rest of the isotropic block is defined the same way as a standard llama2 transformer, there are zero issues in fullgraphing each block.

One minor nit is that I patch/reimplement certain tridao kernels (rope, rmsnorm) to be more torch-compile friendly, as the existing public approach to supporting compile is “not wrapping it right”.

Block generalization

#

If you thought fixing all of that was sufficient to make block compilation work correctly, think again.

$S=0$ nets work correctly. And – in the pure “mamba $s=0$, transformer $s=1$” case – $S=1$ nets as well, by the undefined behavior of pytorch 2.7.

$S=2$ nets are broken. I don’t have a saved image, but it will produce some gobbledygook about hitting recompile limits on dynamic shapes.

The underlying issue is the original code’s treatment of all Isotropic layers as implementations of the same Block. Because,

• torch.compile treats all functions with the same code object (hash) as identical
• All Block.forward methods are the same object, and hence the same “function”

Dynamo’s interpretation of compiled H-Net blocks is thus equivalent to a ridiculously dynamic function which:

• has varying sequence length (ok)
• can either implement a mamba2 or transformer forward (ok…?)
• has parameters with dynamically varying hidden dim (very bad)

But I only need the first item on that list to be true. So, to sidestep this behavior, I transform the Block into a metaclass:

That ensures dynamo correctly specializes the compiled code, depending on the behavior of each block, and helps to fix $S>1$ nets by proxy.

Block overhead

#

In torchtitan, block compilation works quite well, as a motivated strategy to:

• obtain reasonable performance
• reduce compile time
• keep compilation composable with parallelism APIs

All those points are still true for H-Nets of sufficient size.

When you have insufficient size, this occurs:

Of course, those barriers are important, as they are responsible for triggering recompilation in the event of varied sequence lengths, and/or accidental external modifications to the global torch environment. So it would be bad to remove them completely.

On the other hand, executing them every block (which torch must do for generalized correctness) is a waste, if we know with certainty that a block is repeated. Therefore, I use the 2.8 nested_compile_region feature manually implement a bespoke strategy to evade guards in the event of a repeated layer variant:

After doing so, the compile guards only exist for the first layer an Isotropic:

Obviously, this is highly unsafe, and should only be done with the confident backing of someone who has worked on the torch.compile ecosystem extensively.

So, after we deal with all of those horrors, the performance of Isotropics are reasonably well-optimized.

Yet, if we look at the graph on a reasonably small $S=1$ model:

CPU Overhead

#

I do a few things to reduce CPU overhead at small scale:

1. train with 1gpu (FSDP2 ~doubles CPU overhead)
2. remove NJT (only used externally for debugging)
3. overlap d2h transfers with compute
4. implement $\mu$P-compatible foreach optimizers
5. pin socket affinity to reduce context-switching hangs

Most of these are well-known things, and don’t require much elaboration for the experienced.

But I’ll elaborate a bit on the parts that are pertinent/unique to H-Net.

Fused q/k/r vs D2H overlap

#

In a H-Net, the output of the encoder, $y_\texttt{enc}$, is used as immediate input to 3 linear layers:

• q_proj (1-padded routing)
• k_proj (routing)
• res_proj (post-main residual)

In aggregate, the full compute chain of routing + residual is like this:

def routing_and_residual(y_enc, cu_outer, w_q, w_k, w_res):
  r = y_enc @ w_res.mT
  k = y_enc @ w_k.mT
  q = QPaddedProj.apply(y_enc, w_q, k, cu_outer) # matmul + minor extra copies/padding

  p = (.5 - F.cosine_similarity(q,k,dim=-1)/2).clamp(.0,1.)
  b = p >= .5 
  cu_inner = F.pad(b.cumsum(0), (1,0))[cu_outer]

  # required immediately for main network input shape
  inner_seqlen = cu_inner[-1].item()
  inner_maxlen = cu_inner.diff().max().item()

  return p, b, cu_inner, inner_seqlen, inner_maxlen

One basic optimization you could commit, is to fuse all 3 of these linears into a single matmul (albeit a custom one, due to the need for padding on the BOS)

def routing_and_residual(y_enc, cu_outer, w_qkr):
  r,k,q = FusedQKR.apply(y_enc, w_qkr, cu_outer)

  p = (.5 - F.cosine_similarity(q,k,dim=-1)/2).clamp(.0,1.)
  b = p >= .5 
  cu_inner = F.pad(b.cumsum(0), (1,0))[cu_outer]

  # !!! Blocking D2H !!!
  inner_seqlen = cu_inner[-1].item()
  inner_maxlen = cu_inner.diff().max().item()

  return p, b, cu_inner, inner_seqlen, inner_maxlen

But, another competing optimization target is the compute bubble implied by that D2H, which could instead be overlapped with the computation of r:

def routing_and_residual(y_enc, cu_outer, w_q, w_k, w_res):
  k = y_enc @ w_k.mT
  q = QPaddedProj.apply(y_enc, w_q, k, cu_outer)

  p = (.5 - F.cosine_similarity(q,k,dim=-1)/2).clamp(.0,1.)
  b = p >= .5 
  cu_inner = F.pad(b.cumsum(0), (1,0))[cu_outer]

  # typical d2h compute overlap pattern
  stats_gpu = torch.stack([cu_inner[-1], cu_inner.diff().max()])
  stats_cpu = torch.empty_like(stats_gpu, device='cpu', pin_memory=True)
  stats_cpu.copy_(stats_gpu, non_blocking=True)
  e = torch.cuda.Event(); e.record()
  # do compute in here
  r = y_enc @ w_res.mT
  # pause until event, GPU not fully starved of work
  e.synchronize()

  return p, b, cu_inner, *stats_cpu.tolist()

If you fused all q/k/res into a single kernel, it would no longer be possible (at torch level) to signal the arrival of stats_cpu prior to all matmul compute finishing.

So, in practice, I op for the latter approach, rather than the former.

NJT overhead

#

Ignoring performance, the most natural way to express the H-Net architecture is via NJT:

The computational flow of the above code is natural & obvious.

But, in terms of the CPU bottleneck – it’s quite the disaster, no way around it.

Pure eager mode execution of NJTs will easily double CPU overhead.

NJTs are supposed to shine when used in conjunction with torch.compile to obtain fused varlen ops. But,

• that won’t happen if the ops are too novel to exist in torch (e.g. mamba scan),
• that can’t work if NJTs cause torch.compile errors

So, there’s no choice but to purge them, in exchange for uglier code. A rather sad affair overall.

Optim

#

For the $\mu$P scheme I described in the last post, the params of a model have to be split into groups keyed by

• optim (adam vs muon)
• mup type (first vs hidden vs last vs norms vs mamba vs …)

H-Nets also include an LR Modulation rule (to account for effective batch size of chunks), so we need one extra key:

• hierarchy (s=0,1,2,…)

Since $\uparrow |\text{groups}| \implies \uparrow \text{CPU overhead}$, the CPU overhead of the optimizer is increased a bit by H-Net.

But, in my experience, it does not take much effort to put optim CPU time at ~10% of each train step. I merely

• use dion’s batched muon impl with CUDAGraphs
• apply simple foreach methods to other steps (with some care to exactly match torch impl)

Conclusion

#

After that work, my S2-small.yaml config is primarily CUDA bound:

Emphasis on CUDA-bound, instead of compute bound – the mamba2 layers are still more memory bandwidth bound than compute bound, so MFU at small dims+seqlen is disappointingly low relative to a standard transformer.

Below: ~2/3 total time spent in mamba/dechunk -> ~40% non-matmul time in H-Net for S2-small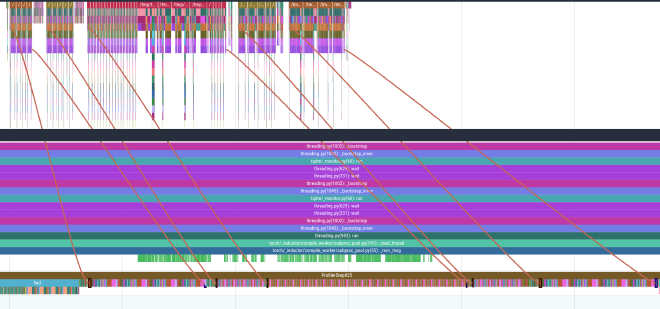

If this lack of tensor core utilization is still unacceptable to you, please provide feedback to the following entities:

• The inventors of Mamba2, for their architectural decisions
• Hardware manufacturers, for providing insufficient wealth to SK Hynix to improve HBM speeds

Otherwise, you can check out the 1-gpu module code here, which is intentionally stripped down for use in external codebases.