H-Net - Parameterization (S≥1)

Previously, I established my bespoke $\mu$P+Muon scheme for llama2 & mamba2.

Now, we arrive at the actual part of the work I care about – optimizing H-Nets across widths.

What could go wrong?

LR Modulation

#

H-Net’s convoluted $\lambda^s = \sqrt{N^\text{GPT}\frac{\prod^S_{i=s}N^i}{\prod^S_{i=0}N^i}\frac{D^S}{D^s}}$ rule is just the application of 2 heuristics:

1. $\eta\propto\frac{1}{\sqrt{D}}$
   • Each hierarchy has a different model dim $D^s$.
2. $\eta\propto\sqrt{\text{batch size}}$
   • Each hierarchy of a H-Net consumes a fraction $\frac{\prod^S_{i=s}N^i}{\prod^S_{i=0}N^i}$ of the bytes
   • $N^\text{GPT}$ is a constant, used in the paper to compare runs with the same bytes per batch. If LR is sweeped, it doesn’t matter.

For my purposes, I remove the $\frac{D^S}{D^s}$ component, as the $\mu$P setup accounts for it.

New modules

#

In addition to the mamba2/transformer/lm blocks, H-Nets have the following extra parameters:

1. routing $W_q$ and $W_k$
2. residual_proj $W_\texttt{res}$ (and bias, but let’s ignore it)
3. pad_dimension (iff $d_s>d_{s-1}$)

Presumably, (1,2) will be trained with Muon, and (3) will be trained with adam.

Pad dim

#

Goombalab does zero init for padding.

Initially, I thought this was bad, as it would violate $||\mathbf h_\ell||_2 = \Theta(\sqrt{d_s})$ on the inputs to deeper hierarchies. But, because the padded input $x_\texttt{pad}$ is only directly used by layers with prenorm, no weight matrix will encounter that violation.

If you did want to match $x_\texttt{pad}$ anyway, you would init pad_dimension as $\sigma\propto 1$. But I think there is little justification for doing so, and it is reasonable to assume the convention that has held since Spacebyte is not significantly detrimental.

In the future, it may be worth switching their cat/slice approach to explicit dim projections between hierarchies. But I am currently unwilling to modify H-Net’s architecture, so I simply treat it as an adam bias and carry on.

Routing module

#

Both $W_q$ and $W_k$ are initialized as the identity matrix.

This logically makes sense – the routing mechanism is a comparison of pairwise $\texttt{cossim}(q_t,k_{t-1})$, so a reasonable place to start is to set $q = k = x$ and compare $x_t\leftrightarrow x_{t-1}$ directly.

A natural question arises: if identity $q$/$k$ are reasonable choices at init, do we even need learnable $W_q$/$W_k$ at all?

Interestingly, there is a prior work from the computer vision space, ToMe, that uses a similar cosine similarity metric between tokens. In that work, they reuse $k$ from each attention layer to determine token selection per layer, and demonstrate that learned $k$ beats using raw $x$ significantly:

So, I can be reasonably confident that,

• pairwise cosine similarity is a good metric for 1D
• at least one learnable matrix is beneficial for selection.

It’s still reasonable to ask if you do need separate $W_q$ and $W_k$. I think the special case of learnable $W_k$ & identity $W_q$ should be no less expressive than H-Net’s original approach. But I leave modification of their architecture to future endevors.

Incidentally, $||\mathbf I_d||_* = 1 = \Theta(\sqrt{\frac{n_\ell}{n_{\ell-1}}})$, so $W_q,W_k$ satisfies the spectral condition with no effort on our part.

It’s possible adding a small amount of orthogonal noise to $W_q,W_k$ at init could improve performance, but I am not willing to test this.

P grads

#

Traditional H-Net defines (for a hierarchy level $s$),

And we’d like to make $\Delta p_t = \mathcal O(1)$ w.r.t. width $D_s$.

Assuming that,

• With non-parametric norms, we have guaranteed $||x_t||_2 = \Theta(\sqrt{d})$.
• With the spectral condition, we have $||q_t||_2 = \Theta(\sqrt{d}) = ||k_t||_2$ as well.
• With no alignment, $q_{t-1}\cdot k_t = \Theta(\sqrt d)$.

We will have $p_t=\Theta(\frac{1}{\sqrt d})$ at init.

And because

We can conclude $\Delta p_t = \langle \frac{\delta p_t}{\delta q_t}, \Delta q_t \rangle = \Theta(1)$

So $\Delta p_t = \Theta(1)$ iff $q_{t-1},k_t$ remains mostly unaligned across widths.

In the median case, that is always true, since a H-Net only “works” iff ~$\frac{N-1}{N}$ of all $t$ positions have $\text{cossim}(q_{t-1},k_t)\lt 0$.

But, in the general case, that does not work, and later we will discuss why.

Residual projection

#

Like pad_dimension, $W_\texttt{res}$ is zero-initialized.

Unlike pad_dimension, this is well-motivated.

From the bible:

One additional detail is that this residual connection is initialized close to 0; earlier versions of H-Net found this to be an important detail, but it may be less important when combined with additional techniques such as LR modulation.

When $W_\texttt{res} = \mathbf 0$, the main network is forced to learn to improve $x_\texttt{dec}$, suppressing easy first-step gains from encoder byte-level prediction improvements alone.

If you use default kaiming uniform init instead, the network never encounters the initial ‘hockey-stick’ ratio loss spike in favor of the main network (higher loss -> more tokens in main net)

So it should be similarly problematic to switch to a $\sigma\propto\frac{1}{\sqrt d}$ init (which both STP and our spectral approximation will use in this $\mathbb R^{d\times d}$ case)

Now, obviously, $||\mathbf 0||_* = 0$, so a zeros init $W_\texttt{res}$ cannot satisfy the spectral condition, and $||\Delta x_\texttt{dec}||_2$ might not be $\Theta(\sqrt{d_s})$.

But it will be the case that $||x_\texttt{dec}||_2=\Theta(\sqrt{d_s})$ at init, due to the main net branch, and empirically this seems OK.

Norms

#

Earlier, I described my use of non-parametric norms in conventional LLMs, where it has a negligible impact on performance.

And, initially, I expected this to hold for H-Net as well, because all of its norms are contained in the Isotropic block, which is equivalent to that of a standard LLaMA architecture.

However, this similarity is actually a programmatic sleight-of-hand. RMSNorms in H-Net do not serve the same purpose as they do in standard pre/post-norm transformer blocks.

While it is true that all norm scales in an $S=0$ H-Net can be subsumed into linear layers, this claim is not true once you start adding hierarchies.

The output norm of an isotropic actually serves 3 distinct roles in a H-Net

1. as a final $\text{LMHead}(\text{RMSNorm}(x))$, in the outermost decoder ($S>0$) OR main network ($S=0$)
   • We could make these trainable via the $\eta_\gamma\propto\frac{1}{\sqrt{d}}$ solution I proposed much earlier, but that is not necessary.
2. as the encoder’s outputs, for the conjoined purposes of
   • routing module stability
   • invariant of each hierarchy starting with $\Theta(1)$ inputs
   • ensuring only $W_\texttt{res}$ decides how much the encoder contributes to $x_\texttt{dec}$
3. to stabilize residual contribution to $x_\texttt{dec}$, in the main network (innermost $s=S-1$) OR decoder ($s\in[1,S-2]$).

Let us focus a bit on case (3).

Both $y_\texttt{enc}$ and $M(...)$ are normalized. The dechunk EMA shrinks variance a bit on average, but not by much.

If $\text{RMS}(W_\texttt{res})$ grows, it is not possible for the outputs of the main net to grow its own RMS to match. Most likely, the main net will start painfully producing gigantic outlier coordinates to pass information out, which will destroy models in the long run.

So, if we want to avoid this, we need to either

• specifically for case (3), make the final norms of each Isotropic layer trainable
• use a linear production to map from deeper to shallow hierarchies, instead of just dim slicing.

I pick the former option. And in this case, to match the update speed of $W_\texttt{res}$, we should use $\eta_\gamma\propto 1$.

TLDR

#

Our first stab at H-Net $\mu P$ adopts the following:

• pad_dimension, residual bias: zeros && adam bias lr
• norm scales: ones init && 0LR OR adam bias lr (only for residual contributing isotropics)
• $W_\texttt{res}$: zeros init and muon update
• $W_q,W_k$: identity init and muon update

Does it work?

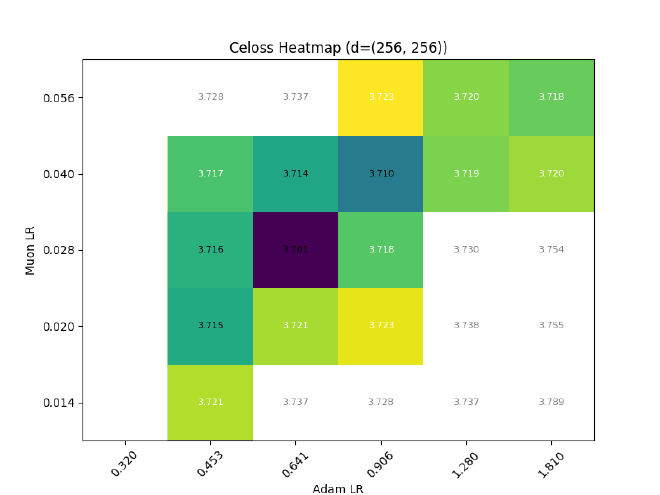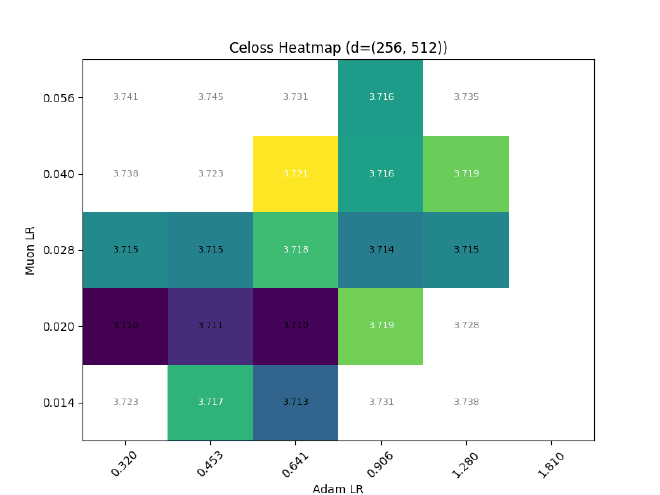
Nope. What gives?

Premise

#

Let’s first establish what is desired from “muP H-Net”.

Given a H-Net of $S$ hierarchies, with model dimensions $D_0\le...\le D_{S-1}$, and fixed batch size / layer count / step count,

1. I should only need to sweep global base values $[\sigma, \eta_\text{muon}, \eta_\text{adam}]$ to achieve reasonably competitive performance (bpb) for fixed base dimensions $d_0,d_1,...,d_{S-1}$
2. The optimal base values should also be optimal for arbitrary $D_0...D_{S-1}$.

Sounds good? It shouldn’t. Here are a few problems:

Compression at Init

#

Consider the following wrong premise:

1. The encoder starts with an output RMSNorm, guaranteeing $y_\texttt{enc}\sim N(0,1)$.
2. The routing module uses identity init, giving $q_t = k_t = y_\texttt{enc} \sim N(0,1)$
3. At init, uncorrelated $q_{t-1},k_t$ should give $\mathbb E[\text{cossim}(q_{t-1},k_t)]\approx 0$,
4. $\therefore$ the base $\sigma$ used has negligible impact on compression ratio at init.

Then, consider the following empirical plot:

The expectation in (3) works when $\sigma$ is small, causing the encoder layers to contribute minimally to $y_\texttt{enc}$ at init, making $\text{L1:L0}$ start off at approximately 1/2.

Conversely, high $\sigma$ + prefix-scan/conv1d causes more correlation out-of-the-box, bringing the starting compression ratio to a negligible value, which generally never goes back up. This dooms all high σ runs && forces HEBO to search for lower $\sigma$ solutions.

I only noticed this extremely late into research, so I never piloted any solutions for it. But

• it should be analytically solvable given the exact encoder dims
• it is ’naturally’ solved-by-accident with forced compression, which gives the main network exposure time

Instability at low step counts

#

In an average small-scale H-Net run, it takes 500+ steps for ratio loss to stabalize close to 1.

That means, that if your $\mu P$ sweeps are done in a very short step regime (I used 1000 steps for baselines), the majority of your run’s updates will be dominated by the starting dynamics of routing stability.

The best hparams under that regime are very unrepresentative of what occurs in ‘real’ H-Nets runs (of $O(100,000)$ steps), where compression factor should be extremely stable.

So, my perspective here is:

• traditional H-Net hparam sweeping is misleading if done with $\text{steps} \lt 5000$
• Ideally, the architecture should be modified to have stable token consumption at all steps.

Infeasibility of consistent bsz

#

It is not possible to make a traditional H-Net consume the same number of tokens per step. The model decides how many tokens the inner nets get to see; traditional fixed batch size mup is intractable with H-Net.

In a simple width transfer test ($D_{0,1}={256,256}\rightarrow{256,512}$), the learning trajectory of routing selection will change, which changes the tokens visible to the inner main network, which butterfly-effects the entire training run:

Now, to be clear, these aren’t “huge” instabilities. But it definitely destroys any possibility of direct hparam transfer, without accounting for the shift in routing choices w.r.t. width.

And if you’ve read my Intuitions, you’ll know that it’s wrong to try to fight compression ratio in this regard – the model deviates from target compression when it’s better for performance.

P grads (again)

#

Earlier, I claimed:

So $\Delta p_t = \Theta(1)$ iff $q_{t-1},k_t$ remain mostly unaligned across widths… in most cases, they should remain unaligned as our H-Net is only “working” iff $\text{cossim}(...)<0$ for $\frac{N-1}{N}$ of $t$ positions.

But this is a self-defeating premise. Iff H-Nets are really true dynamic tokenizers, then you would expect increases in model capacity to adjust the alignment of $q_{t-1},k_t$, to enable a shift in chunk size towards what’s optimal.

So,

🙁

Proposed solutions

#

I roughly see 3 ‘classes’ of solutions for the above:

1. Forced compression ratio
2. LR adjustments
3. Pretrained encoders

Here’s how they work.

Forced compression

#

Even if you empirically understand ratio loss should not be fucked with, it’s tempting to try.

Typically, sweeps over global LR parameters directly adjust the curvature of the hockey-stick at the start of a run, like this:

• lower muon LR -> slower $W_{q,k}$ updates -> longer dragged hockey stick (which is lowest first valley & highest first peak)
• higher adam LR also causes the same thing. not very sure why

So, that’s very bad for short run equivalence. What can we do?

Obvious bad approach

#

A natural first question to ask is if any of this even matters. Is this instability really what’s stopping $\mu$P?

It’s quite easy to force the issue on this particular task – just hardcode compression ratio:

@@ -82,9 +97,15 @@ class RoutingModule(nn.Module):
         q_flat = QProjPadded.apply(r_flat, self.q_proj_layer.weight, k_flat, r_cu)
         cos_sim = F.cosine_similarity(q_flat, k_flat, dim=-1)
         p_flat = (.5-cos_sim/2).clamp(.0,1.)
-        b_flat = p_flat >= 0.5
+        if self.break_causality:
+            with torch.no_grad():
+                ratio = (self.break_causality-1)/self.break_causality
+                kth = p_flat.kthvalue(int(ratio*p_flat.numel())).values
+                dist.all_reduce(kth)
+                self.thresh.copy_(kth)
+        b_flat = p_flat >= self.thresh
         p_select_cu = F.pad(b_flat.cumsum(0),(1,0))[r_cu]
-        return p_flat, b_flat, p_select_cu
+        return p_flat, b_flat, p_select_cu, p_flat >= .5

Now, obviously, this breaks causality, and cannot ever be used in a real H-Net run.

But for research purposes, it helps to answer the question of what is crippling $\mu$Transfer.

“Yes”, in the sense that optimal LR doesn’t drift away.

“No”, because the results are fucked – loss increases with width, instead of the other way around…

More bad approaches

#

I cycled through many bad ideas in pursuit of init stability. Here are some of them:

Deepseek-inspired loss free

Inspired by Deepseek, I implement the following simple alternative to routing loss:

class RoutingModuleAuxFree(RoutingModule):
    def __init__(self, d: int):
        super().__init__(d)
        with torch.device("cuda"):
            self.register_buffer("thresh", torch.tensor(0.5))
            self.register_buffer("err_ema", torch.tensor(0.))

    def forward(self, r_flat: TT, r_cu: TT):
        k_flat = self.k_proj_layer(r_flat)
        q_flat = QProjPadded.apply(r_flat, self.q_proj_layer.weight, k_flat, r_cu)
        cos_sim = F.cosine_similarity(q_flat, k_flat, dim=-1)
        p_flat = (.5-cos_sim/2).clamp(.0,1.)
        b_flat = p_flat >= self.thresh # only this is replaced
        p_select_cu = F.pad(b_flat.cumsum(0),(1,0))[r_cu]
        return p_flat, b_flat, p_select_cu

    def update_thresh(self, n: float, b_flat: TT, *, u: float=1e-3, beta: float=0.95):
        # obtain global metrics for numel_flat and numel_select
        numel = torch.stack([
            torch.scalar_tensor(b_flat.numel(),device='cuda'),
            b_flat.sum()
        ])
        dist.all_reduce(numel)

        # calc deviation from target compression, update ema of error
        target = numel[0] * (1/n)
        err_cur = numel[1] - target
        self.err_ema.lerp_(err_cur, 1-beta)

        # update the threshold based of ema's sign (similar to deepseek)
        step = u*torch.sign(self.err_ema)
        self.thresh.add_(step).clamp_(.1,.9) # clamp to avoid failed runs

In a single test run, this both (A) made compression factor more stable and (B) provided no difference in loss:

Does it work in the general case?

No, because I clamp updates within [.1,.9] for numerical stability, and it is easy for bad runs to increase/decrease $p_t$ far beyond that.

With infinite precision, balancing should ‘work’. But:

1. actual bf16 will quickly saturate and cause routing to become increasingly volatile
2. you don’t actually want to do this for the aforementioned reasons of respecting H-Nets that override ratio loss

​

Balanced loss weight

Another obvious approach is to grow the magnitude of the routing loss grads together with the influence of celoss.

This can be achieved with a similar scheme that balances $\mathcal L_\text{ratio}$’s $\alpha$ directly, instead of adjusting routing threshold:

    def ratio_loss(self, b_flat: TT, p_flat: TT):
        f = b_flat.mean(dtype=torch.float32)
        g = p_flat.mean(dtype=torch.float32)

        drop_experts = self.n*(1-f)*(1-g) / (self.n-1)
        keep_expert = self.n*f*g
        loss = self.alpha.clone() * (keep_expert + drop_experts)
        
        # update loss weight alpha by preferred direction
        if self.diff_ema is not None:
            with torch.no_grad():
                diff = f-self.n*b_flat.numel()
                self.diff_ema.lerp_(diff, 0.95)
                # positive diff -> too many tokens -> increase ratio loss
                step = 0.01*(self.diff_ema).sign()
                self.alpha.add_(step).clamp_(0.01,100)
        return loss

But it does not improve results (1e17 also crashed a bit):

And, once again: this is because forcing a model to do more compression is bad

Both of them were failures, unlike the next idea:

Not wrong approach

#

One basic scheme to force compression stability is to adjust the >=0.5 threshold based on previous step statistics:

    @torch.no_grad()
    def update_thresh(self, N: int, p_flat: TT, *, cutoff: int=1000):
        import math
        ratio = (N-1)/N
        kth = p_flat.kthvalue(int(ratio*p_flat.numel())).values
        # interp from cos(0) -> cos(pi/2)
        w = math.cos(math.pi * self.step.item() / cutoff / 2)
        t = kth.lerp(torch.scalar_tensor(.5,device=p_flat.device), 1-w)
        dist.all_reduce(t)
        self.thresh.copy_(t)
        self.step.add_(1)

This has to be done with a distinction between “fake” and “real” $b_t$, to still give ratio loss / STE the same routing signals:

@@ -82,9 +97,10 @@ class RoutingModule(nn.Module):
         q_flat = QProjPadded.apply(r_flat, self.q_proj_layer.weight, k_flat, r_cu)
         cos_sim = F.cosine_similarity(q_flat, k_flat, dim=-1)
         p_flat = (.5-cos_sim/2).clamp(.0,1.)
-        b_flat = p_flat >= 0.5
+        b_flat = p_flat >= self.thresh
         p_select_cu = F.pad(b_flat.cumsum(0),(1,0))[r_cu]
-        return p_flat, b_flat, p_select_cu
+        return p_flat, b_flat, p_select_cu, p_flat >= .5

@@ -219,14 +238,17 @@ class HNet(nn.Module):
         if self.is_innermost: return self.main_network(x_flat, flat_cu, msl)[...,:d_orig],[]
 
         r_flat = self.encoder(x_flat, flat_cu, msl)
-        p_flat, b_flat, select_cu = self.routing_module(r_flat, flat_cu)
+        p_flat, b_flat, select_cu, b_flat_unbiased = self.routing_module(r_flat, flat_cu)
 
         select_stats_gpu = torch.stack([select_cu.diff().max(), select_cu[-1]])
         with least_blocking_d2h(select_stats_gpu) as select_stats_cpu:
-            ratio_loss = self.ratio_loss(b_flat, p_flat) if torch.is_grad_enabled() else 0
-            c_flat = torch.where(b_flat, p_flat, 1-p_flat)[...,None]
+            if torch.is_grad_enabled():
+                ratio_loss = self.ratio_loss(b_flat_unbiased, p_flat)
+                if self.init_stable: self.routing_module.update_thresh(self.n, p_flat)
+            else: ratio_loss = 0
+            c_flat = torch.where(b_flat_unbiased, p_flat, 1-p_flat)[...,None]
             residual = self.residual_proj(r_flat)

Do that, and compression at init will become much more stable without changing behavior after the step threshold (much)

Note that, in the above runs,

• logs happen every 5 iters, so the cutoff for regressing to original H-Net is at “step”=200.
• The green line is with the diff above; the yellow line is a separate case where I move up update_thresh to be causality-breaking, to ~no change.

In any case, the intervention causes the hockey-stick to flatten out:

But, problematically, there is still a wide variation of compression in the long run:

As per usual, lower muon LR -> slower ascent of compression to target 0.2. This causes all of the runs below a certain muon LR to strongly underperform:

So, mild force compression is not enough. What’s next?

LR adjustment

#

Two subideas here.

Segregated routing LR

#

One reasonable problem you might expect from tying $W_q,W_k$ LR to the LR of all other matrices, is that minute improvements in learning speed to the main network in general may end up overshadowed by the router ‘adversarially’ learning to route worse for the main network.

So, having a separate LR group for them (and other routing-related parameters like $W_\texttt{res},\gamma_m$) may help to stabalize the search space for best LR of other parameters.

Of course, this doesn’t help if optimal hparams aren’t width invariant to begin with, but you could imagine this helping after that problem gets solved.

Dynamic LR modulation

#

Instead of the fixed $N$-based LR modulation rule, we could dynamically adjust each hierarchy’s LR based on the active number of tokens seen.

Arguably, doing so would be more principled than the static LR modulation approach based on target compression factor.

But I don’t bother attempting this, as it’s highly unlikely this adjustment will fix anything, given the variation in batch size (with the thresh update trick) is on the order of ±10%.

Pretrained encoder

#

If learning a good chunk mechanism at init is a fundamental issue, why not just use a pretrained encoder+routing?

To be specific, you would:

• load all weights above a certain hierarchy level – including $W_\text{res},W_\text{emb},W_\text{out}$ – from a pretrained H-Net checkpoint
• freeze or otherwise very gently warmup those weights for many steps (as the decoder provides strong language modelling ootb)

Sketch effort

Let’s say you want to take cartesia’s stage1_XL encoder, and use it to $\mu$P to a reasonably mid-sized LLM.

You would start by sweeping hparams with a $D=[1024,1024]$ model, which:

1. copies prior work for best mamba2/transformer $\mu$P scheme
2. uses the scheme above for other H-Net modules
3. is warmed up with cosine-decayed threshold tracking.
4. loads stage1_XL’s weights for the enc/dec, and keeps them frozen.

Then, with those hparams, you would expand to larger $D_1$.

Does that work?

Well, no, because I used a parametric output norm, which predictably causes leftwards $\eta_\text{adam}$ drift under my setup. But this should be fixable if you replace the norm scale with a down projection instead.

And sure, some variant of that idea probably works. But this is not a desirable outcome.

The whole point of H-Net is to provide end-to-end hierarchical language modelling, and to avoid regressing towards multistage training pipelines that complicate the research process.

Nonetheless, it seems to be the simplest strategy to square the circle of wanting dynamic tokenizers & wanting $\mu$P. So I make the following repulsive recommendation to future practitioners:

Conclusions

#

1. End-to-end H-Nets are a poor fit for $\mu$P.
2. Although ugly, separate ‘pretrained tokenizers’ will work.

Future researchers may consider investigating the following:

• Finding errors in the above text to enable $\mu$transfer with end-to-end H-Nets
• Taking inspiration from other generative modalities on how to best balance enc/dec vs main network compute
• Emailing support@cartesia.ai for help