Why reduction precision matters

In torch’s FSDP/FSDP2 MixedPrecision APIs, there’s a reduce_dtype config flag:

reduce_dtype (Optional[torch.dtype]): This specifies the dtype for
    gradient reduction (i.e. reduce-scatter or all-reduce). If this is
	``None`` but ``param_dtype`` is not ``None``, then the reduction
    uses the compute dtype. This can be used to run gradient reduction
    in full precision while using low precision for compute. If also
    gradient reduction is disabled via :meth:`set_requires_gradient_sync`,
    then FSDP will accumulate gradients using ``reduce_dtype``.
    (Default: ``None``)

Why does it exist? Does it even matter? What do people typically use?

Common usage

#

A typical application of FSDP/2 looks like this:

m = Model(...) # <-- some model w/ fp32 params
m = FullyShardedDataParallel(m, ..., mixed_precision=MixedPrecision(bf16))
m(x).backward() # <-- will sync grads as bf16

m = Model(...) # <-- some model w/ fp32 params
fully_shard(m, mp_policy=MixedPrecisionPolicy(param_dtype=bf16))
m(x).backward() # <-- will sync grads as bf16

Does that make it a sane default? Maybe. But strangely, torchtitan, another PyTorch project, has hardcoded their reduction dtype to fp32. So maybe it doesn’t work?

…

Conversely, in pure DDP training, the situation is flipped. Most DDP trainers still apply autocast for mixed precision, instead of the obscure _MixedPrecision API that was implemented 2 years ago. Note that autocast doesn’t communicate in low precision in the absence of specific communication hooks, so most users of DDP will syncronize gradients in single precision, regardless of whether they mean to:

# Typical DDP usage
m = Model(...) # <-- some model w/ fp32 params
m = DistributedDataParallel(m)
with torch.autocast("cuda", bfloat16):
  m(x).backward() # <-- will sync grads via fp32

# It's possible to do the following, but most people don't:
m.register_comm_hook(dist.group.WORLD, bf16_compress_hook)
with torch.autocast("cuda", bfloat16):
  m(x).backward() # <-- will sync grads via bf16

## Atypical DDP usage; implemented almost 2 years ago but ~nobody uses it
m = Model(...) # <-- some model w/ fp32 params
replicate(m, mixed_precision=_MixedPrecision(param_dtype=bfloat16)) 
m(x).backward() # <-- will sync grads as bf16

So, basically, the average PyTorch user doesn’t give a shit and will sync in whatever precision PyTorch defaults to on a specified parallelism scheme.

Is that bad?

Who even cares?

#

To be clear, when discussing the role of precision in gradient reduction,

• we are not talking about the precision of the compute kernels used in the backward pass (which will be bf16/fp16 either way),
• nor are we discussing the storage format used for local gradients (which matches master weights precision, which should be fp32).

The only difference we’re talking about is an up/down cast in-between a distributed sum:

# for educational purposes, I'm only showing the compute involved
# in a reduction, rather than the distributed collectives
# that would actually be used in torch.

# list of bf16/fp16 grads from all GPUs
all_gpu_grads: list[Tensor] = [...]
final_grad_half_reduce = sum(all_gpu_grads).float() # <-- storage dtype always fp32
final_grad_fp32_reduce = sum(x.float() for x in all_gpu_grads) # <-- sum in fp32
divergence = final_grad_half_reduce - final_grad_fp32_reduce 

# see torch/distributed/fsdp/_fully_shard/_fsdp_collectives.py:foreach_reduce if you want a real look

When I first expressed this information to a fellow PyTorch user, his first reaction was denial that the premise should even matter:

if the stuff u r adding is alr bf16 then how does adding in fp32 works […] even if u do the addition in fp32, it wont increase any precision

Fair enough, right? Why the fuck should this even matter at all. After all,

Isn’t the sum identical?

#

Intuition says that,

a = torch.tensor(..., dtype=torch.bfloat16)
b = torch.tensor(..., dtype=torch.bfloat16)

assert a+b == (a.float()+b.float()).bfloat16()

should be true – any accuracy obtained by the higher precision sum on the right-hand-side should be eliminated by the subsequent bf16 cast.

This is generally true in the 2-sum case. Unfortunately, it’s not hard to come up with a counter-example if you allow for 3 or more elements in the sum:

>>> a,b,c = [torch.tensor(x).bfloat16() for x in (1e7, 1.0, -1e7)]
>>> (a+b+c).item()
0.0
>>> ((a.float() + b.float() + c.float()).bfloat16()).item()
1.0

In general, \(A_\text{bf16} + B_\text{bf16} + C_\text{bf16} \ne (A_\text{fp32} + B_\text{fp32} + C_\text{fp32})_\text{bf16}\).

Okay, but what about the real world?

#

The 3-sum case is an unrealistic toy problem: with two values of very large magnitude, and one of very small scale.

What does an actual gradient look like? I’ve no idea in the general case, but let’s say for simplicity that every coordinate in a gradient tensor \(w \sim N(0,\sigma^2)\). Given \(R\) GPUs, an NCCL allreduce AVG will usually compute: $$ \sum_{r=0}^R (w_r/R) $$ That is to say, the allreduce can underflow, but will never overflow. There are edge cases where torch will do some pre-scaling, but I don’t really care about them.

To model the divergence in half precision vs full precision reductions, I created a simple script to plot the variance of the difference between a hypothetical bf16 ring-reduce vs an fp32 ring-reduce:

import torch

def pow2range(start, stop, base=1.0):
    return [base * (2 ** i) for i in range(start, stop + 1)]

BS = 4096
grad_stds = pow2range(-8, -4)  # approx 0.004 ~ 0.0625
world_sizes = [int(R) for R in pow2range(1, 10)]  # 2..=1024

# Simulate reductions
std_of_diff = {std: [] for std in grad_stds}
with torch.device('cuda'):
    for std in grad_stds:
        for R in world_sizes:
            w = torch.normal(0.0, std, (R, BS), dtype=torch.bfloat16)
            o_bf16 = sum(v for v in w/R)
            o_fp32 = (w/R).sum(dim=0)  # equivalent to float().sum().bfloat16()
            diff_std = (o_bf16 - o_fp32).std().item()
            std_of_diff[std].append(diff_std)

Here are the results:

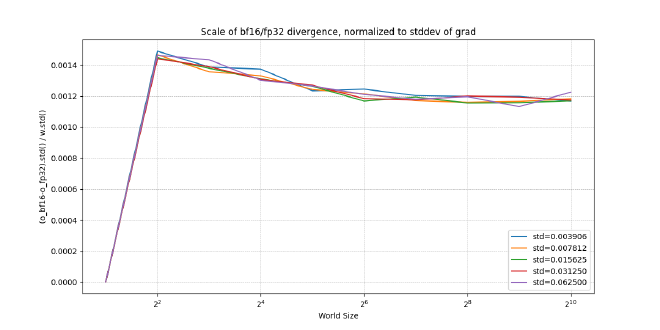
As you can see, the stddev did not increase with scale. As I was not expecting these results, and am unable to further explain them, I will put up a semantic stopsign for myself here and end the blogpost.

Conclusion

#

I don’t understand why reduction precision matters.