In the previous section, we saw the collective communication process using ring allreduce as an example. However, as the number of GPUs used in training tasks expands, ring allreduce’s latency grows linearly. To address this issue, NCCL introduced the tree algorithm, specifically the double binary tree.
double binary tree#
The naive tree algorithm constructs all machine nodes into a binary tree, supporting broadcast, reduce, and prefix sum operations. Suppose a root node needs to broadcast a message M to all nodes. The root sends M to its child nodes, and all other nodes forward M to their children upon receiving it. Leaf nodes only receive M since they have no children. This process can split M into k blocks, enabling pipelining.
However, this naive algorithm has a problem: leaf nodes only receive data without sending any, thus utilizing only half of the bandwidth. To solve this, MPI proposed the double binary tree algorithm. With N nodes in total, MPI constructs two N-sized trees T1 and T2. The intermediate nodes in T1 are leaf nodes in T2. T1 and T2 run simultaneously, each handling half of message M, allowing full utilization of bidirectional bandwidth on each node. Here’s an example with ten machines:
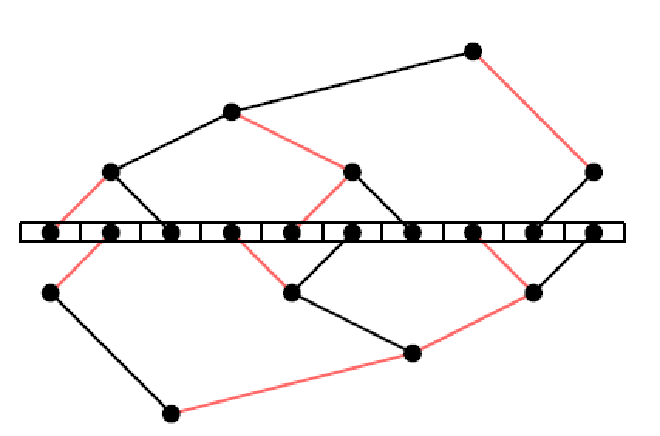
Figure 1#
While T1’s construction will be explained later, T2 can be constructed in two ways: shift (shifting ranks left by one position, e.g., rank10 becomes rank9) or mirror (mirroring rank numbers, e.g., rank0 becomes rank9). The shift method results in identical tree structures, while mirror creates symmetrical trees but only works with an even number of machines.
As shown in Figure 1, T1 and T2’s edges can be colored red or black, yielding these properties:
- No node connects to parent nodes with the same color edges in T1 and T2
- No node connects to child nodes with the same color edges
Following these properties, the workflow involves receiving data from parent nodes and sending previously received data to child nodes at each step, alternating between red edges (even steps) and black edges (odd steps), enabling simultaneous send and receive operations.
nccl tree#
NCCL’s tree is used only between nodes, with nodes internally forming a chain. Version 2.7.8 uses NCCL_TOPO_PATTERN_SPLIT_TREE pattern. For example, with 4 machines and 32 cards, T1 looks like this (T2 will be discussed later):
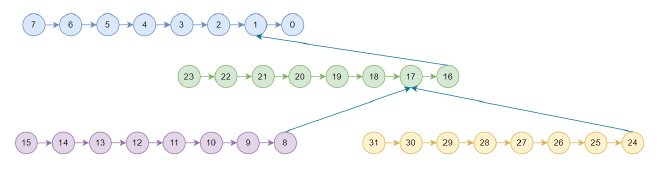
Figure 2#
Since allreduce can be split into reduce and broadcast processes, NCCL tree allreduce first performs reduce (upward phase) from rank15, rank31, rank23, rank7 to rank0, then broadcasts (downward phase) from rank0 to all cards.
tree search#
As mentioned, nodes form internal chains, so intra-node tree search is similar to ring search, using NCCL_TOPO_PATTERN_SPLIT_TREE pattern and executing ncclTopoCompute.
struct ncclTopoGraph treeGraph;
treeGraph.id = 1;
treeGraph.pattern = NCCL_TOPO_PATTERN_SPLIT_TREE;
treeGraph.crossNic = ncclParamCrossNic();
treeGraph.collNet = 0;
treeGraph.minChannels = 1;
treeGraph.maxChannels = ringGraph.nChannels;
NCCLCHECK(ncclTopoCompute(comm->topo, &treeGraph));
NCCLCHECK(ncclTopoPrintGraph(comm->topo, &treeGraph));
In ncclTopoCompute, search parameters are set with backToFirstRank = -1 and backToNet = 1 for NCCL_TOPO_PATTERN_SPLIT_TREE.
ncclResult_t ncclTopoSearchParams(struct ncclTopoSystem* system, int pattern, int* backToNet, int* backToFirstRank) {
if (system->nodes[NET].count) {
if (pattern == NCCL_TOPO_PATTERN_RING) *backToNet = system->nodes[GPU].count-1;
else if (pattern == NCCL_TOPO_PATTERN_TREE) *backToNet = 0;
else *backToNet = 1;
if (pattern == NCCL_TOPO_PATTERN_SPLIT_TREE_LOOP) *backToFirstRank = system->nodes[GPU].count-1;
else *backToFirstRank = -1;
} else {
*backToNet = -1;
if (pattern == NCCL_TOPO_PATTERN_RING || pattern == NCCL_TOPO_PATTERN_SPLIT_TREE_LOOP) *backToFirstRank = system->nodes[GPU].count-1;
else *backToFirstRank = -1;
}
return ncclSuccess;
}
This results in the following tree (assuming only one tree is found for simplicity):
NET/0 GPU/0 GPU/1 GPU/2 GPU/3 GPU/4 GPU/5 GPU/6 GPU/7 NET/0
Connecting the tree#
ncclResult_t ncclTopoPreset(struct ncclComm* comm,
struct ncclTopoGraph* treeGraph, struct ncclTopoGraph* ringGraph, struct ncclTopoGraph* collNetGraph,
struct ncclTopoRanks* topoRanks) {
int rank = comm->rank;
int localRanks = comm->localRanks;
int nChannels = comm->nChannels;
for (int c=0; c<nChannels; c++) {
struct ncclChannel* channel = comm->channels+c;
channel->treeUp.up = -1;
for (int i=0; i<NCCL_MAX_TREE_ARITY; i++) channel->treeUp.down[i] = -1;
channel->treeDn.up = -1;
for (int i=0; i<NCCL_MAX_TREE_ARITY; i++) channel->treeDn.down[i] = -1;
}
...
}
Then execute ncclTopoPreset. As mentioned above, the tree allreduce process is divided into upward and downward phases. Therefore, we can see that each channel has two trees: treeUp and treeDn, representing upward and downward phases. Both treeUp and treeDn actually correspond to the same tree, such as T1. However, since treeUp and treeDn are identical, newer versions of nccl only maintain one data structure, so in the following introduction, we only need to focus on treeUp.
treeDn.up represents the parent node, initialized here as -1. treeDn.down[i] represents child nodes, also initialized as -1. NCCL_MAX_TREE_ARITY indicates the maximum number of child nodes. Since it’s a binary tree plus one intra-machine child node, there can be at most three child nodes, so NCCL_MAX_TREE_ARITY equals 3.
ncclResult_t ncclTopoPreset(struct ncclComm* comm,
struct ncclTopoGraph* treeGraph, struct ncclTopoGraph* ringGraph, struct ncclTopoGraph* collNetGraph,
struct ncclTopoRanks* topoRanks) {
int rank = comm->rank;
int localRanks = comm->localRanks;
int nChannels = comm->nChannels;
for (int c=0; c<nChannels; c++) {
...
int* ringIntra = ringGraph->intra+c*localRanks;
int* treeIntra = treeGraph->intra+c*localRanks;
int* collNetIntra = collNetGraph->intra+c*localRanks;
for (int i=0; i<localRanks; i++) {
...
if (treeIntra[i] == rank) {
int recvIndex = 0, sendIndex = treeGraph->pattern == NCCL_TOPO_PATTERN_TREE ? 0 : 1;
int prev = (i-1+localRanks)%localRanks, next = (i+1)%localRanks;
// Tree loop always flows in the same direction. Other trees are symmetric, i.e.
// up/down go in reverse directions
int sym = treeGraph->pattern == NCCL_TOPO_PATTERN_SPLIT_TREE_LOOP ? 0 : 1;
// Down tree is common
topoRanks->treeDnRecv[c] = treeIntra[recvIndex];
topoRanks->treeDnSend[c] = treeIntra[sendIndex];
channel->treeDn.up = treeIntra[prev];
channel->treeDn.down[0] = treeIntra[next];
// Up tree depends on the pattern
topoRanks->treeUpRecv[c] = sym ? topoRanks->treeDnSend[c] : topoRanks->treeDnRecv[c];
topoRanks->treeUpSend[c] = sym ? topoRanks->treeDnRecv[c] : topoRanks->treeDnSend[c];
channel->treeUp.down[0] = sym ? channel->treeDn.down[0] : channel->treeDn.up ;
channel->treeUp.up = sym ? channel->treeDn.up : channel->treeDn.down[0];
}
...
}
...
}
// Duplicate channels rings/trees
struct ncclChannel* channel0 = comm->channels;
struct ncclChannel* channel1 = channel0+nChannels;
memcpy(channel1, channel0, nChannels*sizeof(struct ncclChannel));
return ncclSuccess;
}
Then initialize treeUp based on the intra-machine searched chain. Set up as prev, down[0] as next, treeUpRecv as 1 (indicating the current machine will use rank with localrank 1 to execute recv), and treeUpSend as 0 (indicating the current node will use rank with localrank 0 to execute send). The structure is shown below, with arrows pointing to up, yellow indicating treeUpSend, and green indicating treeUpRecv.
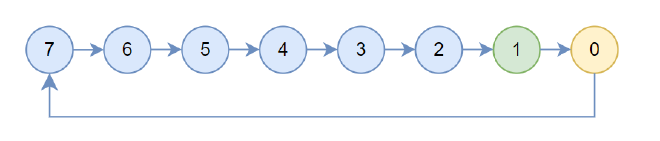
Figure 3#
Finally, duplicate the channel, with nChannels being 1. After duplication, there are two channels total. As we’ll see later, channel0 corresponds to T1, and channel1 corresponds to T2.
After Preset, execute global allgather to get information from all nodes, then execute Postset to complete the global tree connection.
First, flatten each rank’s treeUpRecv and treeUpSend into a single array.
ncclResult_t ncclTopoPostset(struct ncclComm* comm, int* firstRanks, struct ncclTopoRanks** allTopoRanks, int* rings) {
// Gather data from all ranks
int *ringRecv, *ringSend, *ringPrev, *ringNext, *treeUpRecv, *treeUpSend, *treeDnRecv,*treeDnSend;
int nranks = comm->nRanks;
int nChannels = comm->nChannels;
...
NCCLCHECK(ncclCalloc(&treeUpRecv, nranks*MAXCHANNELS));
NCCLCHECK(ncclCalloc(&treeUpSend, nranks*MAXCHANNELS));
NCCLCHECK(ncclCalloc(&treeDnRecv, nranks*MAXCHANNELS));
NCCLCHECK(ncclCalloc(&treeDnSend, nranks*MAXCHANNELS));
for (int i=0; i<nranks; i++) {
for (int c=0; c<nChannels;c++) {
...
treeUpRecv[c*nranks+i] = allTopoRanks[i]->treeUpRecv[c];
treeUpSend[c*nranks+i] = allTopoRanks[i]->treeUpSend[c];
...
}
}
NCCLCHECK(connectTrees(comm, treeUpRecv, treeUpSend, treeDnRecv, treeDnSend, firstRanks));
...
}
Then execute connectTrees
static ncclResult_t connectTrees(struct ncclComm* comm, int* treeUpRecv, int* treeUpSend, int* treeDnRecv, int* treeDnSend, int* firstRanks) {
const int nChannels = comm->nChannels, nNodes = comm->nNodes, node = comm->node;
int* indexesSend, *indexesRecv;
NCCLCHECK(ncclCalloc(&indexesSend, nNodes));
NCCLCHECK(ncclCalloc(&indexesRecv, nNodes));
// Compute tree depth. Not an exact value but a good approximation in most
// cases
int depth = comm->nRanks/nNodes - 1 + log2i(nNodes);
int u0, d0_0, d0_1, u1, d1_0, d1_1;
NCCLCHECK(ncclGetDtree(nNodes, node, &u0, &d0_0, &d0_1, &u1, &d1_0, &d1_1));
...
}
First, use ncclGetDtree to build a double binary tree structure based on the number of nodes. u0 is the current node’s parent in T1, d0_0 and d0_1 are the current node’s left and right children in T1. Similarly, u1, d1_0, and d1_1 are the parent node and left/right children in T2.
In ncclGetDtree, first build T1’s structure through ncclGetBtree, then obtain T2 through shift or mirror. However, there seems to be some issues in version 2.7.8: shift is used for even number of machines, mirror for odd numbers. As mentioned earlier, mirror method only works well with even number of machines; otherwise, some nodes would be leaf nodes in both trees, leading to poor performance. This has been fixed in newer versions. We’ll explain the subsequent logic assuming mirror for even nodes and shift for odd nodes.
ncclResult_t ncclGetDtree(int nranks, int rank, int* s0, int* d0_0, int* d0_1, int* s1, int* d1_0, int* d1_1) {
// First tree ... use a btree
ncclGetBtree(nranks, rank, s0, d0_0, d0_1);
// Second tree ... mirror or shift
if (nranks % 2 == 0) {
// shift
int shiftrank = (rank-1+nranks) % nranks;
int u, d0, d1;
ncclGetBtree(nranks, shiftrank, &u, &d0, &d1);
*s1 = u == -1 ? -1 : (u+1) % nranks;
*d1_0 = d0 == -1 ? -1 : (d0+1) % nranks;
*d1_1 = d1 == -1 ? -1 : (d1+1) % nranks;
} else {
// mirror
int u, d0, d1;
ncclGetBtree(nranks, nranks-1-rank, &u, &d0, &d1);
*s1 = u == -1 ? -1 : nranks-1-u;
*d1_0 = d0 == -1 ? -1 : nranks-1-d0;
*d1_1 = d1 == -1 ? -1 : nranks-1-d1;
}
return ncclSuccess;
}
Then use ncclGetBtree to build T1. The comments are very detailed. First find the lowest non-zero bit (lowbit) in the current node’s binary number. Taking the example of 14 machines from the comments:
For parent nodes: If node binary is like xx01[0], where 1 represents lowbit, [0] represents consecutive zeros, xx can be any high bits, if xx10[0] < nranks, then parent node is xx10[0] according to 1.1. If xx10[0] >= nranks, then parent node is xx00[0]. If node binary is like xx11[0], then parent node is xx10[0]. For child nodes, current node is like xx10[0]: For left child node, since it must be smaller than the current node, it must be transformed from rule 1.1, so just reverse to xx01[0]. If lowbit is 0, then left child is -1. For right child node, which is larger than current node, for case 1.3 it’s easy - just set lowbit-1 bit to 1, i.e., xx11[0]. If xx11[0] >= nranks, it’s case 1.2, where we don’t know the right child’s lowbit, so must check bit by bit from left to right.
Then construct T2 through shift or mirror method, which won’t be elaborated further.
/* Btree which alternates leaves and nodes.
* Assumes root is 0, which conveniently builds a tree on powers of two,
* (because we have pow2-1 ranks) which lets us manipulate bits.
* Find first non-zero bit, then :
* Find the parent :
* xx01[0] -> xx10[0] (1,5,9 below) or xx00[0] if xx10[0] is out of bounds (13 below)
* xx11[0] -> xx10[0] (3,7,11 below)
* Find the children :
* xx10[0] -> xx01[0] (2,4,6,8,10,12) or -1 (1,3,5,7,9,11,13)
* xx10[0] -> xx11[0] (2,4,6,8,10) or xx101[0] (12) or xx1001[0] ... or -1 (1,3,5,7,9,11,13)
*
* Illustration :
* 0---------------8
* ______/ \______
* 4 12
* / \ / \
* 2 6 10 \
* / \ / \ / \ \
* 1 3 5 7 9 11 13
*/
ncclResult_t ncclGetBtree(int nranks, int rank, int* u, int* d0, int* d1) {
int up, down0, down1;
int bit;
for (bit=1; bit<nranks; bit<<=1) {
if (bit & rank) break;
}
if (rank == 0) {
*u = -1;
*d0 = nranks > 1 ? bit >> 1 : -1;
*d1 = -1;
return ncclSuccess;
}
up = (rank ^ bit) | (bit << 1);
if (up >= nranks) up = (rank ^ bit);
*u = up;
int lowbit = bit >> 1;
// down0 is always within bounds
down0 = lowbit == 0 ? -1 : rank-lowbit;
down1 = lowbit == 0 ? -1 : rank+lowbit;
// Make sure down1 is within bounds
while (down1 >= nranks) {
down1 = lowbit == 0 ? -1 : rank+lowbit;
lowbit >>= 1;
}
*d0 = down0; *d1 = down1;
return ncclSuccess;
}
At this point, the double binary tree construction is complete. Taking 4-machine scenario as example, the constructed tree is shown below, with blue representing T1 and green representing T2. This differs from the original paper in that T2’s structure should be symmetrical to T1, though this doesn’t affect functionality.
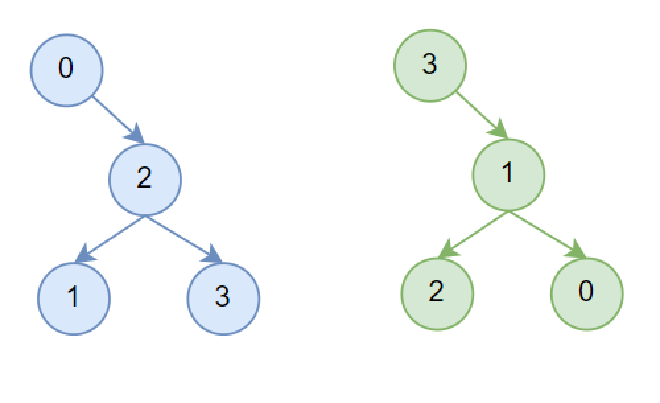
Figure 4#
Now we have the intra-machine connections from Figure 3 and inter-machine structure from Figure 4. connectTrees will next complete the inter-machine connections shown in Figure 2.
Here channel0 is the searched channel, and channel1 is the copy of channel0. channel0 corresponds to T1, channel1 to T2. treeUpSend stores each rank’s send rank from the searched channel (yellow nodes in Figure 3). getIndexes retrieves each node’s send rank into indexsSend.
static ncclResult_t connectTrees(struct ncclComm* comm, int* treeUpRecv, int* treeUpSend, int* treeDnRecv, int* treeDnSend, int* firstRanks) {
...
for (int c=0; c<nChannels; c++) {
struct ncclChannel* channel0 = comm->channels+c;
struct ncclChannel* channel1 = channel0+nChannels;
NCCLCHECK(getIndexes(treeUpSend+c*comm->nRanks, indexesSend, nNodes, firstRanks));
NCCLCHECK(getIndexes(treeUpRecv+c*comm->nRanks, indexesRecv, nNodes, firstRanks));
NCCLCHECK(openRing(&channel0->treeUp, comm->rank, indexesSend[node]));
NCCLCHECK(openRing(&channel1->treeUp, comm->rank, indexesSend[node]));
int root = indexesSend[node];
if (indexesSend[node] == comm->rank) NCCLCHECK(setTreeUp(&channel0->treeUp, &channel1->treeUp, indexesRecv, u0, u1));
if (indexesRecv[node] == comm->rank) NCCLCHECK(setTreeDown(&channel0->treeUp, &channel1->treeUp, indexesSend, d0_0, d0_1, d1_0, d1_1));
...
channel0->treeUp.depth = channel1->treeUp.depth = depth;
}
free(indexesSend);
free(indexesRecv);
return ncclSuccess;
}
static ncclResult_t openRing(struct ncclTree* tree, int rank, int upRank) {
if (tree->down[0] == upRank) tree->down[0] = -1;
if (rank == upRank) tree->up = -1;
return ncclSuccess;
}
Then execute openRing, transforming from Figure 3 to Figure 5. If current rank’s child node is sendrank, break this chain (like rank 7 in Figure 5). If current rank is sendrank, break the up link (like rank 0 in Figure 5).

Figure 5#
If current node is sendrank, execute setTreeUp to set sendrank’s parent node. channel0 is actually indexesRecv[u0], channel1 is indexesRecv[u1]. Similarly, use setTreeDown to set recvrank’s child nodes. After completion, we get Figure 2.
This completes ncclTopoPostset, then establish tree communication links. Current rank receives data from treeUp.down and sends data to treeUp.up. As mentioned before, since treeDn is identical to treeUp, connections for receiving data from treeUp.up and sending to treeUp.down are also established.
for (int c=0; c<comm->nChannels; c++) {
struct ncclChannel* channel = comm->channels+c;
...
NCCLCHECKGOTO(ncclTransportP2pSetup(comm, &treeGraph, channel, NCCL_MAX_TREE_ARITY, channel->treeUp.down, 1, &channel->treeUp.up), ret, affinity_restore);
NCCLCHECKGOTO(ncclTransportP2pSetup(comm, &treeGraph, channel, 1, &channel->treeDn.up, NCCL_MAX_TREE_ARITY, channel->treeDn.down), ret, affinity_restore);
}
enqueue#
The enqueue process is exactly the same as ring allreduce. Let’s look directly at computeColl in ncclSaveKernel.
static ncclResult_t computeColl(struct ncclInfo* info /* input */, struct ncclColl* coll, struct ncclProxyArgs* proxyArgs /* output */) {
coll->args.sendbuff = info->sendbuff;
coll->args.recvbuff = info->recvbuff;
coll->args.comm = info->comm->devComm;
...
// Set nstepsPerLoop and nchunksPerLoop
NCCLCHECK(getAlgoInfo(info));
NCCLCHECK(getPatternInfo(info));
NCCLCHECK(getLoopInfo(info));
...
}
First, use getAlgoInfo to select the protocol and algorithm. Assume the algorithm is NCCL_ALGO_TREE and the protocol is NCCL_PROTO_SIMPLE.
Then use getPatternInfo to select the pattern, which gives us ncclPatternTreeUpDown.
case ncclCollAllReduce:
info->pattern = info->algorithm == NCCL_ALGO_COLLNET ? ncclPatternCollTreeUp : info->algorithm == NCCL_ALGO_TREE ? ncclPatternTreeUpDown : ncclPatternRingTwice; break;
Then use getLoopInfo to calculate nstepsPerLoop and nchunksPerLoop. For tree, each loop only needs to reduce and send, so both are 1.
info->nstepsPerLoop = info-> nchunksPerLoop = 1;
stepSize is the size of one slot in the buffer. Both chunkSteps and sliceSteps are 1, so chunkSize is initialized as stepSize*chunkSteps, which is stepSize.
Then begin adjusting chunkSize based on tree height. When nsteps is relatively small, the entire tree cannot be pipelined. The three cases here are presumably corresponding to pipeline depths for scenarios with 8 cards, 4 cards, and single card per machine.
Then set proxy parameters. Since one loop can process data of chunkSize, and there are nChannels channels, the total amount of data that can be processed at once is (info->nChannels)info->nchunksPerLoopchunkEffectiveSize. Dividing nBytes by this gives us the total number of loops (nLoops). Then start calculating how many slots are needed (nsteps). With nLoops loops, each loop executes nstepsPerLoop chunks, and each chunk has chunkSteps steps, so nsteps equals nstepsPerLoop * nLoops * chunkSteps. However, for tree scenarios, nsteps equals nLoops.
static ncclResult_t computeColl(struct ncclInfo* info /* input */, struct ncclColl* coll, struct ncclProxyArgs* proxyArgs /* output */) {
...
coll->args.coll.root = info->root;
coll->args.coll.count = info->count;
coll->args.coll.nChannels = info->nChannels;
coll->args.coll.nThreads = info->nThreads;
coll->funcIndex = FUNC_INDEX(info->coll, info->op, info->datatype, info->algorithm, info->protocol);
int stepSize = info->comm->buffSizes[info->protocol]/NCCL_STEPS;
int chunkSteps = (info->protocol == NCCL_PROTO_SIMPLE && info->algorithm == NCCL_ALGO_RING) ? info->chunkSteps : 1;
int sliceSteps = (info->protocol == NCCL_PROTO_SIMPLE && info->algorithm == NCCL_ALGO_RING) ? info->sliceSteps : 1;
int chunkSize = stepSize*chunkSteps;
// Compute lastChunkSize
if (info->algorithm == NCCL_ALGO_TREE && info->protocol == NCCL_PROTO_SIMPLE) {
if (info->pattern == ncclPatternTreeUpDown) {
// Optimize chunkSize / nSteps
while (info->nBytes / (info->nChannels*chunkSize) < info->comm->channels[0].treeUp.depth*8 && chunkSize > 131072) chunkSize /= 2;
while (info->nBytes / (info->nChannels*chunkSize) < info->comm->channels[0].treeUp.depth*4 && chunkSize > 65536) chunkSize /= 2;
while (info->nBytes / (info->nChannels*chunkSize) < info->comm->channels[0].treeUp.depth && chunkSize > 32768) chunkSize /= 2;
}
// Use lastChunkSize as chunkSize
coll->args.coll.lastChunkSize = chunkSize / ncclTypeSize(info->datatype);
} else if (info->algorithm == NCCL_ALGO_COLLNET && info->protocol == NCCL_PROTO_SIMPLE) {
...
} else if (info->protocol == NCCL_PROTO_LL) {
...
} else if (info->algorithm == NCCL_ALGO_TREE && info->protocol == NCCL_PROTO_LL128) {
...
}
int chunkEffectiveSize = chunkSize;
...
int nLoops = (int)(DIVUP(info->nBytes, (((size_t)(info->nChannels))*info->nchunksPerLoop*chunkEffectiveSize)));
proxyArgs->nsteps = info->nstepsPerLoop * nLoops * chunkSteps;
proxyArgs->sliceSteps = sliceSteps;
proxyArgs->chunkSteps = chunkSteps;
proxyArgs->protocol = info->protocol;
proxyArgs->opCount = info->comm->opCount;
proxyArgs->dtype = info->datatype;
proxyArgs->redOp = info->op;
TRACE(NCCL_NET,"opCount %lx slicesteps %d spl %d cpl %d nbytes %zi -> protocol %d nchannels %d nthreads %d, nloops %d nsteps %d comm %p",
coll->args.opCount, proxyArgs->sliceSteps, info->nstepsPerLoop, info->nchunksPerLoop, info->nBytes, info->protocol, info->nChannels, info->nThreads,
nLoops, proxyArgs->nsteps, info->comm);
return ncclSuccess;
}
kernel execution#
The subsequent process is very similar to ring allreduce. Looking directly at kernel launch, the kernel here is ncclAllReduceTreeKernel.
Count is the user data length, loopSize is the amount of data all channels can process in one loop, thisInput and thisOutput are user-provided input and output.
template<int UNROLL, class FUNC, typename T>
__device__ void ncclAllReduceTreeKernel(struct CollectiveArgs* args) {
const int tid = threadIdx.x;
const int nthreads = args->coll.nThreads-WARP_SIZE;
const int bid = args->coll.bid;
const int nChannels = args->coll.nChannels;
struct ncclDevComm* comm = args->comm;
struct ncclChannel* channel = comm->channels+blockIdx.x;
const int stepSize = comm->buffSizes[NCCL_PROTO_SIMPLE] / (sizeof(T)*NCCL_STEPS);
int chunkSize = args->coll.lastChunkSize;
const ssize_t minChunkSize = nthreads*8*sizeof(uint64_t) / sizeof(T);
const ssize_t loopSize = nChannels*chunkSize;
const ssize_t size = args->coll.count;
...
const T * __restrict__ thisInput = (const T*)args->sendbuff;
T * __restrict__ thisOutput = (T*)args->recvbuff;
...
}
Then begin the reduce phase, which is the tree’s upward phase. Create prims, receive data from treeUp’s down and send to treeUp’s up. Then iterate through all data. If up is -1, indicating root node, execute recvReduceCopy to receive data from child nodes, reduce with own data, and copy to user output. If down[0] is -1, indicating leaf node, use send to copy data from user input to parent node’s buffer. For intermediate nodes, execute recvReduceSend to receive data from child nodes, reduce with own user input, then send to parent node.
do {
struct ncclTree* tree = &channel->treeUp;
// Reduce : max number of recv is 3, max number of send is 1 (binary tree + local)
ncclPrimitives<UNROLL/2, 1, 1, T, NCCL_MAX_TREE_ARITY, 1, 0, FUNC> prims(tid, nthreads, tree->down, &tree->up, NULL, stepSize, channel, comm);
for (ssize_t gridOffset = 0; gridOffset < size; gridOffset += loopSize) {
// Up
ssize_t offset = gridOffset + bid*chunkSize;
int nelem = min(chunkSize, size-offset);
if (tree->up == -1) {
prims.recvReduceCopy(thisInput+offset, thisOutput+offset, nelem);
} else if (tree->down[0] == -1) {
prims.send(thisInput+offset, nelem);
} else {
prims.recvReduceSend(thisInput+offset, nelem);
}
}
} while(0);
After execution completes, reduce is finished and the root node has the global reduce result. Then begin executing allgather. Create prim, and as mentioned above, treeDn is actually treeUp, so prim will receive data from treeUp’s up rank and send to treeUp’s down rank. If up is -1, indicating root node, use directSend to send data directly from user output to child node’s buffer. If down[0] is -1, indicating leaf node, use directRecv to copy data from parent node’s buffer to user output. If it’s an intermediate node, use directRecvCopySend to receive data from parent node’s buffer, copy to own user output, and send to child node’s buffer.
do {
struct ncclTree* tree = &channel->treeDn;
// Broadcast : max number of recv is 1, max number of send is 3 (binary tree + local)
ncclPrimitives<UNROLL/2, 1, 1, T, 1, NCCL_MAX_TREE_ARITY, 1, FUNC> prims(tid, nthreads, &tree->up, tree->down, thisOutput, stepSize, channel, comm);
for (ssize_t gridOffset = 0; gridOffset < size; gridOffset += loopSize) {
// Down
ssize_t offset = gridOffset + bid*chunkSize;
int nelem = min(chunkSize, size-offset);
if (tree->up == -1) {
prims.directSend(thisOutput+offset, offset, nelem);
} else if (tree->down[0] == -1) {
prims.directRecv(thisOutput+offset, offset, nelem);
} else {
prims.directRecvCopySend(thisOutput+offset, offset, nelem);
}
}
} while(0);
proxy#
Here we’ve seen the kernel execution process, now let’s look at the proxy flow. We can see it saves recv args to treeUp child nodes and send args to treeUp parent nodes. It also saves send args to treeDn child nodes and recv args to treeDn parent nodes.
ncclResult_t ncclProxySaveColl(struct ncclProxyArgs* args, int pattern, int root, int nranks) {
...
if (pattern == ncclPatternTreeUp || pattern == ncclPatternTreeUpDown) {
// Tree up
struct ncclTree* tree = &args->channel->treeUp;
for (int i=0; i<NCCL_MAX_TREE_ARITY; i++) NCCLCHECK(SaveProxy<proxyRecv>(tree->down[i], args));
NCCLCHECK(SaveProxy<proxySend>(tree->up, args));
}
if (pattern == ncclPatternTreeDown || pattern == ncclPatternTreeUpDown) {
// Tree down
struct ncclTree* tree = &args->channel->treeDn;
for (int i=0; i< NCCL_MAX_TREE_ARITY; i++) NCCLCHECK(SaveProxy<proxySend>(tree->down[i], args));
NCCLCHECK(SaveProxy<proxyRecv>(tree->up, args));
}
...
return ncclSuccess;
}
choosing between ring and tree#
The main idea is simple. For user-provided data length nBytes, total time = latency + nBytes / algo_bw, where algo_bw is algorithm bandwidth. Base bus bandwidth (busBw) is channel bandwidth times number of channels, then bandwidth is adjusted based on measured data - for example, tree scenarios multiply by 0.9. Then calculate algorithm bandwidth: tree divides by 2 because it sends data twice (up and down), ring divides by 2 * (nranks - 1) / nranks for reasons covered in section 11. Latency calculation won’t be repeated here. Finally, save calculated bandwidth and latency for each protocol and algorithm combination to bandwidths and latencies.
When users execute the allreduce API, getAlgoInfo calculates execution time for each algorithm and protocol combination to select the optimal one.
ncclResult_t ncclTopoTuneModel(struct ncclComm* comm, int minCompCap, int maxCompCap, struct ncclTopoGraph** graphs) {
int simpleDefaultThreads = (graphs[NCCL_ALGO_RING]->bwIntra*graphs[NCCL_ALGO_RING]->nChannels <= PCI_BW) ? 256 : NCCL_SIMPLE_MAX_NTHREADS;
...
for (int coll=0; coll<NCCL_NUM_FUNCTIONS; coll++) {
int nsteps = coll == ncclFuncAllReduce ? 2*(nRanks-1) :
coll == ncclFuncReduceScatter || coll == ncclFuncAllGather ? nRanks-1 :
nRanks;
int nInterSteps = coll == ncclFuncAllReduce ? (nNodes > 1 ? 2*nNodes :0) :
coll == ncclFuncReduceScatter || coll == ncclFuncAllGather ? nNodes-1 :
nNodes;
for (int a=0; a<NCCL_NUM_ALGORITHMS; a++) {
if (coll == ncclFuncBroadcast && a != NCCL_ALGO_RING) continue;
if (coll == ncclFuncReduce && a != NCCL_ALGO_RING) continue;
if (coll == ncclFuncReduceScatter && a != NCCL_ALGO_RING && a != NCCL_ALGO_NVLS) continue;
if (coll == ncclFuncAllGather && a != NCCL_ALGO_RING && a != NCCL_ALGO_NVLS) continue;
for (int p=0; p<NCCL_NUM_PROTOCOLS; p++) {
...
float busBw = graphs[a]->nChannels * bw;
// Various model refinements
if (a == NCCL_ALGO_RING && p == NCCL_PROTO_LL) { busBw = std::min(llMaxBw, busBw * ((nNodes > 1 || coll == ncclFuncAllReduce || coll == ncclFuncReduce) ? 1.0/4.0 : 1.0/3.0)); }
if (a == NCCL_ALGO_RING && p == NCCL_PROTO_LL128) busBw = std::min(busBw * (ppn < 2 ? 0.7 : 0.92 /*120.0/128.0*/), graphs[a]->nChannels*perChMaxRingLL128Bw);
if (a == NCCL_ALGO_TREE) busBw = std::min(busBw*.92, graphs[a]->nChannels*perChMaxTreeBw);
if (a == NCCL_ALGO_TREE && p == NCCL_PROTO_LL) busBw = std::min(busBw*1.0/3.8, llMaxBw);
if (a == NCCL_ALGO_TREE && p == NCCL_PROTO_LL128) busBw = std::min(busBw * (nNodes == 1 ? 7.0/9.0 : 120.0/128.0), graphs[a]->nChannels*perChMaxTreeLL128Bw);
if (a == NCCL_ALGO_TREE && graphs[a]->pattern == NCCL_TOPO_PATTERN_TREE) busBw *= .85;
...
// Convert bus BW to algorithm BW
float ratio;
if (a == NCCL_ALGO_RING) ratio = (1.0 * nRanks) / nsteps;
else if (a == NCCL_ALGO_NVLS || a == NCCL_ALGO_NVLS_TREE) ratio = 5.0/6.0;
else ratio = .5;
comm->bandwidths[coll][a][p] = busBw * ratio;
...
}
}
References#
Two-Tree Algorithms for Full Bandwidth Broadcast, Reduction and Scan