SVD

By Su Jianlin | 2024-10-01 | 29334 Readers

In the previous article, we introduced “pseudoinverse,” which relates to the optimal solution of the optimization objective $\Vert \boldsymbol{A}\boldsymbol{B} - \boldsymbol{M}\Vert_F^2$ when matrices $\boldsymbol{M}$ and $\boldsymbol{A}$ (or $\boldsymbol{B}$) are given. In this article, we will focus on the optimal solution when neither $\boldsymbol{A}$ nor $\boldsymbol{B}$ is given, i.e.,

where $\boldsymbol{A}\in\mathbb{R}^{n\times r}, \boldsymbol{B}\in\mathbb{R}^{r\times m}, \boldsymbol{M}\in\mathbb{R}^{n\times m}$, and $r < \min(n,m)$. In simple terms, this is about finding the “optimal $r$-rank approximation (the best approximation with rank not exceeding $r$)” of matrix $\boldsymbol{M}$. To solve this problem, we need to introduce the famous “SVD (Singular Value Decomposition).” Although this series begins with the pseudoinverse, its “fame” is far less than that of SVD. Many people have heard of or even used SVD but have never heard of the pseudoinverse, including the author, who learned about SVD before encountering the pseudoinverse.

Next, we will elaborate on SVD, focusing on the optimal low-rank approximation of matrices.

Initial Exploration of Conclusions

#

For any matrix $\boldsymbol{M}\in\mathbb{R}^{n\times m}$, a singular value decomposition (SVD) of the following form can be found:

where $\boldsymbol{U}\in\mathbb{R}^{n\times n}$ and $\boldsymbol{V}\in\mathbb{R}^{m\times m}$ are orthogonal matrices, and $\boldsymbol{\Sigma}\in\mathbb{R}^{n\times m}$ is a non-negative diagonal matrix:

The diagonal elements are by default sorted in descending order, i.e., $\sigma_1\geq \sigma_2\geq\sigma_3\geq\cdots\geq 0$. These diagonal elements are called singular values. From a numerical computation perspective, we can retain only the non-zero elements in $\boldsymbol{\Sigma}$, reducing the sizes of $\boldsymbol{U}, \boldsymbol{\Sigma}, \boldsymbol{V}$ to $n\times r, r\times r, m\times r$ respectively ($r$ is the rank of $\boldsymbol{M}$). Retaining complete orthogonal matrices is more convenient for theoretical analysis.

SVD also holds for complex matrices, but orthogonal matrices need to be replaced by unitary matrices, and transposes by conjugate transposes. However, here we primarily focus on real matrix results, which are more closely related to machine learning. The fundamental theory of SVD includes its existence, computation methods, and its connection with optimal low-rank approximation. The author will provide his own understanding of these topics later.

In a 2D plane, SVD has a very intuitive geometric meaning. 2D orthogonal matrices are mainly rotations (there are also reflections, but for geometric intuition, we can be less rigorous). Therefore, $\boldsymbol{M}\boldsymbol{x}=\boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}\boldsymbol{x}$ means that any linear transformation of a (column) vector $x$ can be decomposed into three steps: rotation, scaling, and rotation, as shown in the figure below:

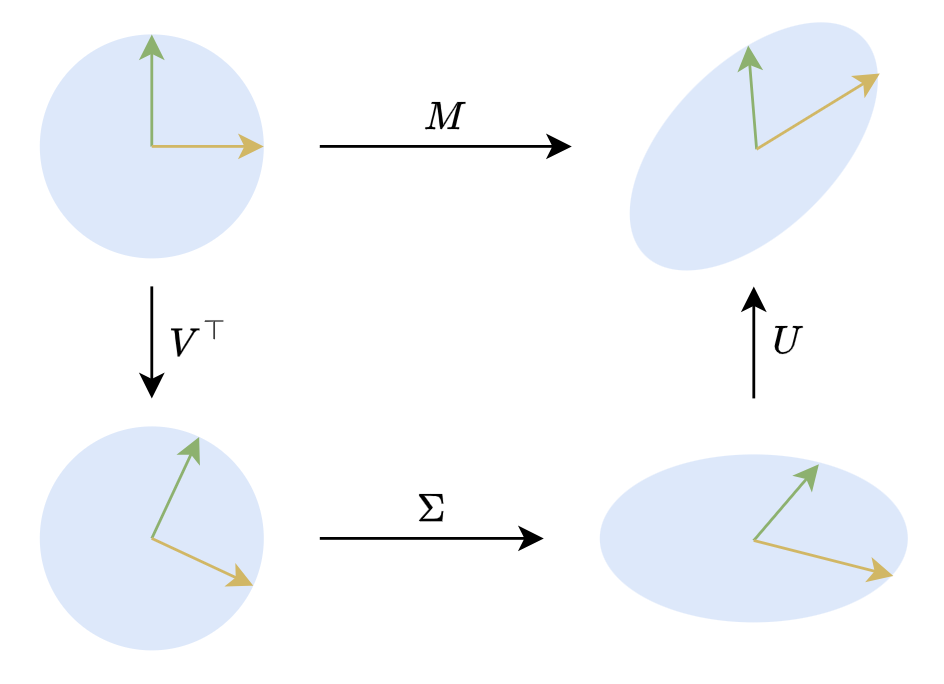
Geometric Meaning of SVD

Some Applications

#

SVD has very wide applications in both theoretical analysis and numerical computation. One of the underlying principles is that common matrix/vector norms are invariant under orthogonal transformations. Therefore, the characteristic of SVD having a diagonal matrix sandwiched between two orthogonal matrices often allows many matrix-related optimization objectives to be converted into equivalent special cases involving non-negative diagonal matrices, simplifying the problem.

General Solution for Pseudoinverse

#

Taking the pseudoinverse as an example, when $\boldsymbol{A}\in\mathbb{R}^{n\times r}$ has rank $r$, we have

In the previous article, we derived the expression for $\boldsymbol{A}^{\dagger}$ by differentiation, and then put some effort into generalizing it to cases where the rank of $\boldsymbol{A}$ is less than $r$. However, if SVD is introduced, the problem becomes much simpler. We can decompose $\boldsymbol{A}$ into $\boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}$, and then express $\boldsymbol{B}$ as $\boldsymbol{V} \boldsymbol{Z} \boldsymbol{U}^{\top}$. Note that we do not specify $\boldsymbol{Z}$ to be a diagonal matrix, so $\boldsymbol{B}=\boldsymbol{V} \boldsymbol{Z} \boldsymbol{U}^{\top}$ is always achievable. Thus,

The last equality is based on the conclusion we proved in the previous article, “orthogonal transformations do not change the Frobenius norm.” This way, we simplify the problem to finding the pseudoinverse of the diagonal matrix $\boldsymbol{\Sigma}$. Next, we can express $\boldsymbol{\Sigma} \boldsymbol{Z} - \boldsymbol{I}_n$ in block matrix form as

The slicing here should be understood according to Python array rules. From the final form, it can be seen that to minimize the Frobenius norm of $\boldsymbol{\Sigma} \boldsymbol{Z} - \boldsymbol{I}_n$, the unique solution is $\boldsymbol{Z}_{[:r,:r]}=\boldsymbol{\Sigma}_{[:r,:r]}^{-1}$ and $\boldsymbol{Z}_{[:r,r:]}=\boldsymbol{0}_{r\times(n-r)}$. In essence, $\boldsymbol{Z}$ is obtained by taking the reciprocal of all non-zero elements of $\boldsymbol{\Sigma}^{\top}$ and then transposing it. We denote this as $\boldsymbol{\Sigma}^{\dagger}$, so under SVD, we have

It can be further proven that this result also applies to $\boldsymbol{A}$ with rank less than $r$, making it a general form that some tutorials directly use as the definition of the pseudoinverse. Furthermore, we can observe that this form does not distinguish between left and right pseudoinverses, indicating that the left and right pseudoinverses of the same matrix are equal. Therefore, there is no need to specifically differentiate between left and right when referring to the pseudoinverse.

Matrix Norms

#

Using the conclusion that orthogonal transformations do not change the Frobenius norm, we can also derive

That is, the sum of the squares of the singular values equals the square of the Frobenius norm. Besides the Frobenius norm, SVD can also be used to calculate the “spectral norm.” In the previous article, we mentioned that the Frobenius norm is just one type of matrix norm. Another commonly used matrix norm is the spectral norm, which is induced from vector norms and defined as:

Note that the norms appearing on the right-hand side of the equality are vector norms (magnitude, 2-norm), so the above definition is well-defined. Numerically, the spectral norm of a matrix equals its largest singular value, i.e., $\Vert \boldsymbol{M}\Vert_2 = \sigma_1$. To prove this, one only needs to perform SVD on $\boldsymbol{M}$ as $\boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}$, and then substitute it into the definition of the spectral norm

The second equality precisely utilizes the property that orthogonal matrices do not change vector norms. Now we have simplified the problem to finding the spectral norm of the diagonal matrix $\boldsymbol{\Sigma}$, which is relatively simple. Let $\boldsymbol{y} = (y_1,y_2,\cdots,y_m)$, then

Therefore, $\Vert \boldsymbol{\Sigma} \boldsymbol{y}\Vert$ does not exceed $\sigma_1$, and the equality holds when $\boldsymbol{y}=(1,0,\cdots,0)$, so $\Vert \boldsymbol{M}\Vert_2=\sigma_1$. Comparing with the Frobenius norm result, we can also find that $\Vert \boldsymbol{M}\Vert_2\leq \Vert \boldsymbol{M}\Vert_F$ always holds.

Low-Rank Approximation

#

Finally, let’s return to the main topic of this article: optimal low-rank approximation, which is the objective $\mathop{\text{argmin}}_{\boldsymbol{A},\boldsymbol{B}}\Vert \boldsymbol{A}\boldsymbol{B} - \boldsymbol{M}\Vert_F^2$ introduced at the beginning. Decomposing $\boldsymbol{M}$ into $\boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}$, we can then write

Note that $\boldsymbol{U}^{\top}\boldsymbol{A}\boldsymbol{B}\boldsymbol{V}$ can still represent any matrix with rank not exceeding $r$. Therefore, by using SVD, we simplify the problem of finding the optimal $r$-rank approximation of matrix $\boldsymbol{M}$ to finding the optimal $r$-rank approximation of the non-negative diagonal matrix $\boldsymbol{\Sigma}$.

In “Aligning Full Fine-Tuning! This is the Most Brilliant LoRA Improvement I’ve Seen (I)”, we used a similar approach to solve an analogous optimization problem:

Utilizing SVD and the property that orthogonal transformations do not change the Frobenius norm, we can obtain

This transforms the original optimization problem for a general matrix $\boldsymbol{M}$ into a special case where $\boldsymbol{M}$ is a non-negative diagonal matrix, reducing the difficulty of analysis. Note that if the ranks of $\boldsymbol{A}$ and $\boldsymbol{B}$ do not exceed $r$, then the rank of $\boldsymbol{A}\boldsymbol{A}^{\top}\boldsymbol{M} + \boldsymbol{M}\boldsymbol{B}^{\top}\boldsymbol{B}$ is at most $2r$ (assuming $2r < \min(n,m)$). Therefore, the original problem is also about finding the optimal $2r$-rank approximation of $\boldsymbol{M}$. After transformation into a non-negative diagonal matrix, it becomes finding the optimal $2r$-rank approximation of a non-negative diagonal matrix, which is essentially the same as the previous problem.

Theoretical Basis

#

After affirming the role of SVD, we need to supplement with some theoretical proofs. First, we need to ensure the existence of SVD, and second, we need to find at least one computation method. Only then can various applications of SVD be considered truly feasible. Next, we will address both of these issues using a single process.

Spectral Theorem

#

Spectral Theorem For any real symmetric matrix $\boldsymbol{M}\in\mathbb{R}^{n\times n}$, there exists a spectral decomposition (also known as eigenvalue decomposition)

where $\boldsymbol{U},\boldsymbol{\Lambda}\in\mathbb{R}^{n\times n}$, $\boldsymbol{U}$ is an orthogonal matrix, and $\boldsymbol{\Lambda}=\text{diag}(\lambda_1,\cdots,\lambda_n)$ is a diagonal matrix.

In essence, the spectral theorem asserts that any real symmetric matrix can be diagonalized by an orthogonal matrix, based on the following two properties:

1. The eigenvalues and eigenvectors of a real symmetric matrix are real;
2. Eigenvectors corresponding to distinct eigenvalues of a real symmetric matrix are orthogonal.

The proof of these two properties is actually quite simple, so it will not be elaborated on here. Based on these two points, we can immediately conclude that if a real symmetric matrix $\boldsymbol{M}$ has $n$ distinct eigenvalues, then the spectral theorem holds:

where $\lambda_1,\lambda_2,\cdots,\lambda_n$ are the eigenvalues, and $\boldsymbol{u}_1,\boldsymbol{u}_2,\cdots,\boldsymbol{u}_n$ are the corresponding unit eigen (column) vectors. Written in matrix multiplication form, it is $\boldsymbol{M}\boldsymbol{U}=\boldsymbol{U}\boldsymbol{\Lambda}$, so $\boldsymbol{M} = \boldsymbol{U}\boldsymbol{\Lambda} \boldsymbol{U}^{\top}$. The difficulty of the proof lies in how to extend it to cases with equal eigenvalues. However, before considering a complete proof, we can first gain an informal intuition that this result for distinct eigenvalues can certainly be generalized to the general case.

Why say this? From a numerical perspective, the probability of two real numbers being absolutely equal is almost zero, so there’s no need to consider cases where eigenvalues are equal; in more mathematical terms, real matrices with distinct eigenvalues are dense in the set of all real matrices. Thus, we can always find a family of matrices $\boldsymbol{M}_{\epsilon}$ such that for $\epsilon > 0$, its eigenvalues are all distinct, and as $\epsilon \to 0$, it equals $\boldsymbol{M}$. This way, each $\boldsymbol{M}_{\epsilon}$ can be decomposed into $\boldsymbol{U}_{\epsilon}\boldsymbol{\Lambda} _{\epsilon}\boldsymbol{U}_{\epsilon}^{\top}$, and taking the limit as $\epsilon\to 0$ yields the spectral decomposition of $\boldsymbol{M}$.

Mathematical Induction

#

Unfortunately, the above paragraph can only serve as an intuitive but informal understanding, because transforming it into a rigorous proof is still very difficult. In fact, perhaps the simplest way to rigorously prove the spectral theorem is by mathematical induction, i.e., assuming that any $(n-1)$-order real symmetric square matrix can be spectrally decomposed, we prove that $\boldsymbol{M}$ can also be spectrally decomposed.

The key idea of the proof is to decompose $\boldsymbol{M}$ into a certain eigenvector and its $(n-1)$-dimensional orthogonal subspace, thereby allowing the inductive hypothesis to be applied. Specifically, let $\lambda_1$ be a non-zero eigenvalue of $\boldsymbol{M}$, and $\boldsymbol{u}_1$ be the corresponding unit eigenvector. Then we have $\boldsymbol{M}\boldsymbol{u}_1 = \lambda_1 \boldsymbol{u}_1$. We can supplement with $n-1$ unit vectors $\boldsymbol{Q}=(\boldsymbol{q}_2,\cdots,\boldsymbol{q}_n)$ that are orthogonal to $\boldsymbol{u}_1$, such that $(\boldsymbol{u}_1,\boldsymbol{q}_2,\cdots,\boldsymbol{q}_n)=(\boldsymbol{u}_1,\boldsymbol{Q})$ becomes an orthogonal matrix. Now we consider

Note that $\boldsymbol{Q}^{\top} \boldsymbol{M} \boldsymbol{Q}$ is an $(n-1)$-order square matrix, and it is clearly a real symmetric matrix. Therefore, by assumption, it can be spectrally decomposed as $\boldsymbol{V} \boldsymbol{\Lambda}_2 \boldsymbol{V}^{\top}$, where $\boldsymbol{V}$ is an $(n-1)$-order orthogonal matrix, and $\boldsymbol{\Lambda}_2$ is an $(n-1)$-order diagonal matrix. Then we have $(\boldsymbol{Q}\boldsymbol{V})^{\top} \boldsymbol{M} \boldsymbol{Q}\boldsymbol{V}= \boldsymbol{\Lambda}_2$. Based on this result, we consider $\boldsymbol{U} = (\boldsymbol{u}_1, \boldsymbol{Q}\boldsymbol{V})$. It can be verified that it is also an orthogonal matrix, and

That is to say, $\boldsymbol{U}$ is precisely the orthogonal matrix that can diagonalize $\boldsymbol{M}$. Therefore, $\boldsymbol{M}$ can undergo spectral decomposition, completing the most crucial step of mathematical induction.

Singular Decomposition

#

At this point, all preparations are complete. We can now formally prove the existence of SVD and provide a practical computation scheme.

In the previous section, we introduced spectral decomposition. It is not difficult to see its similarity with SVD, but there are also two distinct differences: 1. Spectral decomposition applies only to real symmetric matrices, while SVD applies to any real matrix; 2. The diagonal matrix $\boldsymbol{\Sigma}$ in SVD is non-negative, whereas $\boldsymbol{\Lambda}$ in spectral decomposition is not necessarily so. So, what is their specific connection? It is easy to verify that if the SVD of $\boldsymbol{M}$ is $\boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}$, then

Note that both $\boldsymbol{\Sigma}\boldsymbol{\Sigma}^{\top}$ and $\boldsymbol{\Sigma}^{\top}\boldsymbol{\Sigma}$ are diagonal matrices. This implies that the spectral decompositions of $\boldsymbol{M}\boldsymbol{M}^{\top}$ and $\boldsymbol{M}^{\top}\boldsymbol{M}$ are $\boldsymbol{U}\boldsymbol{\Sigma}^2 \boldsymbol{U}^{\top}$ and $\boldsymbol{V}\boldsymbol{\Sigma}^2 \boldsymbol{V}^{\top}$, respectively. Does this mean that by performing spectral decomposition on $\boldsymbol{M}\boldsymbol{M}^{\top}$ and $\boldsymbol{M}^{\top}\boldsymbol{M}$ separately, we can obtain the SVD of $\boldsymbol{M}$? Indeed, this is a way to compute SVD, but we cannot directly prove that the resulting $\boldsymbol{U},\boldsymbol{\Sigma},\boldsymbol{V}$ satisfy $\boldsymbol{M}=\boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}$.

The key to solving the problem is to perform spectral decomposition on only one of $\boldsymbol{M}\boldsymbol{M}^{\top}$ or $\boldsymbol{M}^{\top}\boldsymbol{M}$, and then construct the orthogonal matrix on the other side using another method. Without loss of generality, let the rank of $\boldsymbol{M}$ be $r \leq m$. Consider performing spectral decomposition on $\boldsymbol{M}^{\top}\boldsymbol{M}$ as $\boldsymbol{V}\boldsymbol{\Lambda} \boldsymbol{V}^{\top}$. Note that $\boldsymbol{M}^{\top}\boldsymbol{M}$ is a positive semi-definite matrix, so $\boldsymbol{\Lambda}$ is non-negative. Assuming the diagonal elements are already sorted in descending order, a rank of $r$ means that only the first $r$ $\lambda_i$’s are greater than 0. We define

It can be verified that

Here, it is assumed that slicing has higher precedence than matrix operations like transpose and inverse, i.e., $\boldsymbol{U}_{[:n,:r]}^{\top}=(\boldsymbol{U}_{[:n,:r]})^{\top}$, $\boldsymbol{\Sigma}_{[:r,:r]}^{-1}=(\boldsymbol{\Sigma}_{[:r,:r]})^{-1}$, etc. The above result shows that $\boldsymbol{U}_{[:n,:r]}$ is part of an orthogonal matrix. Next, we have

Note that $\boldsymbol{M}\boldsymbol{V}\boldsymbol{V}^{\top} = \boldsymbol{M}$ always holds. $\boldsymbol{V}_{[:m,:r]}$ consists of the first $r$ columns of $\boldsymbol{V}$. According to $\boldsymbol{M}^{\top}\boldsymbol{M}=\boldsymbol{V}\boldsymbol{\Lambda} \boldsymbol{V}^{\top}$, we can write $(\boldsymbol{M}\boldsymbol{V})^{\top}\boldsymbol{M}\boldsymbol{V} = \boldsymbol{\Lambda}$. Let $\boldsymbol{V}=(\boldsymbol{v}_1,\boldsymbol{v}_2,\cdots,\boldsymbol{v}_m)$, then $\Vert \boldsymbol{M}\boldsymbol{v}_i\Vert^2=\lambda_i$. Due to the rank $r$ setting, $\lambda_i=0$ when $i > r$, which means $\boldsymbol{M}\boldsymbol{v}_i$ is actually a zero vector at that time. Therefore,

This shows that $\boldsymbol{U}_{[:n,:r]}\boldsymbol{\Sigma}_{[:r,:r]}\boldsymbol{V}_{[:m,:r]}^{\top}=\boldsymbol{M}$. Combined with the fact that $\boldsymbol{U}_{[:n,:r]}$ is part of an orthogonal matrix, we have obtained the crucial part of $\boldsymbol{M}$’s SVD. We only need to pad $\boldsymbol{\Sigma}_{[:r,:r]}$ with zeros to form an $n\times m$ matrix $\boldsymbol{\Sigma}$, and complete $\boldsymbol{U}_{[:n,:r]}$ to an $n\times n$ orthogonal matrix $\boldsymbol{U}$, thus obtaining the complete SVD form $\boldsymbol{M}=\boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}$.

Approximation Theorem

#

Finally, let’s not forget that our ultimate goal is the optimization problem $\mathop{\text{argmin}}_{\boldsymbol{A},\boldsymbol{B}}\Vert \boldsymbol{A}\boldsymbol{B} - \boldsymbol{M}\Vert_F^2$ from the beginning. With SVD, we can now provide the answer:

If the SVD of $\boldsymbol{M}\in\mathbb{R}^{n\times m}$ is $\boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}$, then the optimal $r$-rank approximation of $\boldsymbol{M}$ is $\boldsymbol{U}_{[:n,:r]}\boldsymbol{\Sigma}_{[:r,:r]} \boldsymbol{V}_{[:m,:r]}^{\top}$.

This is known as the “Eckart-Young-Mirsky Theorem”. In the section on SVD applications, titled “Low-Rank Approximation”, we showed that by using SVD, the problem of optimal $r$-rank approximation for a general matrix can be simplified to that of a non-negative diagonal matrix. Therefore, the “Eckart-Young-Mirsky Theorem” essentially states that the optimal $r$-rank approximation of a non-negative diagonal matrix is the matrix obtained by retaining only the $r$ largest diagonal elements.

Some readers might think, “Isn’t this obvious?” However, the truth is that while the conclusion is very intuitive, it is not trivial. Next, we will focus on solving:

where $\boldsymbol{A}\in\mathbb{R}^{n\times r}, \boldsymbol{B}\in\mathbb{R}^{r\times m}, \boldsymbol{\Sigma}\in\mathbb{R}^{n\times m}$, and $r < \min(n,m)$. If $\boldsymbol{A}$ is given, we have already found the optimal solution for $\boldsymbol{B}$ in the previous article, which is $\boldsymbol{A}^{\dagger} \boldsymbol{\Sigma}$. Therefore, we have

From the pseudoinverse calculation formula, $\boldsymbol{\Sigma}_{\boldsymbol{A}} \boldsymbol{\Sigma}_{\boldsymbol{A}}^{\dagger}$ is a diagonal matrix, where the first $r_{\boldsymbol{A}}$ elements on the diagonal are 1 ($r_{\boldsymbol{A}}\leq r$ is the rank of $\boldsymbol{A}$), and the rest are 0. Therefore, $(\boldsymbol{\Sigma}_{\boldsymbol{A}} \boldsymbol{\Sigma}_{\boldsymbol{A}}^{\dagger} - \boldsymbol{I}_n)\boldsymbol{U}_{\boldsymbol{A}}^{\top}$ is equivalent to retaining only the last $k=n-r_{\boldsymbol{A}}$ rows of the orthogonal matrix $\boldsymbol{U}_{\boldsymbol{A}}^{\top}$. Thus, it can ultimately be simplified to

Now, according to the definition of the Frobenius norm, we can write

Note that $0 \leq w_j \leq 1$, and $w_1+w_2+\cdots+w_n = k$. Under these constraints, the minimum value of the rightmost expression can only be the sum of the $k$ smallest $\sigma_j^2$. Since $\sigma_j$ are already sorted in descending order, we have

That is, the error (squared Frobenius norm) between $\boldsymbol{\Sigma}$ and its optimal $r$-rank approximation is $\sum\limits_{j=r+1}^n \sigma_j^2$, which is precisely the error generated by retaining only the $r$ largest diagonal elements. Therefore, we have proven that “the optimal $r$-rank approximation of a non-negative diagonal matrix is the matrix obtained by retaining only the $r$ largest diagonal elements.” Of course, this can only be considered one solution; we have not ruled out the possibility of multiple solutions.

It is worth noting that the Eckart-Young-Mirsky Theorem holds not only for the Frobenius norm but also for the spectral norm. The proof for the spectral norm is actually simpler and will not be elaborated on here. Interested readers can refer to the Wikipedia entry “Low-rank approximation” on their own.

Summary (formatted)

#

The main subject of this article is the well-known SVD (Singular Value Decomposition), which many readers are likely already familiar with. In this article, we mainly elaborated on the relationship between SVD and low-rank approximation, providing the simplest possible proof processes for theoretical aspects such as SVD’s existence, computation, and its connection to low-rank approximation.

@online{kexuefm-10407,
        title={The Path of Low-Rank Approximation (II): SVD},
        author={苏剑林},
        year={2024},
        month={10},
        url={\url{https://kexue.fm/archives/10407}},
}