Adding a Linear Transformation to the Codebook

In “VQ’s Rotation Trick: A Generalization of Straight-Through Estimator”, we introduced the Rotation Trick for VQ (Vector Quantization). Its core idea is to design better gradients for VQ by generalizing VQ’s STE (Straight-Through Estimator), thereby alleviating issues such as codebook collapse and low codebook utilization in VQ.

Coincidentally, a paper released yesterday on arXiv, “Addressing Representation Collapse in Vector Quantized Models with One Linear Layer”, proposed another trick to improve VQ: adding a linear transformation to the codebook. This trick simply changes the parameterization of the codebook without altering VQ’s underlying theoretical framework, yet it achieves excellent practical results, qualifying it as a classic example of simplicity and effectiveness.

Basics

#

Since we have introduced VQ and VQ-VAE multiple times in articles such as “A Concise Introduction to VQ-VAE: Quantized Autoencoders” and “Embarrassingly Simple FSQ: ‘Rounding’ Outperforms VQ-VAE”, we will not elaborate further here but directly present the mathematical forms of a standard AE and VQ-VAE:

Let me re-emphasize a common point: VQ-VAE is not a VAE; it is merely an AE augmented with VQ, lacking the generative capabilities of a VAE. VQ, on the other hand, is the operation of mapping any vector to the nearest vector in the codebook. This operation is inherently non-differentiable, so STE is used to design gradients for the encoder. Additionally, two new loss terms, $\beta$ and $\gamma$, are introduced to provide gradients for the codebook and regularize the encoder’s representations.

Changes

#

The paper refers to its proposed method as SimVQ, without explaining what Sim stands for. I speculate that Sim is short for Simple, as the changes introduced by SimVQ are indeed very simple:

That’s right, it’s just multiplying the codebook by an additional matrix $W$, with everything else left unchanged.

If VQ was originally trained using equation (1), then SimVQ can be directly and easily applied. If the codebook was updated using EMA (i.e., $\beta=0$, and a separate moving average process was used to update the codebook, which is the approach in VQ-VAE-2 and some subsequent models, mathematically equivalent to optimizing the codebook loss with SGD while other losses can use non-SGD optimizers like Adam), then this operation needs to be cancelled, and the $\beta$ term reintroduced for end-to-end optimization.

Some readers might immediately question: isn’t this just changing the parameterization of the codebook from $E$ to $EW$? $EW$ can be merged into a single matrix, equivalent to a new $E$, which theoretically shouldn’t change the model’s capacity? Yes, SimVQ does not change the model’s capacity, but it does change the learning process for optimizers like SGD and Adam, thereby affecting the quality of the learning outcome.

Experiments

#

Before further thought and analysis, let’s look at the experimental results of SimVQ. SimVQ conducted experiments on both vision and audio, with Table 1 being quite representative:

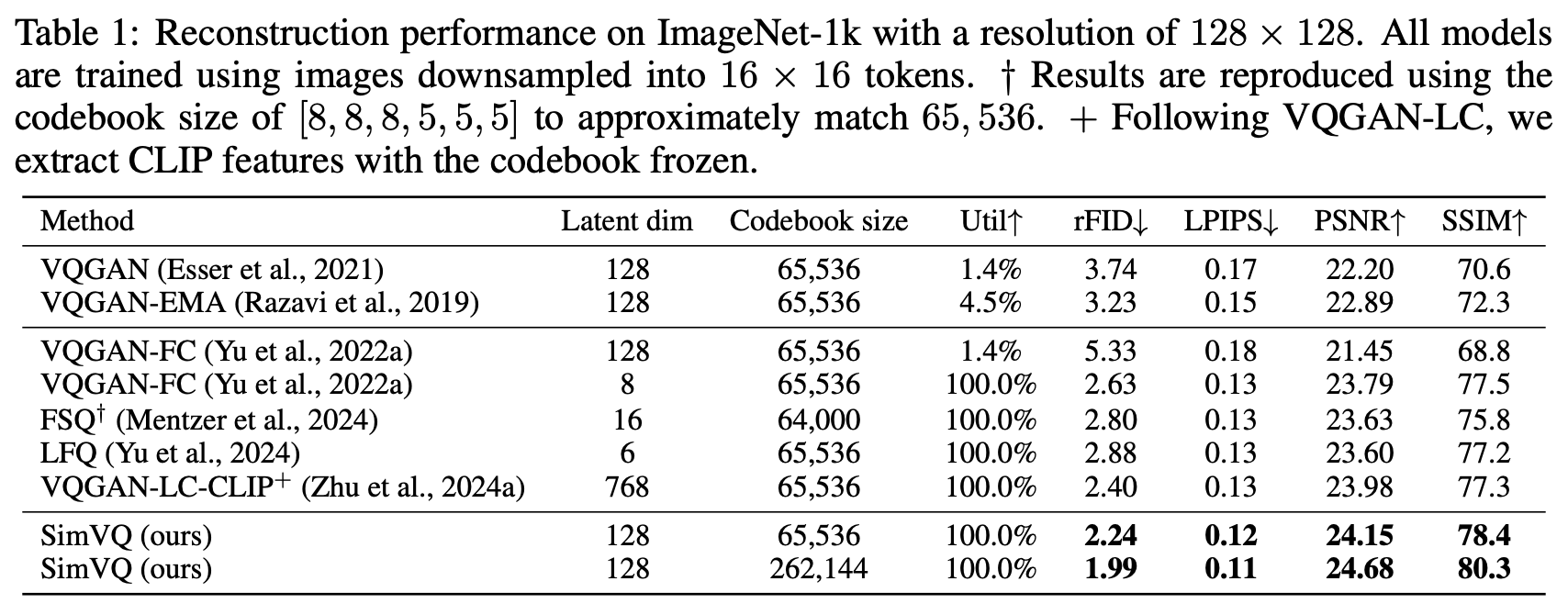
According to the paper’s description, the SimVQ code was modified from the first line of VQGAN’s code. The only change was inserting a linear transformation into the VQ layer, which resulted in significant improvements. It not only achieved optimal reconstruction quality with the same codebook size but also allowed for further improvements in reconstruction quality by increasing the codebook size, fully demonstrating SimVQ’s appeal — simple yet effective.

I also experimented with my previously written VQ-VAE code. Practical tests showed that the addition of this linear transformation significantly accelerated VQ-VAE’s convergence speed, and the final reconstruction loss was also reduced. I also experimented with a variant where $W$ is a diagonal matrix, which is equivalent to each code vector being element-wise multiplied by a parameter vector (initialized to all ones). The results showed that this variant also achieved similar effects, falling between VQ and SimVQ.

Analysis

#

Intuitively, VQ’s updates to the codebook are relatively “isolated.” For example, if a sample $z$ is quantized to $q$ by VQ, then the gradient for this sample will only affect $q$, not other vectors in the codebook. SimVQ is different: it not only updates $q$ but also updates $W$. From a geometric perspective, $W$ acts as the basis of the codebook. Once $W$ is updated, the entire codebook is updated. Therefore, SimVQ creates a more intimate “linkage” across the entire codebook, increasing the chances of finding better solutions instead of getting stuck in “fragmented” local optima.

Why can SimVQ improve codebook utilization? This is also not difficult to understand. Again, based on the explanation that $W$ is the basis of the codebook, if the codebook utilization is too low, $W$ will exhibit “anisotropy,” meaning the basis vectors will favor codes that are actually used. However, once the basis changes in this way, its linear combinations should also favor the utilized codes, preventing utilization from becoming too low. In essence, a learnable basis automatically increases its own utilization, thereby boosting the utilization of the entire codebook.

We can also describe this process from a mathematical formula perspective. Assuming the optimizer is SGD, the update for code $e_i$ in VQ is

Thus, if $e_i$ is not selected in the current batch, $\frac{\partial \mathcal{L}}{\partial e_i^{(t)}}$ will be zero, and the current codebook will not be updated. However, if $e_i$ is parameterized as $q_i W$, then

It can be seen that:

1. $W$ is updated based on the sum of gradients of all selected codes, so it naturally tends towards directions of high utilization;
2. Due to the presence of $q_i^{(t)}\sum_i q_i^{(t)}{}^{\top}\frac{\partial \mathcal{L}}{\partial e_i^{(t)}}$, the update for code $i$ will almost never be zero, regardless of whether it was selected or not;
3. $q_i^{(t)}\sum_i q_i^{(t)}{}^{\top}\frac{\partial \mathcal{L}}{\partial e_i^{(t)}}$ is essentially a projection onto the high-utilization direction, causing each code to move towards this direction.

However, extremes meet, and if all codes strongly move towards the direction of high utilization, it might instead lead to codebook collapse. Therefore, SimVQ defaults to a very conservative strategy: only $W$ is updated, and all $q$’s are not updated after random initialization. This virtually eliminates the possibility of codebook collapse. The good news is that, under appropriate code dimensions, experiments show that updating both $q$ and $W$ and only updating $W$ yield similar performance, so readers can choose the specific form according to their preference.

Extension

#

Setting aside the VQ context, approaches like SimVQ that introduce additional parameters, yet are mathematically equivalent (i.e., do not change the model’s theoretical fitting capacity, but only alter the dynamics of the optimization process), are known as “overparameterization.”

Overparameterization is not uncommon in neural networks. For instance, the mainstream architecture of current models is Pre Norm, i.e., $x + f(\text{RMSNorm}(x))$. The $\gamma$ vector multiplied at the end of RMSNorm is usually overparameterized because the first layer of $f$ is typically a linear transformation (e.g., Attention projects to Q, K, V via linear transformations, FFN uses linear transformations for up-dimensioning, etc.). In the inference phase, this $\gamma$ vector could be entirely merged into $f$’s linear transformation, yet it’s rare to see it removed during the training phase.

This is because many believe that overparameterization plays a crucial role in why deep learning models are “easy to train.” Therefore, rashly removing overparameterization from thoroughly validated models carries significant risk. Here, “easy to train” primarily refers to the incredible fact that gradient descent, a method theoretically prone to local optima, often finds solutions with excellent practical performance. Works such as “On the Optimization of Deep Networks: Implicit Acceleration by Overparameterization” also indicate that overparameterization implicitly accelerates training, similar to the role of momentum in SGD.

Finally, VQ can essentially be understood as a sparse training scheme. Thus, the insights and modifications brought by SimVQ might also be applicable to other sparse training models, such as MoE (Mixture of Experts). In current MoE training schemes, the updates between Experts are relatively independent, with only Experts selected by the Router updating their parameters. Is it possible, similar to SimVQ, to append a shared-parameter linear transformation after all Experts to improve Expert utilization efficiency? Of course, MoE itself has many differences from VQ, and this is merely a conjecture.

Summary (formatted)

#

This article introduced another training trick for VQ (Vector Quantization) — SimVQ — which involves simply adding a linear transformation to VQ’s codebook. Without any other changes, it achieves effects such as accelerated convergence, improved code utilization, and reduced reconstruction loss, making it remarkably simple and effective.

@online{kexuefm-10519,
        title={Another Trick for VQ: Adding a Linear Transformation to the Codebook},
        author={苏剑林},
        year={2024},
        month={11},
        url={\url{https://kexue.fm/archives/10519}},
}