How Adam's Epsilon Affects the Learning Rate Scaling Law?

In the previous article “How Should the Learning Rate Change When Batch Size Increases?”, we discussed the scaling law between learning rate and Batch Size from multiple perspectives. For the Adam optimizer, we adopted the SignSGD approximation, which is a common method for analyzing the Adam optimizer. A natural question then arises: how scientific is it to approximate Adam with SignSGD?

We know that the update amount denominator in the Adam optimizer includes an $\epsilon$, whose original purpose is to prevent division-by-zero errors. Therefore, its value is usually very close to zero, so much so that we often choose to ignore it during theoretical analysis. However, in current LLM training, especially low-precision training, we often choose a relatively large $\epsilon$. This leads to $\epsilon$ often exceeding the magnitude of squared gradients in the mid-to-late stages of training, making the presence of $\epsilon$ factually non-negligible.

Therefore, in this article, we attempt to explore how $\epsilon$ affects Adam’s learning rate and Batch Size scaling law, providing a reference computational scheme for related problems.

SoftSign

#

Since this article follows the previous one, I will not repeat the relevant background. To investigate the role of $\epsilon$, we switch from SignSGD to SoftSignSGD, i.e., $\tilde{\boldsymbol{u}}_B = \text{sign}(\tilde{\boldsymbol{g}}_B)$ becomes $\tilde{\boldsymbol{u}}_B = \text{softsign}(\tilde{\boldsymbol{g}}_B)$, where

This form is undoubtedly closer to Adam. But before that, we need to confirm whether $\epsilon$ is truly non-negligible to determine if further research is warranted.

In Keras’s Adam implementation, the default value for $\epsilon$ is $10^{-7}$, and in PyTorch, it’s $10^{-8}$. At these values, the probability of the absolute gradient value being less than $\epsilon$ is not very high; however, in LLMs, the common value for $\epsilon$ is $10^{-5}$ (e.g., LLAMA2). Once training gets “on track,” components where the absolute gradient value is less than $\epsilon$ will become very common, so the influence of $\epsilon$ is significant.

This also has some relation to the number of parameters in LLMs. For a model that can be trained stably, regardless of its parameter count, the magnitude of its gradients is roughly on the same order of magnitude. This is determined by the stability of backpropagation (refer to “What Difficulties Arise When Training a 1000-Layer Transformer?”). Consequently, for models with a larger number of parameters, the average absolute gradient value per parameter becomes relatively smaller, thus highlighting the role of $\epsilon$.

It is worth noting that the introduction of $\epsilon$ effectively provides an interpolation between Adam and SGD. This is because when $x\neq 0$,

Therefore, the larger $\epsilon$ is, the closer Adam’s behavior gets to SGD.

(Note: The concept of SoftSign in this article originated from an ongoing collaboration between the author, Dr. Liyuan Liu from MSR, and Mr. Chengyu Dong. We have decided to share this part of the results first after mutual discussion. Please stay tuned for more subsequent conclusions.)

S-shaped Approximation

#

Having confirmed the necessity of introducing $\epsilon$, we proceed with the analysis. During the analysis, we will repeatedly encounter S-shaped functions, so another preparatory task is to explore simple approximations for S-shaped functions.

S-shaped functions are likely familiar to everyone by now. The $\text{softsign}$ function introduced in the previous section is one such example, and the $\text{erf}$ function from the analysis in the last article is another; additionally, there are $\tanh$, $\text{sigmoid}$, etc. Next, we deal with S-shaped functions $S(x)$ that satisfy the following properties:

• 1. Globally smooth and monotonically increasing;
• 2. An odd function with a range of $[-1,1]$;
• 3. A slope of $k > 0$ at the origin.

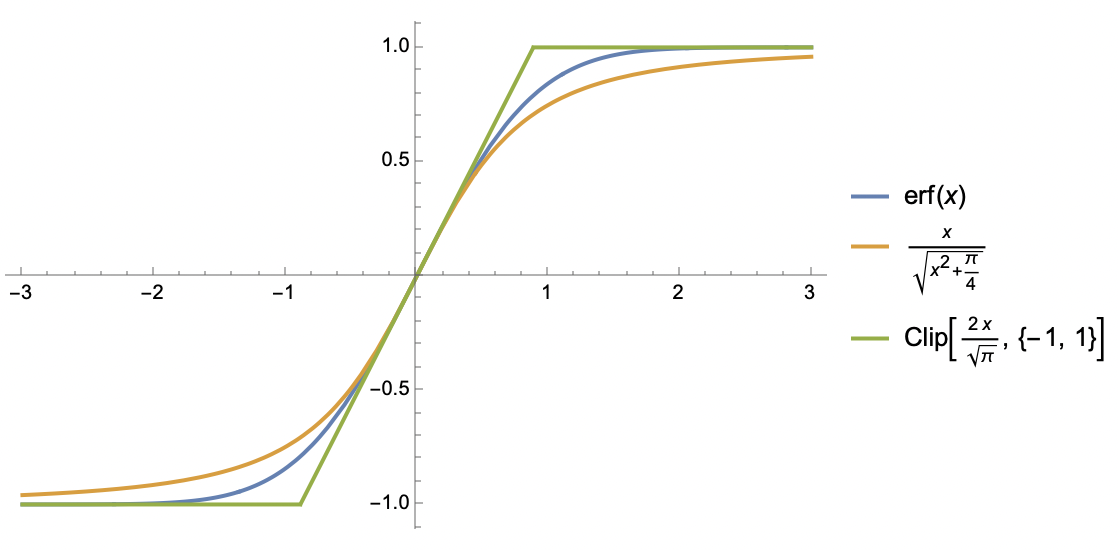
For such functions, we consider two approximations. The first approximation is similar to $\text{softsign}$:

This is arguably the simplest function that preserves the three properties of $S(x)$ mentioned above; the second approximation is based on the $\text{clip}$ function:

This is essentially a piecewise linear function, which sacrifices global smoothness, but piecewise linearity makes integrals easier to compute, as we will soon see.

Mean Estimation

#

Without further ado, following the method from the previous article, the starting point is still

What we need to do is estimate $\mathbb{E}[\tilde{\boldsymbol{u}}_B]$ and $\mathbb{E}[\tilde{\boldsymbol{u}}_B\tilde{\boldsymbol{u}}_B^{\top}]$.

In this section, we calculate $\mathbb{E}[\tilde{u}_B]$. For this, we need to use the $\text{clip}$ function to approximate the $\text{softsign}$ function:

Then we have

The integral form is complex, but it’s not difficult to calculate with Mathematica. The result can be expressed using the $\text{erf}$ function:

where $a = g\sqrt{B}/\sigma, b=\epsilon \sqrt{B}/\sigma$. This function appears complex, but it is precisely an S-shaped function of $a$, with a range of $(-1,1)$ and a slope of $\text{erf}(b/\sqrt{2})/b$ at $a=0$. Thus, using the first type of approximation:

The second approximate equality uses the approximation $\text{erf}(x)\approx x / \sqrt{x^2 + \pi / 4}$ to handle $\text{erf}(b/\sqrt{2})$ in the denominator. One might say we are quite fortunate that the final form is not too complicated. Then we have

As in the previous article, the last approximate equality uses the mean-field approximation, where $\kappa^2$ is some average of all $\sigma_i^2 /(g_i^2+\epsilon^2)$, and $u_i = \text{softsign}(g_i, \epsilon)$ and $\beta = (1 + \pi\kappa^2 / 2B)^{-1/2}$.

Variance Estimation

#

The mean, which is the first moment, is solved; now it’s time for the second moment:

The result can also be expressed using the $\text{erf}$ function, but it is much more verbose, so it won’t be written out here; again, for Mathematica, this is trivial. When viewed as a function of $a$, the result is an inverted bell-shaped curve, symmetric about the $y$-axis, with an upper bound of $1$, and a minimum within $(0,1)$. Referring to the approximation for $\mathbb{E}[\tilde{u}_B]$, we choose the following approximation:

To be fair, the precision of this approximation is not high; it’s primarily for computational convenience, but it retains key characteristics such as being inverted bell-shaped, symmetric about the $y$-axis, having an upper bound of 1, yielding 1 when $b=0$, and approaching 0 as $b\to\infty$. Next, we continue to apply the mean-field approximation:

Therefore, $\mathbb{E}[\tilde{\boldsymbol{u}}_B\tilde{\boldsymbol{u}}_B^{\top}]_{i,j}\approx u_i u_j \beta^2 + \delta_{i,j}(1-\beta^2)$. The term $\delta_{i,j}(1-\beta^2)$ represents the covariance matrix of $\tilde{\boldsymbol{u}}$, which is $(1-\beta^2)\boldsymbol{I}$. This is a diagonal matrix, which is expected, as one of our assumptions is the independence between the components of $\tilde{\boldsymbol{u}}$, so the covariance matrix must be diagonal.

Initial Results

#

From this, we obtain

Note that apart from $\beta$, all other symbols do not depend on $B$, so the above equation already provides the dependence of $\eta^*$ on $B$. Note that to ensure the existence of a minimum, we assume the positive definiteness of the $\boldsymbol{H}$ matrix, and under this assumption, it must be that $\sum_{i,j} u_i u_j H_{i,j} > 0$ and $\sum_i H_{i,i} > 0$.

In the previous article, we stated that Adam’s most important characteristic is the potential appearance of a “Surge phenomenon,” meaning that $\eta^*$ is no longer a globally monotonically increasing function with respect to $B$. Next, we will prove that the introduction of $\epsilon > 0$ reduces the probability of the Surge phenomenon occurring, and it completely disappears as $\epsilon \to \infty$. This proof is not difficult. It is clear that a necessary condition for the Surge phenomenon to appear is

Otherwise, the entire $\eta^*$ would be monotonically increasing with respect to $\beta$, and since $\beta$ is monotonically increasing with respect to $B$, the entire $\eta^*$ would be monotonically increasing with respect to $B$, and no Surge phenomenon would exist. Don’t forget that $u_i = \text{softsign}(g_i, \epsilon)$ is a monotonically decreasing function with respect to $\epsilon$. Therefore, as $\epsilon$ increases, $\sum_{i,j} u_i u_j H_{i,j}$ becomes smaller, making the above inequality less likely to hold. Furthermore, as $\epsilon\to \infty$, $u_i$ becomes zero, so the above inequality cannot hold, and thus the Surge phenomenon disappears.

Furthermore, we can prove that as $\epsilon\to\infty$, the result aligns with that of SGD. This only requires noting that

We have the limits:

Here, $\sigma^2$ is some average of all $\sigma_i^2$. Thus, we obtain the approximation when $\epsilon$ is sufficiently large:

The right-hand side is the SGD result when assuming the gradient covariance matrix is $(\pi\sigma^2/2B)\boldsymbol{I}$.

Summary (formatted)

#

This article continues the method from the previous article, attempting to analyze the impact of Adam’s $\epsilon$ on the scaling law between learning rate and Batch Size. The result is a form that interpolates between SGD and SignSGD: the larger $\epsilon$ is, the closer the result approaches SGD, and the lower the probability of the “Surge phenomenon” appearing. Overall, the computational results contain no particular surprises, but they can serve as a reference process for analyzing the effect of $\epsilon$.

@online{kexuefm-10563,
        title={How Adam's Epsilon Affects the Learning Rate Scaling Law?},
        author={苏剑林},
        year={2024},
        month={11},
        url={\url{https://kexue.fm/archives/10563}},
}