This is a gemini-2.5-flash translation of a Chinese article.
It has NOT been vetted for errors. You should have the original article open in a parallel tab at all times.
With the advent of the LLM era, the academic community’s enthusiasm for optimizer research seems to have waned. This is primarily because the current mainstream AdamW can satisfy most needs, and making “radical changes” to optimizers requires significant validation costs. Therefore, most changes to current optimizers are just small patches applied to AdamW by the industry based on their training experience.
However, a recent optimizer named “Muon” has garnered considerable attention on Twitter. It claims to be more efficient than AdamW and is not merely a “minor tweak” based on Adam, but rather embodies some thought-provoking principles regarding the differences between vectors and matrices. In this article, let’s appreciate it together.
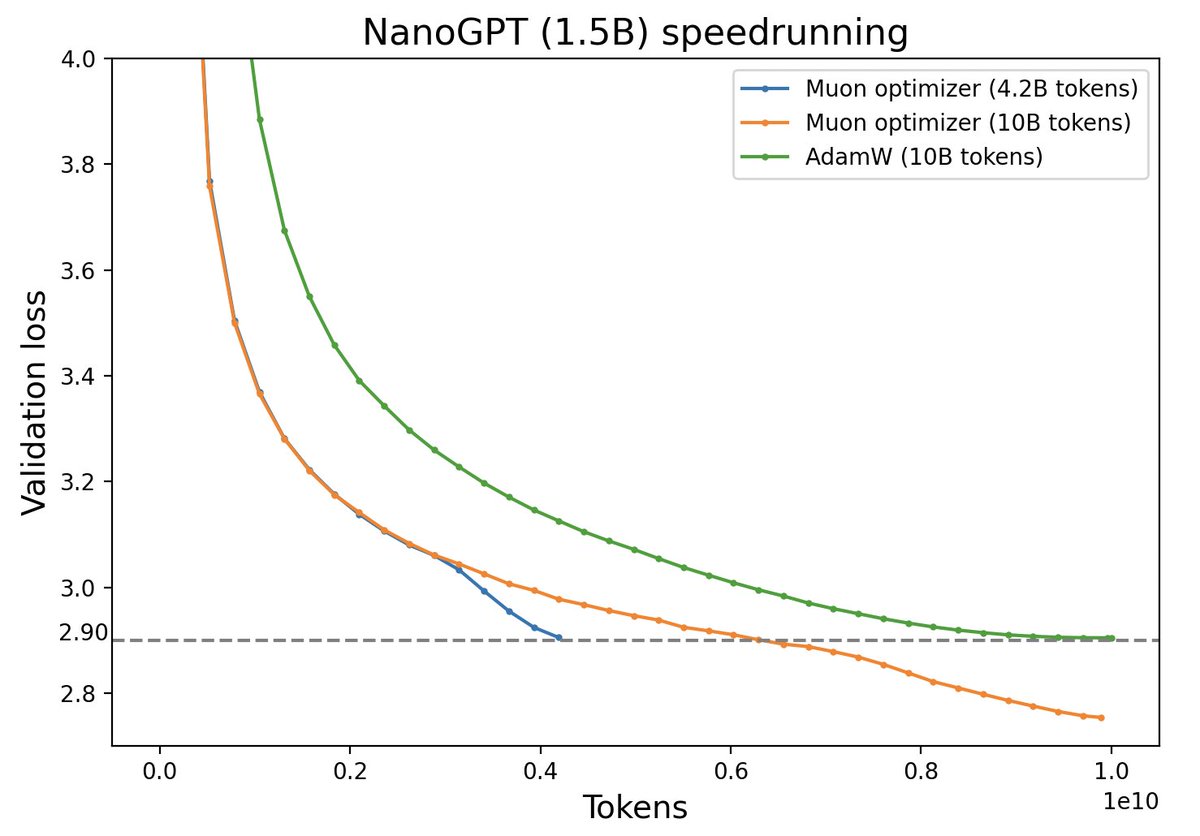
Comparison of Muon and AdamW performance (Source: Twitter @Yuchenj_UW)
Initial Exploration of the Algorithm#
Muon stands for “MomentUm Orthogonalized by Newton-schulz”. It is suitable for matrix parameters $\boldsymbol{W}\in\mathbb{R}^{n\times m}$, and its update rule is
$$ \begin{aligned} \boldsymbol{M}_t =&\, \beta\boldsymbol{M}_{t-1} + \boldsymbol{G}_t \\[5pt] \boldsymbol{W}_t =&\, \boldsymbol{W}_{t-1} - \eta_t [\text{msign}(\boldsymbol{M}_t) + \lambda \boldsymbol{W}_{t-1}] \\ \end{aligned} $$Here, $\text{msign}$ is the matrix sign function, which is not simply applying the $\text{sign}$ operation to each component of the matrix, but rather a matrix generalization of the $\text{sign}$ function. Its relationship with SVD is:
$$ \boldsymbol{U},\boldsymbol{\Sigma},\boldsymbol{V}^{\top} = \text{SVD}(\boldsymbol{M}) \quad\Rightarrow\quad \text{msign}(\boldsymbol{M}) = \boldsymbol{U}_{[:,:r]}\boldsymbol{V}_{[:,:r]}^{\top} $$where $\boldsymbol{U}\in\mathbb{R}^{n\times n},\boldsymbol{\Sigma}\in\mathbb{R}^{n\times m},\boldsymbol{V}\in\mathbb{R}^{m\times m}$, and $r$ is the rank of $\boldsymbol{M}$. We will elaborate on more theoretical details later; here, let’s first try to intuitively grasp the following fact:
Muon is an adaptive learning rate optimizer similar to Adam.
Adaptive learning rate optimizers like Adagrad, RMSprop, and Adam adjust the update amount for each parameter by dividing by the square root of the moving average of the squared gradient. This achieves two effects: 1. Constant scaling of the loss function does not affect the optimization trajectory; 2. The update magnitude for each parameter component is as consistent as possible. Muon perfectly satisfies these two characteristics:
- If the loss function is multiplied by $\lambda$, $\boldsymbol{M}$ will also be multiplied by $\lambda$, resulting in $\boldsymbol{\Sigma}$ being multiplied by $\lambda$. However, Muon’s final update amount transforms $\boldsymbol{\Sigma}$ into an identity matrix, so it does not affect the optimization result;
- When $\boldsymbol{M}$ is SVD-decomposed into $\boldsymbol{U}\boldsymbol{\Sigma}\boldsymbol{V}^{\top}$, the different singular values of $\boldsymbol{\Sigma}$ reflect the “anisotropy” of $\boldsymbol{M}$. Setting all of them to one makes it more isotropic and also serves to synchronize the update magnitudes.
By the way, regarding point 2, did any readers recall BERT-whitening? It’s also worth noting that Muon has a Nesterov version, which simply replaces $\text{msign}(\boldsymbol{M}_t)$ in the update rule with $\text{msign}(\beta\boldsymbol{M}_t + \boldsymbol{G}_t)$, with the rest being identical. For simplicity, it won’t be elaborated on here.
(Archaeology: It was later discovered that the 2015 paper 《Stochastic Spectral Descent for Restricted Boltzmann Machines》 had already proposed an optimization algorithm largely similar to Muon, then called “Stochastic Spectral Descent”.)
Sign Function#
Using SVD, we can also prove the identity
$$ \text{msign}(\boldsymbol{M}) = (\boldsymbol{M}\boldsymbol{M}^{\top})^{-1/2}\boldsymbol{M}= \boldsymbol{M}(\boldsymbol{M}^{\top}\boldsymbol{M})^{-1/2} $$where ${}^{-1/2}$ denotes the inverse of the matrix’s $1/2$ power, or the pseudoinverse if it’s not invertible. This identity helps us better understand why $\text{msign}$ is a matrix generalization of $\text{sign}$: For a scalar $x$, we have $\text{sign}(x)=x(x^2)^{-1/2}$, which is a special case of the above equation (when $\boldsymbol{M}$ is a $1\times 1$ matrix). This special case can also be generalized to a diagonal matrix $\boldsymbol{M}=\text{diag}(\boldsymbol{m})$:
$$ \text{msign}(\boldsymbol{M}) = \text{diag}(\boldsymbol{m})[\text{diag}(\boldsymbol{m})^2]^{-1/2} = \text{diag}(\text{sign}(\boldsymbol{m}))=\text{sign}(\boldsymbol{M}) $$Here, $\text{sign}(\boldsymbol{m})$ and $\text{sign}(\boldsymbol{M})$ refer to applying $\text{sign}$ to each component of the vector/matrix. The above equation implies that when $\boldsymbol{M}$ is a diagonal matrix, Muon degenerates into SignSGD (Signum) with momentum, or the Tiger optimizer proposed by the author, both of which are classic approximations of Adam. Conversely, the difference between Muon and Signum/Tiger is that the element-wise $\text{sign}(\boldsymbol{M})$ is replaced by the matrix version $\text{msign}(\boldsymbol{M})$.
For an $n$-dimensional vector, we can also view it as an $n\times 1$ matrix. In this case, $\text{msign}(\boldsymbol{m}) = \boldsymbol{m}/\Vert\boldsymbol{m}\Vert_2$ is precisely $l_2$ normalization. Therefore, within the Muon framework, we have two perspectives on vectors: one as a diagonal matrix, such as the gamma parameter of LayerNorm, where the result is taking the $\text{sign}$ of the momentum; the other as an $n\times 1$ matrix, where the result is $l_2$ normalization of the momentum. Furthermore, although input and output Embeddings are also matrices, they are used sparsely, so a more reasonable approach is to treat them as multiple vectors and process them independently.
When $m=n=r$, $\text{msign}(\boldsymbol{M})$ also has the meaning of “optimal orthogonal approximation”:
$$ \text{msign}(\boldsymbol{M}) = \mathop{\text{argmin}}_{\boldsymbol{O}^{\top}\boldsymbol{O} = \boldsymbol{I}}\Vert \boldsymbol{M} - \boldsymbol{O}\Vert_F^2 $$Similarly, for $\text{sign}(\boldsymbol{M})$ we can write (assuming $\boldsymbol{M}$ has no zero elements):
$$ \text{sign}(\boldsymbol{M}) = \mathop{\text{argmin}}_{\boldsymbol{O}\in\{-1,1\}^{n\times m}}\Vert \boldsymbol{M} - \boldsymbol{O}\Vert_F^2 $$Whether it’s $\boldsymbol{O}^{\top}\boldsymbol{O} = \boldsymbol{I}$ or $\boldsymbol{O}\in\{-1,1\}^{n\times m}$, both can be regarded as a regularization constraint on the update amount. Thus, Muon, Signum, and Tiger can be seen as optimizers under the same idea: they all construct the update amount starting from momentum $\boldsymbol{M}$, but choose different regularization methods for the update amount.
$$ \begin{aligned} \Vert \boldsymbol{M} - \boldsymbol{O}\Vert_F^2 =&\, \Vert \boldsymbol{M}\Vert_F^2 + \Vert \boldsymbol{O}\Vert_F^2 - 2\langle\boldsymbol{M},\boldsymbol{O}\rangle_F \\[5pt] =&\, \Vert \boldsymbol{M}\Vert_F^2 + n - 2\text{Tr}(\boldsymbol{M}\boldsymbol{O}^{\top})\\[5pt] =&\, \Vert \boldsymbol{M}\Vert_F^2 + n - 2\text{Tr}(\boldsymbol{U}\boldsymbol{\Sigma}\boldsymbol{V}^{\top}\boldsymbol{O}^{\top})\\[5pt] =&\, \Vert \boldsymbol{M}\Vert_F^2 + n - 2\text{Tr}(\boldsymbol{\Sigma}\boldsymbol{V}^{\top}\boldsymbol{O}^{\top}\boldsymbol{U})\\ =&\, \Vert \boldsymbol{M}\Vert_F^2 + n - 2\sum_{i=1}^n \boldsymbol{\Sigma}_{i,i}(\boldsymbol{V}^{\top}\boldsymbol{O}^{\top}\boldsymbol{U})_{i,i} \end{aligned} $$Proof of Equation (nearest-orth): For an orthogonal matrix $\boldsymbol{O}$, we have
The operation rules involved here have been introduced in our article on pseudoinverse. Since $\boldsymbol{U},\boldsymbol{V},\boldsymbol{O}$ are all orthogonal matrices, $\boldsymbol{V}^{\top}\boldsymbol{O}^{\top}\boldsymbol{U}$ is also an orthogonal matrix. Each component of an orthogonal matrix must not exceed 1. Also, because $\boldsymbol{\Sigma}_{i,i} > 0$, the minimum of the above expression corresponds to each $(\boldsymbol{V}^{\top}\boldsymbol{O}^{\top}\boldsymbol{U})_{i,i}$ taking its maximum value, i.e., $(\boldsymbol{V}^{\top}\boldsymbol{O}^{\top}\boldsymbol{U})_{i,i}=1$. This implies $\boldsymbol{V}^{\top}\boldsymbol{O}^{\top}\boldsymbol{U}=\boldsymbol{I}$, which means $\boldsymbol{O}=\boldsymbol{U}\boldsymbol{V}^{\top}$.
This conclusion can also be carefully extended to cases where $m,n,r$ are not equal, but we will not delve further into that here.
Iterative Solution#
In practice, if SVD is performed on $\boldsymbol{M}$ at each step to solve for $\text{msign}(\boldsymbol{M})$, the computational cost would be relatively high. Therefore, the authors proposed using Newton-Schulz iteration to approximate $\text{msign}(\boldsymbol{M})$.
The starting point for the iteration is identity (msign-id). Without loss of generality, let’s assume $n\geq m$. Then, consider the Taylor expansion of $(\boldsymbol{M}^{\top}\boldsymbol{M})^{-1/2}$ around $\boldsymbol{M}^{\top}\boldsymbol{M}=\boldsymbol{I}$. The expansion method directly applies the result of the scalar function $t^{-1/2}$ to matrices:
$$ t^{-1/2} = 1 - \frac{1}{2}(t-1) + \frac{3}{8}(t-1)^2 - \frac{5}{16}(t-1)^3 + \cdots $$Keeping up to the second order, the result is $(15 - 10t + 3t^2)/8$. Thus, we have
$$ \text{msign}(\boldsymbol{M}) = \boldsymbol{M}(\boldsymbol{M}^{\top}\boldsymbol{M})^{-1/2}\approx \frac{15}{8}\boldsymbol{M} - \frac{5}{4}\boldsymbol{M}(\boldsymbol{M}^{\top}\boldsymbol{M}) + \frac{3}{8}\boldsymbol{M}(\boldsymbol{M}^{\top}\boldsymbol{M})^2 $$If $\boldsymbol{X}_t$ is an approximation of $\text{msign}(\boldsymbol{M})$, we assume that substituting it into the above equation will yield a better approximation of $\text{msign}(\boldsymbol{M})$. This gives us a usable iterative format:
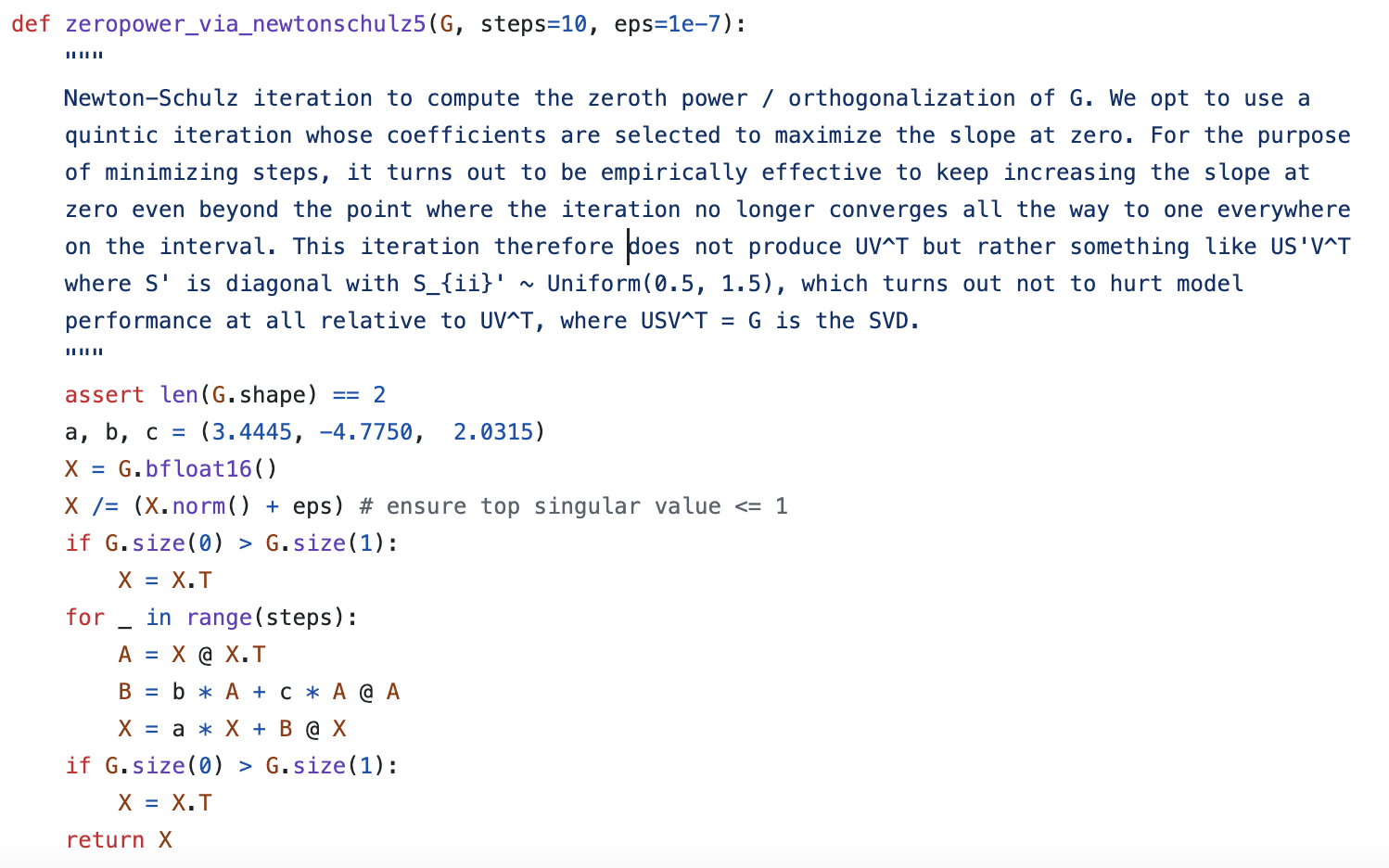
$$ \boldsymbol{X}_{t+1} = \frac{15}{8}\boldsymbol{X}_t - \frac{5}{4}\boldsymbol{X}_t(\boldsymbol{X}_t^{\top}\boldsymbol{X}_t) + \frac{3}{8}\boldsymbol{X}_t(\boldsymbol{X}_t^{\top}\boldsymbol{X}_t)^2 $$However, upon examining Muon’s official code, we find that its Newton-Schulz iteration indeed follows this form, but the three coefficients are $(3.4445, -4.7750, 2.0315)$. Moreover, the authors did not provide a mathematical derivation, only a vague comment:
Newton-Schulz iteration of Muon optimizer
Convergence Acceleration#
To guess the source of the official iterative algorithm, let’s consider a general iterative process:
$$ \boldsymbol{X}_{t+1} = a\boldsymbol{X}_t + b\boldsymbol{X}_t(\boldsymbol{X}_t^{\top}\boldsymbol{X}_t) + c\boldsymbol{X}_t(\boldsymbol{X}_t^{\top}\boldsymbol{X}_t)^2 $$where $a,b,c$ are three coefficients to be solved. If a higher-order iterative algorithm is desired, we can sequentially add terms like $\boldsymbol{X}_t(\boldsymbol{X}_t^{\top}\boldsymbol{X}_t)^3$, $\boldsymbol{X}_t(\boldsymbol{X}_t^{\top}\boldsymbol{X}_t)^4$, etc. The following analysis process is general.
The initial value we choose is $\boldsymbol{X}_0=\boldsymbol{M}/\Vert\boldsymbol{M}\Vert_F$, where $\Vert\cdot\Vert_F$ is the Frobenius norm of the matrix. The rationale for this choice is that dividing by $\Vert\boldsymbol{M}\Vert_F$ does not change the $\boldsymbol{U},\boldsymbol{V}$ of the SVD, but it ensures that all singular values of $\boldsymbol{X}_0$ are within $[0,1]$, making the initial singular values for the iteration more standardized. Now, assuming $\boldsymbol{X}_t$ can be SVD-decomposed into $\boldsymbol{U}\boldsymbol{\Sigma}_t\boldsymbol{V}^{\top}$, then substituting it into the above equation, we can obtain
$$ \boldsymbol{X}_{t+1} = \boldsymbol{U}_{[:,:r]}(a \boldsymbol{\Sigma}_{t,[:r,:r]} + b \boldsymbol{\Sigma}_{t,[:r,:r]}^3 + c \boldsymbol{\Sigma}_{t,[:r,:r]}^5)\boldsymbol{V}_{[:,:r]}^{\top} $$Therefore, Equation (iteration) is actually iterating on the diagonal matrix $\boldsymbol{\Sigma}_{[:r,:r]}$ composed of singular values. If we denote $\boldsymbol{X}_t=\boldsymbol{U}_{[:,:r]}\boldsymbol{\Sigma}_{t,[:r,:r]}\boldsymbol{V}_{[:,:r]}^{\top}$, then we have $\boldsymbol{\Sigma}_{t+1,[:r,:r]} = g(\boldsymbol{\Sigma}_{t,[:r,:r]})$, where $g(x) = ax + bx^3 + cx^5$. Furthermore, since the power of a diagonal matrix equals the power of its diagonal elements, the problem simplifies to the iteration of a single singular value $\sigma$. Our goal is to compute $\boldsymbol{U}_{[:,:r]}\boldsymbol{V}_{[:,:r]}^{\top}$. In other words, we hope to transform $\boldsymbol{\Sigma}_{[:r,:r]}$ into an identity matrix through iteration. This can further be simplified to iterating $\sigma_{t+1} = g(\sigma_t)$ to change a single singular value to 1.
Inspired by @leloykun, we treat the choice of $a,b,c$ as an optimization problem, aiming to make the iterative process converge as quickly as possible for any initial singular value. First, we re-parameterize $g(x)$ as
$$ g(x) = x + \kappa x(x^2 - x_1^2)(x^2 - x_2^2) $$where $x_1 \leq x_2$. The advantage of this parameterization is that it directly shows the five fixed points of the iteration: $0,\pm x_1,\pm x_2$. Since our goal is to converge to 1, we initialize with $x_1 < 1, x_2 > 1$. The idea is that no matter whether the iteration moves towards $x_1$ or $x_2$, the result will be close to 1.
Next, we determine the number of iteration steps $T$, making the iterative process a deterministic function. Then, after fixing the matrix shape (i.e., $n,m$), we can sample a batch of matrices and compute their singular values via SVD. Finally, we treat these singular values as input, with the target output being 1. The loss function is squared error. The entire model is fully differentiable and can be solved using gradient descent (@leloykun assumed $x_1 + x_2 = 2$ and then used grid search to solve).
Some computation results:
| $n$ | $m$ | $T$ | $\kappa$ | $x_1$ | $x_2$ | $a$ | $b$ | $c$ | $\text{mse}$ | $\text{mse}_{\text{o}}$ |
|---|---|---|---|---|---|---|---|---|---|---|
| 1024 | 1024 | 3 | 7.020 | 0.830 | 0.830 | 4.328 | -9.666 | 7.020 | 0.10257 | 0.18278 |
| 1024 | 1024 | 5 | 1.724 | 0.935 | 1.235 | 3.297 | -4.136 | 1.724 | 0.02733 | 0.04431 |
| 2048 | 1024 | 3 | 7.028 | 0.815 | 0.815 | 4.095 | -9.327 | 7.028 | 0.01628 | 0.06171 |
| 2048 | 1024 | 5 | 1.476 | 0.983 | 1.074 | 2.644 | -3.128 | 1.476 | 0.00038 | 0.02954 |
| 4096 | 1024 | 3 | 6.948 | 0.802 | 0.804 | 3.886 | -8.956 | 6.948 | 0.00371 | 0.02574 |
| 4096 | 1024 | 5 | 1.214 | 1.047 | 1.048 | 2.461 | -2.663 | 1.214 | 0.00008 | 0.02563 |
| 2048 | 2048 | 3 | 11.130 | 0.767 | 0.767 | 4.857 | -13.103 | 11.130 | 0.10739 | 0.24410 |
| 2048 | 2048 | 5 | 1.779 | 0.921 | 1.243 | 3.333 | -4.259 | 1.779 | 0.03516 | 0.04991 |
| 4096 | 4096 | 3 | 18.017 | 0.705 | 0.705 | 5.460 | -17.929 | 18.017 | 0.11303 | 0.33404 |
| 4096 | 4096 | 5 | 2.057 | 0.894 | 1.201 | 3.373 | -4.613 | 2.057 | 0.04700 | 0.06372 |
| 8192 | 8192 | 3 | 30.147 | 0.643 | 0.643 | 6.139 | -24.893 | 30.147 | 0.11944 | 0.44843 |
| 8192 | 8192 | 5 | 2.310 | 0.871 | 1.168 | 3.389 | -4.902 | 2.310 | 0.05869 | 0.07606 |
Here, $\text{mse}_{\text{o}}$ is the result calculated using the $a,b,c$ coefficients provided by the Muon authors. From the table, it can be seen that the results are clearly related to matrix size and the number of iteration steps; in terms of the loss function, non-square matrices converge more easily than square matrices; the $a,b,c$ given by the Muon authors are likely the optimal solution for square matrices when the number of iteration steps is 5. When the number of iteration steps is fixed, the results depend on the matrix size, which essentially depends on the distribution of singular values. Regarding this distribution, it’s worth noting that when $n,m\to\infty$, it follows the Marchenko–Pastur distribution.
Reference code:
import jax
import jax.numpy as jnp
from tqdm import tqdm
n, m, T = 1024, 1024, 5
key, data = jax.random.key(42), jnp.array([])
for _ in tqdm(range(1000), ncols=0, desc='SVD'):
key, subkey = jax.random.split(key)
M = jax.random.normal(subkey, shape=(n, m))
S = jnp.linalg.svd(M, full_matrices=False)[1]
data = jnp.concatenate([data, S / (S**2).sum()**0.5])
@jax.jit
def f(w, x):
k, x1, x2 = w
for _ in range(T):
x = x + k * x * (x**2 - x1**2) * (x**2 - x2**2)
return ((x - 1)**2).mean()
f_grad = jax.grad(f)
w, u = jnp.array([1, 0.9, 1.1]), jnp.zeros(3)
for _ in tqdm(range(100000), ncols=0, desc='SGD'):
u = 0.9 * u + f_grad(w, data) # 动量加速
w = w - 0.01 * u
k, x1, x2 = w
a, b, c = 1 + k * x1**2 * x2**2, -k * (x1**2 + x2**2), k
print(f'{n} & {m} & {T} & {k:.3f} & {x1:.3f} & {x2:.3f} & {a:.3f} & {b:.3f} & {c:.3f} & {f(w, data):.5f}')
Some Thoughts#
If we follow the default choice of $T=5$, then for an $n\times n$ matrix parameter, each Muon update step requires at least 15 $n\times n$ matrix multiplications. This computational load is undoubtedly significantly larger than Adam’s, which might lead readers to wonder if Muon is practical.
In fact, such worries are superfluous. Although Muon’s computation is more complex than Adam’s, the additional time per step is not significant. My conclusion is within 5%, while the Muon authors claim it can be as low as 2%. This is because Muon’s matrix multiplications occur after the current gradient computation and before the next one. During this period, almost all computational resources are idle. These matrix multiplications are of static size and can be parallelized, hence they do not significantly increase time costs. On the contrary, Muon uses one fewer set of cached variables than Adam, resulting in lower VRAM costs.
The most thought-provoking aspect of Muon is actually the inherent difference between vectors and matrices, and its impact on optimization. Common optimizers like SGD, Adam, and Tiger have element-wise update rules. This means that regardless of whether the parameters are vectors or matrices, they are essentially treated as one large vector, with components updated independently according to the same rule. Optimizers with this characteristic are often simpler to analyze theoretically and facilitate tensor parallelism, because splitting a large matrix into two smaller matrices and processing them independently does not change the optimization trajectory.
Muon, however, is different. It treats matrices as fundamental units and considers some of their unique characteristics. Some readers might wonder: Aren’t matrices and vectors just arrangements of numbers? What could be the difference? For example, in matrices, we have the concept of “trace”, which is the sum of diagonal elements. This concept is not arbitrarily defined; it has an important property of remaining invariant under similarity transformations, and it also equals the sum of all eigenvalues of the matrix. From this example, it can be seen that the diagonal elements and off-diagonal elements of a matrix are not entirely equal in status. And it is precisely because Muon considers this asymmetry that it achieves better results.
Of course, this also leads to some negative impacts. If a matrix is distributed across different devices, then when using Muon, their gradients need to be aggregated before calculating the update amount, rather than allowing each device to update independently. This increases communication cost. Even if we don’t consider parallelism, this problem still exists. For instance, Multi-Head Attention typically projects onto $Q$ (and $K,V$ similarly) via a single large matrix, then uses reshaping to obtain multiple Heads. This means there’s only a single matrix in the model parameters, but it’s essentially multiple small matrices. Therefore, ideally, we should split the large matrix into multiple small matrices and update them independently.
In summary, Muon’s non-element-wise update rule, while capturing the fundamental differences between vectors and matrices, also introduces some minor issues, which might not appeal to all readers.
(Addendum: Almost simultaneously with the publication of this blog post, Muon’s author, Keller Jordan, also released his own blog post 《Muon: An optimizer for hidden layers in neural networks》.)
Norm Perspective#
From a theoretical standpoint, what key properties of matrices does Muon capture? Perhaps the following norm perspective can answer our question.
The discussion in this section primarily references the papers 《Stochastic Spectral Descent for Discrete Graphical Models》 and 《Old Optimizer, New Norm: An Anthology》, especially the latter. However, the starting point is not new; we have already briefly touched upon it in 《Gradient Flow: Exploring the Path to Minimum》: For vector parameters $\boldsymbol{w}\in\mathbb{R}^n$, we define the next update rule as
$$ \boldsymbol{w}_{t+1} = \mathop{\text{argmin}}_{\boldsymbol{w}} \frac{\Vert\boldsymbol{w} - \boldsymbol{w}_t\Vert^2}{2\eta_t} + \mathcal{L}(\boldsymbol{w}) $$where $\Vert\Vert$ is a certain vector norm. This is called “steepest gradient descent” under a certain norm constraint. Assuming $\eta_t$ is sufficiently small, the first term dominates, meaning $\boldsymbol{w}_{t+1}$ will be very close to $\boldsymbol{w}_t$. Thus, we assume that the first-order approximation of $\mathcal{L}(\boldsymbol{w})$ is sufficient, and the problem simplifies to
$$ \boldsymbol{w}_{t+1} = \mathop{\text{argmin}}_{\boldsymbol{w}} \frac{\Vert\boldsymbol{w} - \boldsymbol{w}_t\Vert^2}{2\eta_t} + \mathcal{L}(\boldsymbol{w}_t) + \nabla_{\boldsymbol{w}_t}\mathcal{L}(\boldsymbol{w}_t)^{\top}(\boldsymbol{w}-\boldsymbol{w}_t) $$Let $\Delta\boldsymbol{w}_{t+1} = \boldsymbol{w}_{t+1}-\boldsymbol{w}_t$ and $\boldsymbol{g}_t = \nabla_{\boldsymbol{w}_t}\mathcal{L}(\boldsymbol{w}_t)$. Then it can be abbreviated as
$$ \Delta\boldsymbol{w}_{t+1} = \mathop{\text{argmin}}_{\Delta\boldsymbol{w}} \frac{\Vert\Delta\boldsymbol{w}\Vert^2}{2\eta_t} + \boldsymbol{g}_t^{\top}\Delta\boldsymbol{w} $$The general approach to computing $\Delta\boldsymbol{w}_{t+1}$ is by taking derivatives, but 《Old Optimizer, New Norm: An Anthology》 provides a unified approach that doesn’t require differentiation: decompose $\Delta\boldsymbol{w}$ into its norm $\gamma = \Vert\Delta\boldsymbol{w}\Vert$ and direction vector $\boldsymbol{\phi} = -\Delta\boldsymbol{w}/\Vert\Delta\boldsymbol{w}\Vert$. Thus,
$$ \min_{\Delta\boldsymbol{w}} \frac{\Vert\Delta\boldsymbol{w}\Vert^2}{2\eta_t} + \boldsymbol{g}_t^{\top}\Delta\boldsymbol{w} = \min_{\gamma\geq 0, \Vert\boldsymbol{\phi}\Vert=1} \frac{\gamma^2}{2\eta_t} - \gamma\boldsymbol{g}_t^{\top}\boldsymbol{\phi} = \min_{\gamma\geq 0} \frac{\gamma^2}{2\eta_t} - \gamma\bigg(\underbrace{\max_{\Vert\boldsymbol{\phi}\Vert=1}\boldsymbol{g}_t^{\top}\boldsymbol{\phi}}_{\text{denoted as}\Vert \boldsymbol{g}_t\Vert^{\dagger}}\bigg) $$$\gamma$ is merely a scalar, similar to the learning rate, and its optimal value is easily found to be $\eta_t\Vert \boldsymbol{g}_t\Vert^{\dagger}$. The update direction is $\boldsymbol{\phi}^*$ that maximizes $\boldsymbol{g}_t^{\top}\boldsymbol{\phi}$ (where $\Vert\boldsymbol{\phi}\Vert=1$). Now, substituting the Euclidean norm, i.e., $\Vert\boldsymbol{\phi}\Vert_2 = \sqrt{\boldsymbol{\phi}^{\top}\boldsymbol{\phi}}$, we get $\Vert \boldsymbol{g}_t\Vert^{\dagger}=\Vert \boldsymbol{g}_t\Vert_2$ and $\boldsymbol{\phi}^* = \boldsymbol{g}_t/\Vert\boldsymbol{g}_t\Vert_2$. This yields $\Delta\boldsymbol{w}_{t+1}=-\eta_t \boldsymbol{g}_t$, which is gradient descent (SGD). In general, for the $p$-norm
$$ \Vert\boldsymbol{\phi}\Vert_p = \sqrt[p]{\sum_{i=1}^n |\phi_i|^p} $$Hölder’s inequality gives $\boldsymbol{g}^{\top}\boldsymbol{\phi} \leq \Vert \boldsymbol{g}\Vert_q \Vert \boldsymbol{\phi}\Vert_p$, where $1/p + 1/q = 1$. Using it, we obtain
$$ \max_{\Vert\boldsymbol{\phi}\Vert_p=1}\boldsymbol{g}^{\top}\boldsymbol{\phi} = \Vert \boldsymbol{g}\Vert_q $$The condition for equality to hold is
$$ \boldsymbol{\phi}^* = \frac{1}{\Vert\boldsymbol{g}\Vert_q^{q/p}}\Big[\text{sign}(g_1) |g_1|^{q/p},\text{sign}(g_2) |g_2|^{q/p},\cdots,\text{sign}(g_n) |g_n|^{q/p}\Big] $$The optimizer using this as its direction vector is called pbSGD; refer to 《pbSGD: Powered Stochastic Gradient Descent Methods for Accelerated Non-Convex Optimization》. In particular, when $p\to\infty$, we have $q\to 1$ and $|g_i|^{q/p}\to 1$. In this case, it degenerates to SignSGD, meaning SignSGD is actually the steepest gradient descent under the $\Vert\Vert_{\infty}$ norm.
Matrix Norms#
Now let’s turn our attention to matrix parameters $\boldsymbol{W}\in\mathbb{R}^{n\times m}$. Similarly, we define its update rule as
$$ \boldsymbol{W}_{t+1} = \mathop{\text{argmin}}_{\boldsymbol{W}} \frac{\Vert\boldsymbol{W} - \boldsymbol{W}_t\Vert^2}{2\eta_t} + \mathcal{L}(\boldsymbol{W}) $$Here, $\Vert\Vert$ is a certain matrix norm. Using the first-order approximation again, we obtain
$$ \Delta\boldsymbol{W}_{t+1} = \mathop{\text{argmin}}_{\Delta\boldsymbol{W}} \frac{\Vert\Delta\boldsymbol{W}\Vert^2}{2\eta_t} + \text{Tr}(\boldsymbol{G}_t^{\top}\Delta\boldsymbol{W}) $$Here, $\Delta\boldsymbol{W}_{t+1} = \boldsymbol{W}_{t+1}-\boldsymbol{W}_t$ and $\boldsymbol{G}_t = \nabla_{\boldsymbol{W}_t}\mathcal{L}(\boldsymbol{W}_t)$. Still using the “norm-direction” decoupling, i.e., let $\gamma = \Vert\Delta\boldsymbol{W}\Vert$ and $\boldsymbol{\Phi} = -\Delta\boldsymbol{W}/\Vert\Delta\boldsymbol{W}\Vert$, we obtain
$$ \min_{\Delta\boldsymbol{W}} \frac{\Vert\Delta\boldsymbol{W}\Vert^2}{2\eta_t} + \text{Tr}(\boldsymbol{G}_t^{\top}\Delta\boldsymbol{W}) = \min_{\gamma\geq 0} \frac{\gamma^2}{2\eta_t} - \gamma\bigg(\underbrace{\max_{\Vert\boldsymbol{\Phi}\Vert=1}\text{Tr}(\boldsymbol{G}_t^{\top}\boldsymbol{\Phi})}_{\text{denoted as}\Vert \boldsymbol{G}_t\Vert^{\dagger}}\bigg) $$Then it comes down to analyzing specific norms. There are two commonly used matrix norms. One is the Frobenius norm, which is essentially the Euclidean norm calculated after flattening the matrix into a vector. In this case, the conclusion is the same as for vectors, and the answer is SGD, so we won’t elaborate further here; the other is the $2$-norm, also known as the spectral norm, induced from vector norms:
$$ \Vert \boldsymbol{\Phi}\Vert_2 = \max_{\Vert \boldsymbol{x}\Vert_2 = 1} \Vert \boldsymbol{\Phi}\boldsymbol{x}\Vert_2 $$Note that the objects appearing in $\Vert\Vert_2$ on the right side are all vectors, so the definition is clear. More discussion on the $2$-norm can be found in 《Lipschitz Constraints in Deep Learning: Generalization and Generative Models》 and 《The Path of Low-Rank Approximation (II): SVD》. Since the $2$-norm is induced by “matrix-vector” multiplication, it aligns better with matrix multiplication, and it always holds that $\Vert\boldsymbol{\Phi}\Vert_2\leq \Vert\boldsymbol{\Phi}\Vert_F$, meaning the $2$-norm is tighter than the Frobenius norm.
Therefore, we will now compute for the $2$-norm. Let the SVD of $\boldsymbol{G}$ be $\boldsymbol{U}\boldsymbol{\Sigma}\boldsymbol{V}^{\top} = \sum\limits_{i=1}^r \sigma_i \boldsymbol{u}_i \boldsymbol{v}_i^{\top}$. We have
$$ \text{Tr}(\boldsymbol{G}^{\top}\boldsymbol{\Phi})=\text{Tr}\Big(\sum_{i=1}^r \sigma_i \boldsymbol{v}_i \boldsymbol{u}_i^{\top}\boldsymbol{\Phi}\Big) = \sum_{i=1}^r \sigma_i \boldsymbol{u}_i^{\top}\boldsymbol{\Phi}\boldsymbol{v}_i $$By definition, when $\Vert\boldsymbol{\Phi}\Vert_2=1$, $\Vert\boldsymbol{\Phi}\boldsymbol{v}_i\Vert_2\leq \Vert\boldsymbol{v}_i\Vert_2=1$, so $\boldsymbol{u}_i^{\top}\boldsymbol{\Phi}\boldsymbol{v}_i\leq 1$. Therefore,
$$ \text{Tr}(\boldsymbol{G}^{\top}\boldsymbol{\Phi})\leq \sum_{i=1}^r \sigma_i $$Equality holds when all $\boldsymbol{u}_i^{\top}\boldsymbol{\Phi}\boldsymbol{v}_i$ are equal to 1, at which point
$$ \boldsymbol{\Phi} = \sum_{i=1}^r \boldsymbol{u}_i \boldsymbol{v}_i^{\top} = \boldsymbol{U}_{[:,:r]}\boldsymbol{V}_{[:,:r]}^{\top} = \text{msign}(\boldsymbol{G}) $$Thus, we have proved that gradient descent under $2$-norm regularization is precisely the Muon optimizer when $\beta=0$! When $\beta > 0$, the moving average takes effect, and we can regard it as a more precise estimate of the gradient, so $\text{msign}$ is applied to the momentum instead. In summary, Muon is equivalent to gradient descent under a $2$-norm constraint. The $2$-norm better measures the intrinsic differences between matrices, leading to more precise and fundamental steps in optimization.
Tracing the Roots#
Muon also has an older related work, 《Shampoo: Preconditioned Stochastic Tensor Optimization》, a 2018 paper that proposed an optimizer named Shampoo, which shares similarities with Muon.
Adam’s strategy of adapting learning rates through the average of squared gradients was first proposed in the Adagrad paper 《Adaptive Subgradient Methods for Online Learning and Stochastic Optimization》, which suggested a strategy of directly accumulating squared gradients, equivalent to a globally equally weighted average. Later, RMSProp and Adam, by analogy with the design of momentum, switched to moving averages and found better practical performance.
Furthermore, what Adagrad originally proposed was actually accumulating the outer product $\boldsymbol{g}\boldsymbol{g}^{\top}$. However, caching outer products incurred too much spatial cost, so in practice, it was replaced by the Hadamard product $\boldsymbol{g}\odot\boldsymbol{g}$. So, what is the theoretical basis for accumulating outer products? We derived this in 《Adaptive Learning Rate Optimizers from a Hessian Approximation Perspective》. The answer is that “the long-term average of the gradient outer product $\mathbb{E}[\boldsymbol{g}\boldsymbol{g}^{\top}]$ approximates the square of the Hessian matrix $\sigma^2\boldsymbol{\mathcal{H}}_{\boldsymbol{\theta}^*}^2$,” so this is essentially approximating a second-order Newton method.
Shampoo inherited Adagrad’s idea of caching outer products, but considering cost issues, it adopted a compromise. Like Muon, it also optimizes for matrices (and higher-order tensors). The strategy is to cache matrix products of gradients, $\boldsymbol{G}\boldsymbol{G}^{\top}$ and $\boldsymbol{G}^{\top}\boldsymbol{G}$, instead of outer products, such that the spatial cost is $\mathcal{O}(n^2 + m^2)$ rather than $\mathcal{O}(n^2 m^2)$:
$$ \begin{aligned} \boldsymbol{L}_t =&\, \beta\boldsymbol{L}_{t-1} + \boldsymbol{G}_t\boldsymbol{G}_t^{\top} \\[5pt] \boldsymbol{R}_t =&\, \beta\boldsymbol{R}_{t-1} + \boldsymbol{G}_t^{\top}\boldsymbol{G}_t \\[5pt] \boldsymbol{W}_t =&\, \boldsymbol{W}_{t-1} - \eta_t \boldsymbol{L}_t^{-1/4}\boldsymbol{G}_t\boldsymbol{R}_t^{-1/4} \\ \end{aligned} $$The $\beta$ here was added by the author; Shampoo defaults to $\beta=1$. ${}^{-1/4}$ is also a matrix power operation, which can be performed using SVD. Since Shampoo did not propose approximation schemes like Newton-Schulz iteration and computes directly using SVD, to save computational cost, it does not calculate $\boldsymbol{L}_t^{-1/4}$ and $\boldsymbol{R}_t^{-1/4}$ at every step, but rather updates their results at certain intervals.
In particular, when $\beta=0$, Shampoo’s update vector is $(\boldsymbol{G}\boldsymbol{G}^{\top})^{-1/4}\boldsymbol{G}(\boldsymbol{G}^{\top}\boldsymbol{G})^{-1/4}$. By performing SVD on $\boldsymbol{G}$, we can prove that
$$ (\boldsymbol{G}\boldsymbol{G}^{\top})^{-1/4}\boldsymbol{G}(\boldsymbol{G}^{\top}\boldsymbol{G})^{-1/4} = (\boldsymbol{G}\boldsymbol{G}^{\top})^{-1/2}\boldsymbol{G}= \boldsymbol{G}(\boldsymbol{G}^{\top}\boldsymbol{G})^{-1/2}=\text{msign}(\boldsymbol{G}) $$This indicates that when $\beta=0$, Shampoo and Muon are theoretically equivalent! Therefore, Shampoo and Muon share commonalities in the design of their update amounts.
Summary (formatted)#
This article introduced the recently popular Muon optimizer on Twitter. It is specially designed for matrix parameters, appears to be more efficient than AdamW, and seems to embody some fundamental differences between vectorization and matrixization, making it worth studying and pondering.
@online{kexuefm-10592,
title={An Appreciation of Muon Optimizer: A Fundamental Leap from Vectors to Matrices},
author={苏剑林},
year={2024},
month={12},
url={\url{https://kexue.fm/archives/10592}},
}