Why Did We Choose to Try Muon?

This article interprets our latest technical report 《Muon is Scalable for LLM Training》, which shares a large-scale practice of the Muon optimizer that we previously introduced in 《Appreciation of Muon Optimizer: An Essential Leap from Vectors to Matrices》, and open-sourced the corresponding model (which we call “Moonlight”, currently a 3B/16B MoE model). We found a rather surprising conclusion: under our experimental setup, Muon can achieve nearly 2 times the training efficiency compared to Adam.

The work of optimizers is neither abundant nor scarce. Why did we choose Muon as a new direction to try? How can we quickly switch from a well-tuned Adam optimizer to Muon for experimentation? What is the performance difference between Muon and Adam after scaling up the model? Next, we will share our thought process.

Optimization Principle

#

Regarding optimizers, I previously made a brief comment in 《Appreciation of Muon Optimizer: An Essential Leap from Vectors to Matrices》 that most optimizer improvements are merely small patches, not entirely without value, but ultimately failing to give a profound and striking impression.

We need to start from a more fundamental principle to consider what constitutes a good optimizer. Intuitively, an ideal optimizer should have two characteristics: stability and speed. Specifically, each step’s update in an ideal optimizer should satisfy two points: 1. Minimize perturbation to the model; 2. Maximize contribution to the reduction of Loss. More directly, we don’t want to drastically change the model (stability), but we want to significantly reduce the Loss (speed), a typical “have your cake and eat it too” scenario.

How can these two characteristics be translated into mathematical language? Stability can be understood as a constraint on the update amount, while speed can be understood as finding the update amount that causes the fastest decrease in the loss function. Thus, this can be transformed into a constrained optimization problem. Using the notation from the previous text, for a matrix parameter $\boldsymbol{W}\in\mathbb{R}^{n\times m}$ with gradient $\boldsymbol{G}\in\mathbb{R}^{n\times m}$, when the parameter changes from $\boldsymbol{W}$ to $\boldsymbol{W}+\Delta\boldsymbol{W}$, the change in the loss function is

Then, finding the fast update amount under the premise of stability can be expressed as

Here, $\rho(\Delta\boldsymbol{W})\geq 0$ is a certain metric for stability, where a smaller value indicates greater stability, and $\eta$ is a constant less than 1, representing our requirement for stability. We will later see that it is actually the learning rate of the optimizer. If readers don’t mind, we can borrow a concept from theoretical physics and call the above principle the optimizer’s “Least Action Principle”.

Matrix Norms

#

The only uncertainty in the previous equation is the measure of stability $\rho(\Delta\boldsymbol{W})$. Once $\rho(\Delta\boldsymbol{W})$ is chosen, $\Delta\boldsymbol{W}$ can be explicitly solved (at least theoretically). To some extent, we can consider the fundamental difference between different optimizers to be their distinct definitions of stability.

Many readers, when first learning SGD, must have encountered statements like “the direction opposite to the gradient is the direction of the fastest local descent of the function value.” In the framework presented here, this statement implicitly chooses the matrix’s Frobenius norm $\Vert\Delta\boldsymbol{W}\Vert_F$ as the measure of stability. This means that the “direction of fastest descent” is not immutable; it can only be determined after selecting a specific measure. Changing the norm might result in a direction that is no longer opposite to the gradient.

The next natural question is: which norm can most appropriately measure stability? If we impose a strong constraint, it will be stable, but the optimizer will struggle, converging only to a suboptimal solution; conversely, if we weaken the constraint, the optimizer will run wild, leading to an extremely uncontrolled training process. Therefore, the ideal scenario is to find the most precise metric for stability. Considering that neural networks primarily involve matrix multiplications, let’s take $\boldsymbol{y}=\boldsymbol{x}\boldsymbol{W}$ as an example. We have

The meaning of the above equation is that when the parameter changes from $\boldsymbol{W}$ to $\boldsymbol{W}+\Delta\boldsymbol{W}$, the change in model output is $\Delta\boldsymbol{y}$. We hope that the magnitude of this change can be controlled by $\Vert\boldsymbol{x}\Vert$ and a function $\rho(\Delta\boldsymbol{W})$ related to $\Delta\boldsymbol{W}$. We then use this function as the metric for stability. From linear algebra, we know that the most accurate value for $\rho(\Delta\boldsymbol{W})$ is the spectral norm of $\Delta\boldsymbol{W}$, $\Vert\Delta\boldsymbol{W}\Vert_2$. Substituting this into the aforementioned equation yields

The solution to this optimization problem is Muon with $\beta=0$:

When $\beta > 0$, $\boldsymbol{G}$ is replaced by momentum $\boldsymbol{M}$, where $\boldsymbol{M}$ can be seen as a smoother estimate of the gradient. Therefore, it can still be understood as the conclusion of the above equation. Thus, we can state that “Muon is the fastest descent under the spectral norm.” As for Newton-Schulz iteration and similar methods, they are computational approximations and will not be elaborated on here. The detailed derivation has already been provided in 《Appreciation of Muon Optimizer: An Essential Leap from Vectors to Matrices》 and will not be repeated.

Weight Decay

#

At this point, we can answer the first question: Why choose to try Muon? Because, like SGD, Muon also provides the direction of fastest descent, but its spectral norm constraint is more precise than SGD’s Frobenius norm, thus offering greater potential. On the other hand, improving optimizers from the perspective of “choosing the most appropriate constraint for different parameters” seems more fundamental than various patch-like modifications.

Of course, potential does not equate to strength, and verifying Muon on larger models presents some “traps.” The first issue to emerge was the Weight Decay problem. Although we included Weight Decay when introducing Muon in 《Appreciation of Muon Optimizer: An Essential Leap from Vectors to Matrices》, it was actually not present in the original Muon proposal. When we initially implemented it according to the official version, we found that Muon converged quickly in the early stages, but was soon caught up by Adam, and various “internal issues” showed signs of collapse.

We quickly realized this might be a Weight Decay issue, so we added Weight Decay:

Continuing the experiments, as expected, Muon consistently maintained a lead over Adam, as shown in Figure 2 of the paper:

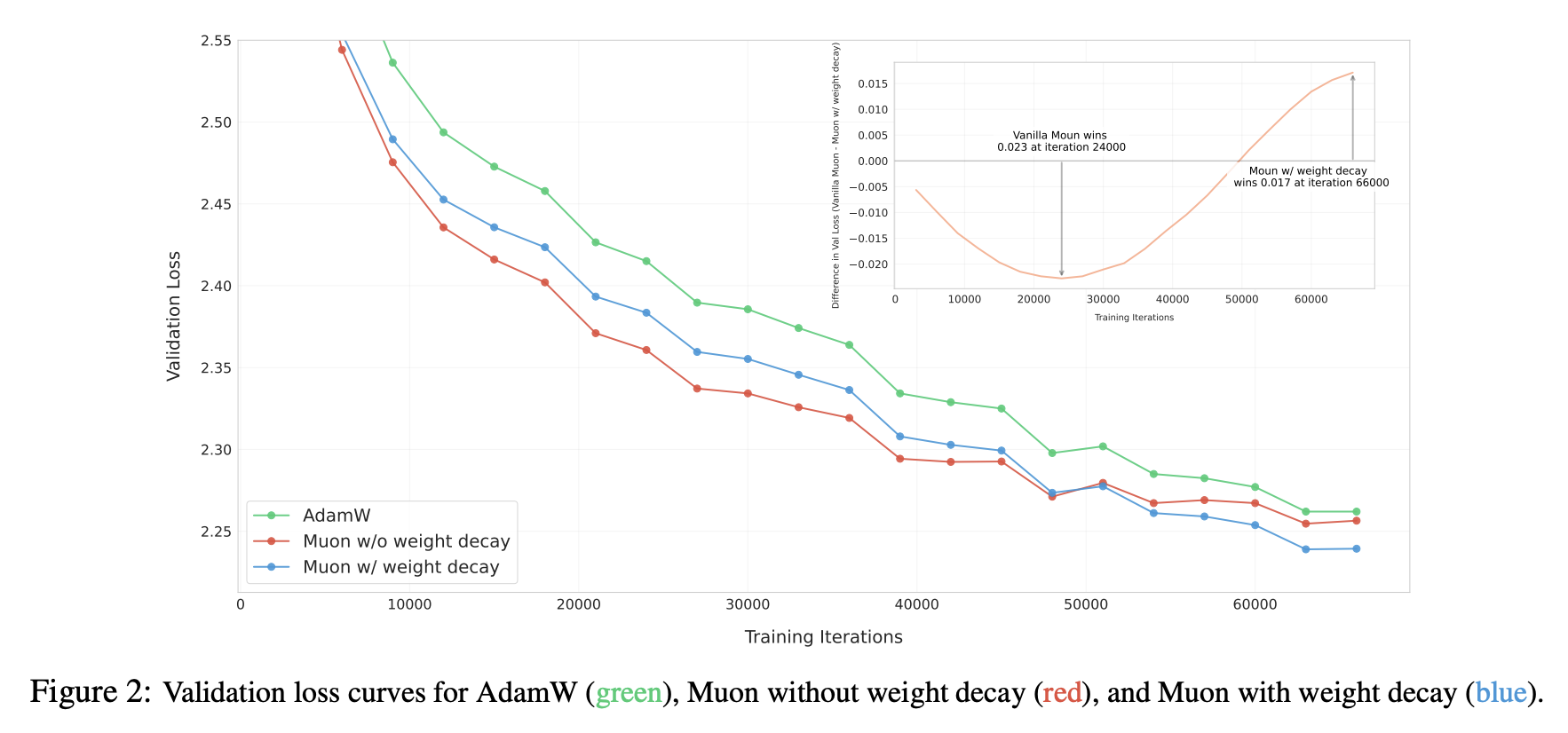
What role does Weight Decay play? From post-hoc analysis, a crucial aspect seems to be its ability to keep the parameter norms bounded:

Here, $\Vert\cdot\Vert$ denotes any matrix norm, meaning the above inequality holds for any matrix norm. $\boldsymbol{O}_t$ is the update vector provided by the optimizer, which for Muon is $\text{msign}(\boldsymbol{M})$. When we take the spectral norm, we have $\Vert\text{msign}(\boldsymbol{M})\Vert_2 = 1$, so for Muon, we have

This ensures the “health” of the model’s internals, because $\Vert\boldsymbol{x}\boldsymbol{W}\Vert\leq \Vert\boldsymbol{x}\Vert\Vert\boldsymbol{W}\Vert_2$. When $\Vert\boldsymbol{W}\Vert_2$ is controlled, it means $\Vert\boldsymbol{x}\boldsymbol{W}\Vert$ is also controlled, thus eliminating the risk of explosion, which is particularly important for issues like Attention Logits explosion. Of course, this upper bound is quite loose in most cases; in practice, the spectral norm of parameters is often significantly smaller than this bound. This inequality merely demonstrates that Weight Decay possesses the property of controlling norms.

RMS Alignment

#

When we decide to try a new optimizer, a vexing problem is how to quickly find nearly optimal hyperparameters. For instance, Muon has at least two hyperparameters: learning rate $\eta_t$ and decay rate $\lambda$. Grid search is certainly possible but time-consuming and laborious. Here, we propose a hyperparameter transfer strategy based on Update RMS alignment, which allows Adam’s well-tuned hyperparameters to be used for other optimizers.

First, for a matrix $\boldsymbol{W}\in\mathbb{R}^{n\times m}$, its RMS (Root Mean Square) is defined as

Simply put, RMS measures the average magnitude of each element in the matrix. We observed that the RMS of Adam’s updates is relatively stable, typically between 0.2 and 0.4, which is why theoretical analyses often use SignSGD as an approximation for Adam. Based on this, we suggest aligning the Update RMS of the new optimizer to 0.2 via RMS Normalization:

In this way, we can reuse Adam’s $\eta_t$ and $\lambda$ to achieve roughly the same magnitude of parameter updates at each step. Practice shows that migrating from Adam to Muon using this simple strategy can yield significantly better results than Adam, approaching those obtained by further fine-grained hyperparameter search for Muon. Notably, Muon’s $\text{RMS}(\boldsymbol{O}_t)=\text{RMS}(\boldsymbol{U}_{[:,:r]}\boldsymbol{V}_{[:,:r]}^{\top})$ can also be calculated analytically:

That is, $\text{RMS}(\boldsymbol{O}_t) = \sqrt{r/nm}$. In practice, the probability of a matrix being strictly low-rank is relatively small, so $r$ can be considered equal to $\min(n,m)$, thus yielding $\text{RMS}(\boldsymbol{O}_t) = \sqrt{1/\max(n,m)}$. Therefore, we ultimately did not use RMS Norm but rather its equivalent analytical version:

This final equation indicates that it is not suitable for all parameters to use the same learning rate in Muon. For example, Moonlight is an MoE model with many matrix parameters whose shapes deviate significantly from square matrices, leading to a large span in $\max(n,m)$. If a single learning rate is used, it will inevitably cause synchronization issues where some parameters learn too fast/slow, thereby affecting the final performance.

Experimental Analysis

#

We conducted a fairly comprehensive comparison between Adam and Muon on an MoE model of size 2.4B/16B, finding that Muon showed clear advantages in both convergence speed and final performance. For detailed comparison results, we recommend referring to the original paper; only a portion is shared here.

Github: https://github.com/MoonshotAI/Moonlight

First, a relatively objective comparison table, including our own controlled variable training comparisons of Muon and Adam, as well as comparisons with external models (DeepSeek) trained with Adam using the same architecture (for easy comparison, Moonlight’s architecture is identical to DSV3-Small), demonstrating Muon’s unique advantages:

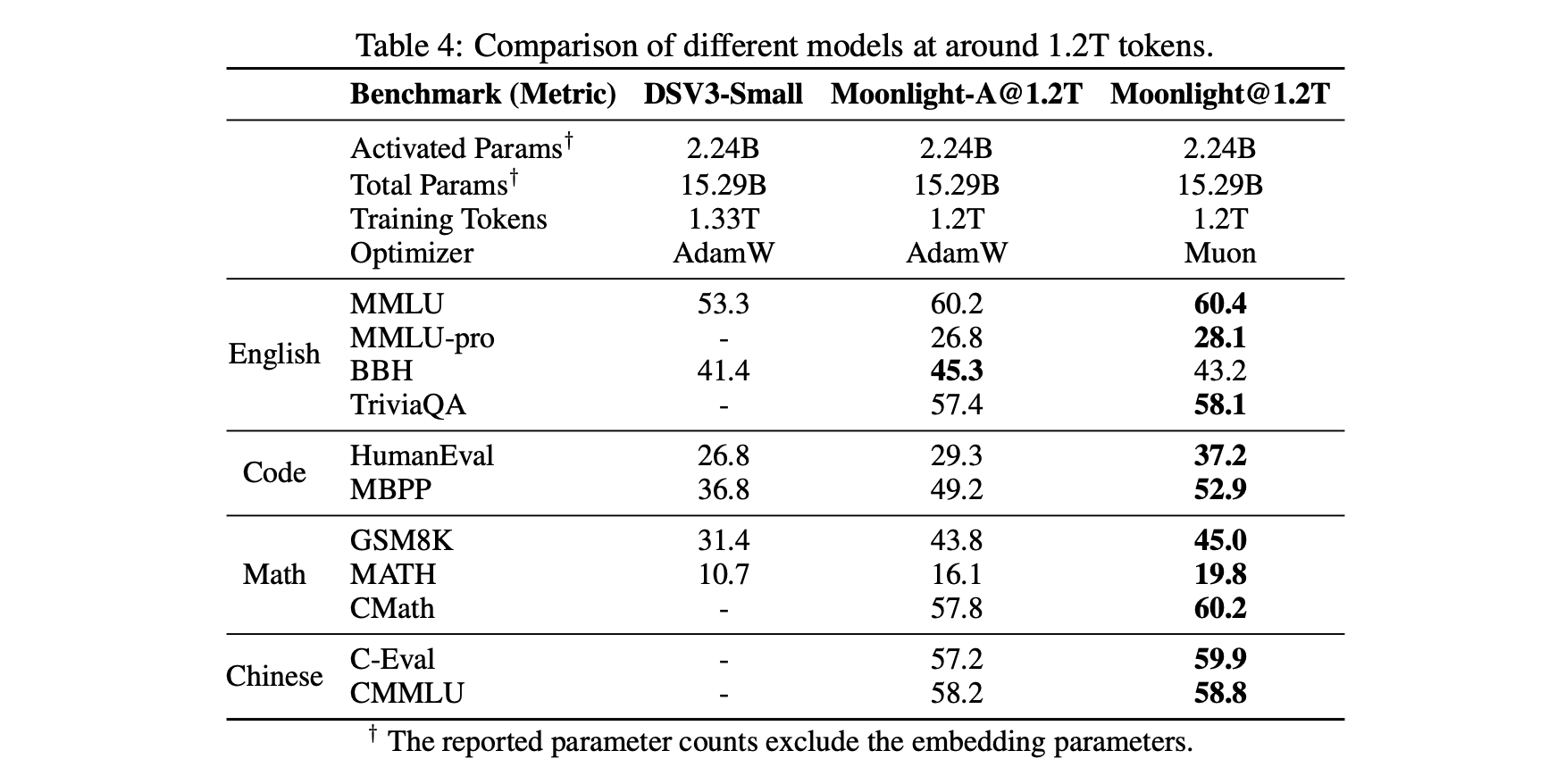
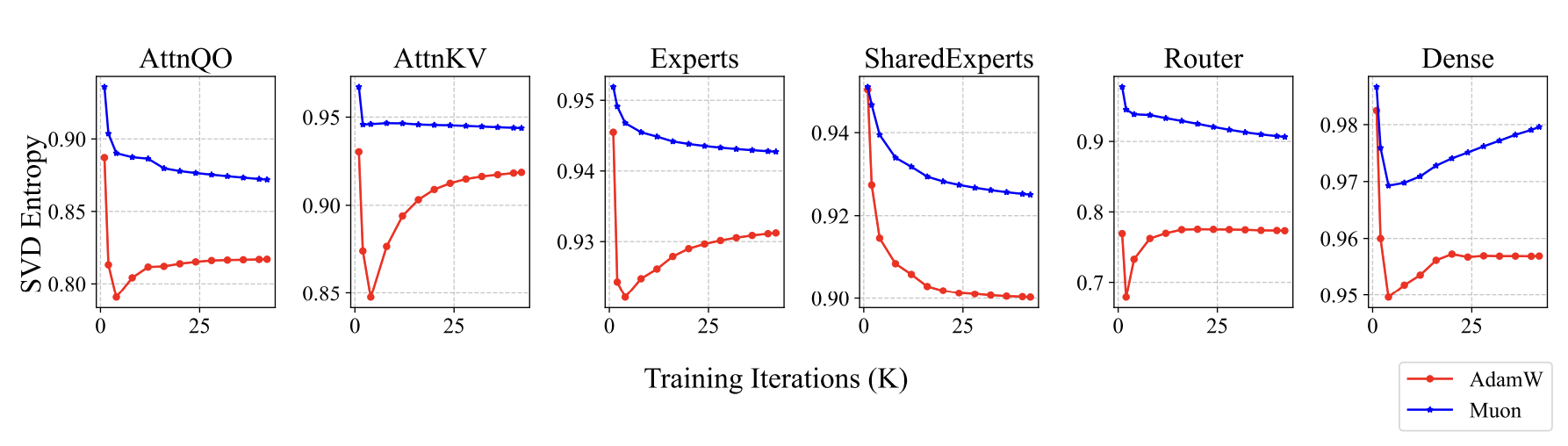
What’s different about the models trained with Muon? Since we previously stated that Muon represents the fastest descent under the spectral norm, and the spectral norm is the largest singular value, we thought of monitoring and analyzing singular values. Indeed, we found some interesting signals: the parameters trained by Muon exhibited a relatively more uniform distribution of singular values. We use singular value entropy to quantitatively describe this phenomenon:

Here, $\boldsymbol{\sigma}=(\sigma_1,\sigma_2,\cdots,\sigma_n)$ represents all singular values of a certain parameter. Parameters trained with Muon have higher entropy, meaning their singular values are more uniformly distributed. This implies that the parameter is less compressible, suggesting that Muon more fully leverages the potential of the parameters:

Another interesting finding is that when we use Muon for fine-tuning (SFT), we might obtain suboptimal solutions if Muon was not used for pre-training. Specifically, if both pre-training and fine-tuning use Muon, the performance is best. However, for the other three combinations (Adam+Muon, Muon+Adam, Adam+Adam), there was no clear pattern in the superiority or inferiority of their effects.

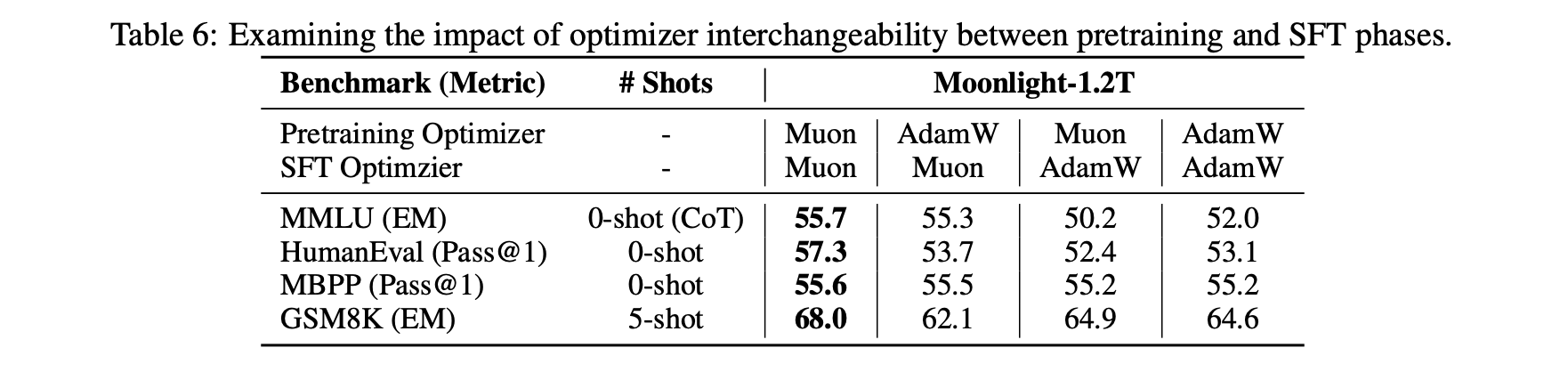
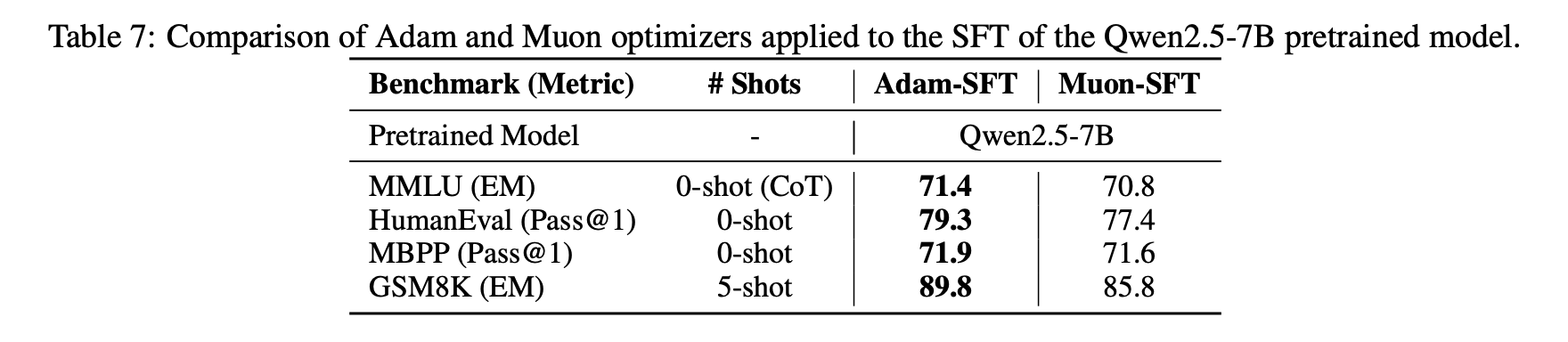
This phenomenon suggests that certain specific initializations might be detrimental to Muon. Conversely, it’s also possible that some initializations are more beneficial to Muon. We are still exploring the underlying principles.

Further Thoughts

#

Overall, in our experiments, Muon’s performance appeared very competitive compared to Adam. As a new optimizer with significant formal differences from Adam, Muon’s performance is not merely “remarkable,” but also indicates that it might have captured some fundamental characteristics.

Previously, a viewpoint circulated within the community: Adam performs well because mainstream model architecture improvements are “overfitting” to Adam. This idea likely originated from 《Neural Networks (Maybe) Evolved to Make Adam The Best Optimizer》. It might seem somewhat absurd, but it is actually profound. Consider this: when we try to improve a model, we train it with Adam to observe its performance. If the performance is good, we keep it; otherwise, we discard it. But is this good performance due to the model being inherently better, or simply because it aligns better with Adam?

This becomes quite intriguing. While not all work, certainly at least a portion of it achieves better results because it is more compatible with Adam. Thus, over time, model architectures tend to evolve in a direction that favors Adam. In this context, an optimizer significantly different from Adam still managing to “break out” is particularly worthy of attention and thought. Note that neither I nor my affiliated company are the originators of Muon, so these remarks are purely “from the heart” and not intended as self-promotion.

What more work can be done with Muon next? In fact, quite a lot. For instance, the aforementioned issue of suboptimal “Adam pre-training + Muon fine-tuning” still warrants further necessary and valuable analysis, as most open-source model weights today are trained with Adam. If Muon fine-tuning doesn’t work well, it will inevitably affect its widespread adoption. Of course, we can also use this opportunity to deepen our understanding of Muon (learning from bugs).

Another extended thought is that Muon is based on the spectral norm, which is the largest singular value. In fact, we can also construct a series of norms based on singular values, such as Schatten norms. Extending Muon to these more generalized norms and then tuning parameters theoretically presents an opportunity for even better results. Furthermore, after Moonlight was released, some readers asked how to design µP (maximal update parametrization) under Muon, which is also a problem that needs to be solved.

Summary (formatted)

#

This article describes our large-scale practice with the Muon optimizer (Moonlight) and shares our latest thoughts on it.

@online{kexuefm-10739,
        title={Muon Sequel: Why Did We Choose to Try Muon?},
        author={苏剑林},
        year={2025},
        month={02},
        url={\url{https://kexue.fm/archives/10739}},
}