Simpler Yet More Profound Spectral Condition Scaling

By Su Jianlin | 2025-03-24 | 25346 Readers

In the article "A Preliminary Exploration of muP: Scaling Laws for Hyperparameters Across Model Scales", we derived muP (Maximal Update Parametrization) based on the scale invariance of forward propagation, backpropagation, loss increment, and feature changes. For some readers, this process might still seem a bit cumbersome, but it is actually a significant simplification compared to the original paper. It’s worth noting that we introduced muP relatively comprehensively within a single article, whereas the muP paper is actually the 5th paper in the author’s Tensor Programs series!

However, the good news is that in a subsequent study, "A Spectral Condition for Feature Learning", the author discovered a new way of understanding (hereinafter referred to as "spectral condition"), which is more intuitive and concise than both the original muP derivation and my derivation. Yet, it yields richer results than muP, making it a higher-order version of muP, a representative work that is both simple and profound.

Preparation

#

As the name suggests, the spectral condition is related to the spectral norm. Its starting point is a basic inequality of the spectral norm:

where $\boldsymbol{x}\in\mathbb{R}^{d_{in}}, \boldsymbol{W}\in\mathbb{R}^{d_{in}\times d_{out}}$. As for $\Vert\cdot\Vert_2$, we can call it the "$2$-norm." For $\boldsymbol{x},\boldsymbol{x}\boldsymbol{W}$, they are both vectors, and the $2$-norm is their vector magnitude; $\boldsymbol{W}$ is a matrix, and its $2$-norm is also called the spectral norm, which equals the smallest constant $C$ such that $\Vert\boldsymbol{x}\boldsymbol{W}\Vert_2\leq C\Vert\boldsymbol{x}\Vert_2$ always holds. In other words, the above inequality is actually a direct consequence of the definition of the spectral norm, so no additional proof is needed.

Regarding the spectral norm, you can also refer to blog posts like "Lipschitz Constraints in Deep Learning: Generalization and Generative Models" and "The Road to Low-Rank Approximation (II): SVD"; we won’t elaborate here. There is also a simpler $F$-norm for matrices, which is a straightforward generalization of the vector norm:

From the perspective of singular values, the spectral norm equals the largest singular value of a matrix, while the $F$-norm equals the square root of the sum of squares of all singular values of the matrix. Therefore, it always holds that

This inequality describes the equivalence between the spectral norm and the $F$-norm (here, equivalence means an inequality relationship, not complete equality). So, when we encounter problems that are difficult to analyze due to the complexity of the spectral norm, we can consider replacing it with the $F$-norm to obtain an approximate result.

Finally, let’s define RMS (Root Mean Square), which is a variant of the vector norm:

If we generalize to matrices, it would be $\Vert\boldsymbol{W}\Vert_{RMS} = \Vert \boldsymbol{W}\Vert_F/\sqrt{d_{in} d_{out}}$. In fact, from the name itself, it’s easy to understand: the vector norm or matrix $F$-norm can be called "Root Sum Square," while RMS replaces "Sum" with "Mean." It is mainly used as an average scale indicator for vector or matrix elements. Now, substituting RMS into inequality $\text{neq:spec-2}$, we can obtain

Expected Properties

#

Our previous approach to deriving muP involved carefully analyzing the forms of forward propagation, backpropagation, loss increment, and feature changes, and then adjusting initialization and learning rates to achieve their scale invariance. After ‘purifying’ these conditions, the spectral condition found that only forward propagation and feature changes are sufficient.

Simply put, the spectral condition expects both the output and the increment of each layer to possess scale invariance. How should this statement be understood? If we denote each layer as $\boldsymbol{x}_k= f(\boldsymbol{x}_{k-1}; \boldsymbol{W}_k)$ for example, this statement can be translated as "expecting both $\Vert\boldsymbol{x}_k\Vert_{RMS}$ and $\Vert\Delta\boldsymbol{x}_k\Vert_{RMS}$ to be $\mathcal{O}(1)$":

1. $\Vert\boldsymbol{x}_k\Vert_{RMS}=\mathcal{O}(1)$ is easy to understand; it represents the stability of forward propagation, a requirement also present in the previous article’s derivation;
2. $\Delta\boldsymbol{x}_k$ denotes the change in $\boldsymbol{x}_k$ caused by parameter changes, so $\Vert\Delta\boldsymbol{x}_k\Vert_{RMS}=\mathcal{O}(1)$ combines the requirements for backpropagation and feature changes.

Readers might wonder: shouldn’t there be at least a "loss increment" requirement? Not necessarily. In fact, we can prove that if $\Vert\boldsymbol{x}_k\Vert_{RMS}$ and $\Vert\Delta\boldsymbol{x}_k\Vert_{RMS}$ are both $\mathcal{O}(1)$ for every layer, then $\Delta\mathcal{L}$ will automatically be $\mathcal{O}(1)$. This is the first beautiful aspect of the spectral condition idea: it reduces the four conditions originally needed to derive muP to just two, simplifying the analysis steps.

The proof is not difficult. The key here is that we assume $\Vert\boldsymbol{x}_k\Vert_{RMS}=\mathcal{O}(1)$ and $\Vert\Delta\boldsymbol{x}_k\Vert_{RMS}=\mathcal{O}(1)$ hold for every layer, so it naturally holds for the last layer as well. Assuming the model has $K$ layers in total, and the loss function for a single sample is $\ell$, then it is a function of $\boldsymbol{x}_K$, i.e., $\ell(\boldsymbol{x}_K)$. For simplicity, the label input is omitted here, as it is not a variable for the following analysis.

According to the assumption, $\Vert\boldsymbol{x}_K\Vert_{RMS}$ is $\mathcal{O}(1)$, so $\ell(\boldsymbol{x}_K)$ is naturally $\mathcal{O}(1)$; furthermore, because $\Vert\Delta\boldsymbol{x}_K\Vert_{RMS}$ is $\mathcal{O}(1)$, it follows that $\Vert\boldsymbol{x}_K + \Delta\boldsymbol{x}_K\Vert_{RMS}\leq \Vert\boldsymbol{x}_K\Vert_{RMS} + \Vert\Delta\boldsymbol{x}_K\Vert_{RMS}$ is also $\mathcal{O}(1)$, and thus $\ell(\boldsymbol{x}_K + \Delta\boldsymbol{x}_K)$ is $\mathcal{O}(1)$, so

Therefore, the loss increment $\Delta \ell$ for a single sample is $\mathcal{O}(1)$, and $\Delta\mathcal{L}$ is the average of all $\Delta \ell$, so it is also $\mathcal{O}(1)$. This proves that $\Vert\boldsymbol{x}_k\Vert_{RMS}=\mathcal{O}(1)$ and $\Vert\Delta\boldsymbol{x}_k\Vert_{RMS}=\mathcal{O}(1)$ automatically encompass $\Delta\mathcal{L}=\mathcal{O}(1)$. In essence, $\Delta\mathcal{L}$ is a function of the last layer’s output and its increment, and if they are both stable, $\Delta\mathcal{L}$ naturally becomes stable.

Spectral Condition

#

Next, let’s see how to establish the two expected properties. Since neural networks primarily involve matrix multiplication, we first consider the simplest linear layer $\boldsymbol{x}_k = \boldsymbol{x}_{k-1} \boldsymbol{W}_k$, where $\boldsymbol{W}_k\in\mathbb{R}^{d_{k-1}\times d_k}$. To satisfy the condition $\Vert\boldsymbol{x}_k\Vert_{RMS}=\mathcal{O}(1)$, the spectral condition does not assume independent and identical distribution and then calculate expected variance as in traditional initialization analysis; instead, it directly applies inequality $\text{neq:spec-rms}$:

Note that this inequality can achieve equality and is, in some sense, the most precise. Therefore, if the input $\Vert\boldsymbol{x}_{k-1}\Vert_{RMS}$ is already $\mathcal{O}(1)$, then to make the output $\Vert\boldsymbol{x}_k\Vert_{RMS}=\mathcal{O}(1)$, we need to have

This introduces the first spectral condition—the requirement on the spectral norm of $\boldsymbol{W}_k$. It is independent of initialization and distribution assumptions, being purely a result of analysis and algebra. This is what I consider the second beautiful aspect of the spectral condition—it simplifies the analysis process. Of course, this omits the basic content of spectral norms; if added, the total length might not be shorter than analysis under distribution assumptions, but distribution assumptions ultimately appear more limited than the flexible algebraic framework here.

After analyzing $\Vert\boldsymbol{x}_k\Vert_{RMS}$, it’s time for $\Vert\Delta\boldsymbol{x}_k\Vert_{RMS}$. The increment $\Delta\boldsymbol{x}_k$ originates from two parts: first, the parameters change from $\boldsymbol{W}_k$ to $\boldsymbol{W}_k+\Delta \boldsymbol{W}_k$; second, the input $\boldsymbol{x}_{k-1}$ changes from $\boldsymbol{x}_{k-1}$ to $\boldsymbol{x}_{k-1} + \Delta\boldsymbol{x}_{k-1}$ due to parameter changes. Therefore,

Hence

Let’s analyze term by term

It is thus clear that for $\Vert\Delta\boldsymbol{x}_k\Vert_{RMS}=\mathcal{O}(1)$, we need

This is the second spectral condition—the requirement on the spectral norm of $\Delta\boldsymbol{W}_k$.

The above analysis did not consider non-linearity. In fact, as long as the activation function is element-wise and its derivative can be bounded by some constant (common activation functions like ReLU, Sigmoid, Tanh all satisfy this), then the result remains consistent even when considering non-linear activation functions. This is what the previous article’s analysis referred to as "the influence of activation functions being scale-independent." If readers are still unsure, they can derive it themselves.

Spectral Normalization

#

Now that we have the two spectral conditions $\text{eq:spec-c1}$ and $\text{eq:spec-c2}$, the next step is to figure out how to design the model itself and its optimization to satisfy these two conditions.

Note that both $\boldsymbol{W}_k$ and $\Delta \boldsymbol{W}_k$ are matrices. The standard method for a matrix to satisfy spectral norm conditions is typically Spectral Normalization (SN), and this case is no exception. First, we need to ensure that the initialized $\boldsymbol{W}_k$ satisfies $\Vert\boldsymbol{W}_k\Vert_2=\mathcal{O}\left(\sqrt{\frac{d_k}{d_{k-1}}}\right)$. This can be achieved by selecting an arbitrary initialization matrix $\boldsymbol{W}_k'$, and then performing spectral normalization:

Here, $\sigma > 0$ is a scale-independent constant; similarly, for any update amount $\boldsymbol{U}_k$ given by an optimizer, we can reconstruct $\Delta \boldsymbol{W}_k$ through spectral normalization:

where $\eta > 0$ is also a scale-independent constant (learning rate). In this way, every step will have $\Vert\Delta\boldsymbol{W}_k\Vert_2=\mathcal{O}\left(\sqrt{\frac{d_k}{d_{k-1}}}\right)$. Since the spectral norm of both the initialization and each update step satisfies $\mathcal{O}\left(\sqrt{\frac{d_k}{d_{k-1}}}\right)$, $\Vert\boldsymbol{W}_k\Vert_2$ will satisfy $\mathcal{O}\left(\sqrt{\frac{d_k}{d_{k-1}}}\right)$ throughout, thus fulfilling both spectral conditions.

At this point, readers might wonder if considering only the stability of initialization and increments can truly guarantee the stability of $\boldsymbol{W}_k$. Is it not possible for $\Vert\boldsymbol{W}_k\Vert_{RMS}\to\infty$? The answer is that it is possible. The $\mathcal{O}\left(\sqrt{\frac{d_k}{d_{k-1}}}\right)$ here emphasizes the relationship with model scale (currently mainly width). It does not rule out the possibility of training collapse due to improper settings of other hyperparameters. What it means to convey is that after setting it this way, even if a collapse occurs, the reason is unrelated to scale changes.

Singular Value Clipping

#

To satisfy the spectral norm condition, besides the standard method of spectral normalization, we can also consider Singular Value Clipping (hereinafter referred to as "SVC"). This part is an addition by the author and did not appear in the original paper, but it can explain some interesting results.

From the perspective of singular values, spectral normalization scales the largest singular value to 1 and synchronously scales the remaining singular values. Singular value clipping, from a certain angle, is more lenient: it only sets singular values greater than 1 to 1, but does not change singular values that are already less than or equal to 1:

In contrast, spectral normalization is $\mathop{\text{SN}}(\boldsymbol{W})=\boldsymbol{U}(\boldsymbol{\Lambda}/\max(\boldsymbol{\Lambda}))\boldsymbol{V}^{\top}$. Replacing spectral normalization with singular value clipping, we obtain

The disadvantage of singular value clipping is that it can only guarantee the clipped spectral norm equals 1 if at least one singular value is greater than or equal to 1. If not, we could consider multiplying by a $\lambda > 0$ and then clipping, i.e., changing it to $\mathop{\text{SVC}}(\lambda\boldsymbol{W})$. However, different scaling factors would yield different results, and it’s hard for us to determine a suitable scaling factor. Nevertheless, we can consider a limiting version

Here, $\mathop{\text{msign}}$ is the matrix-version sign function from Muon (refer to "Appreciation of Muon Optimizer: An Essential Leap from Vectors to Matrices"). Using $\mathop{\text{msign}}$ to replace spectral normalization or singular value clipping, we obtain

In this way, we effectively obtain a generalized Muon optimizer. The standard Muon applies $\mathop{\text{msign}}$ to the momentum, while this allows us to apply $\mathop{\text{msign}}$ to the update amount from any existing optimizer. Coincidentally, someone on Twitter recently performed an experiment applying $\mathop{\text{msign}}$ to Adam’s update amount (which they called "Mudamw," link), and found that its performance was slightly better than Muon, as shown in the figure below:

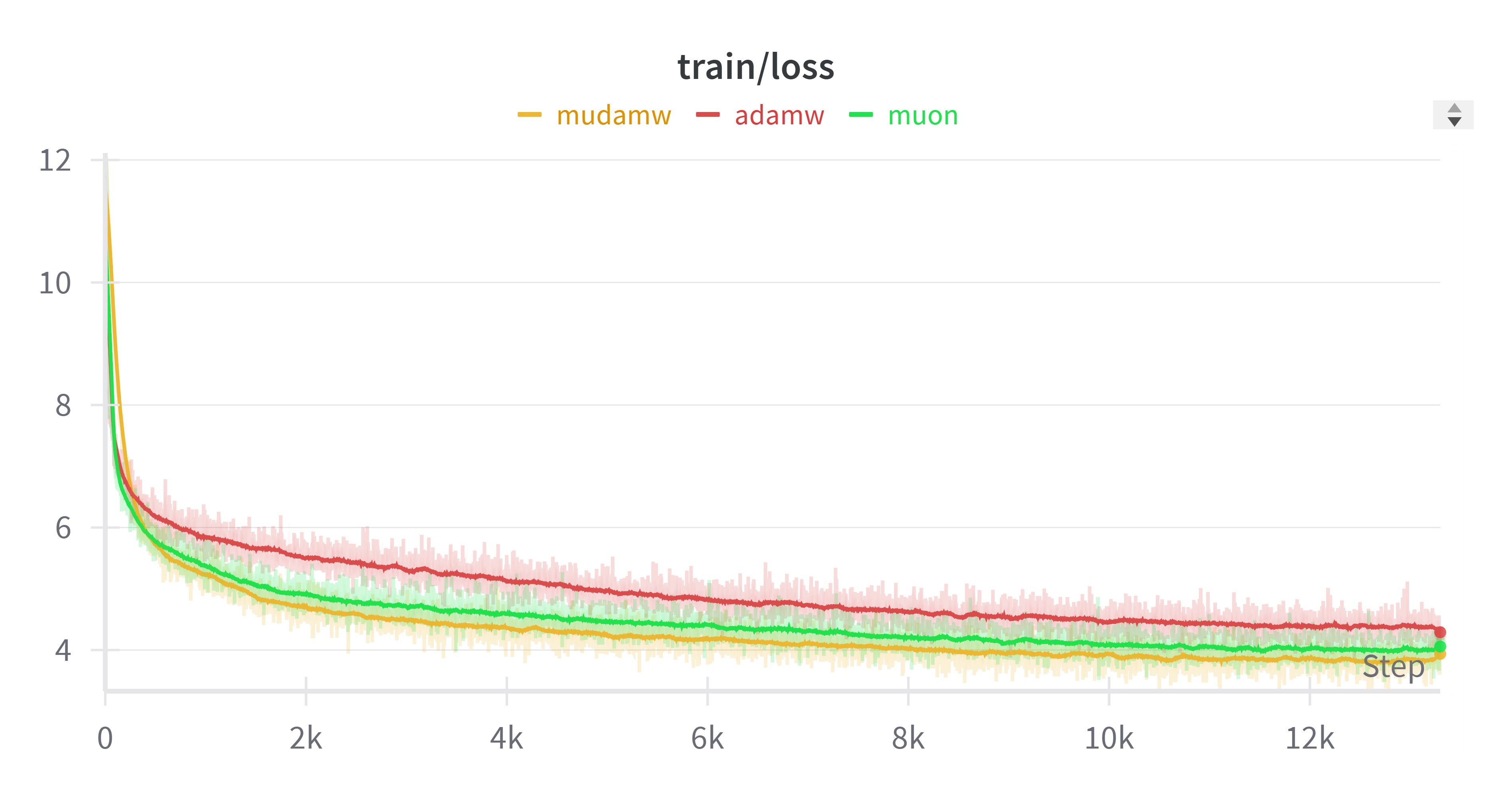
After seeing this, we tried it on small models and surprisingly found similar conclusions! So, it’s possible that applying $\mathop{\text{msign}}$ to existing optimizers might yield better results. The feasibility of this operation is difficult to explain under the original Muon framework, but here, if we understand it as singular value clipping (a limiting version) applied to the update amount, this result naturally follows.

Approximate Estimation

#

It is generally believed that operations related to SVD (Singular Value Decomposition), such as spectral normalization, singular value clipping, or $\mathop{\text{msign}}$, are relatively expensive. Therefore, we still hope to find simpler forms.

(Note: In fact, our Moonlight work shows that if implemented well, even performing $\mathop{\text{msign}}$ at every update step incurs very limited additional cost. Therefore, the content of this section, for now, seems to be more about exploring explicit scaling laws rather than saving computational costs).

First is initialization. Initialization is a one-time process, so a slightly larger computational cost isn’t really an issue. Thus, the previous scheme of random initialization followed by spectral normalization/singular value clipping/$\mathop{\text{msign}}$ can still be retained. If one still seeks perfection, a statistical result can be utilized: for a $d_{k-1}\times d_k$ matrix sampled independently and repeatedly from a standard normal distribution, its largest singular value is approximately $\sqrt{d_{k-1}} + \sqrt{d_k}$. This means that if the sampling standard deviation is changed to

this can satisfy the requirement $\Vert\boldsymbol{W}_k\Vert_2=\mathcal{O}\left(\sqrt{\frac{d_k}{d_{k-1}}}\right)$ during the initialization phase. For the proof of this statistical result, you can refer to resources like "High-Dimensional Probability" and "Marchenko-Pastur law"; we won’t elaborate here.

Next, let’s examine the update amount. It’s relatively more troublesome because the spectral norm of an arbitrary update amount $\boldsymbol{U}_k$ is not easily estimated. Here, we need to utilize an empirical conclusion: that the gradients of parameters and the update amounts are typically low-rank. Here, ’low-rank’ doesn’t necessarily mean strictly low-rank in a mathematical sense, but rather that the largest few (whose number is independent of the model scale) singular values significantly exceed the remaining singular values, making low-rank approximation applicable. This is also the theoretical basis for various LoRA optimizations.

A direct corollary of this empirical assumption is the approximate similarity between the spectral norm and the $F$-norm. Since the spectral norm is the largest singular value, and under the aforementioned assumption, the $F$-norm is approximately equal to the square root of the sum of squares of the largest few singular values, then the two are consistent at least in terms of scale, i.e., $\mathcal{O}(\Vert\boldsymbol{U}_k\Vert_2)=\mathcal{O}(\Vert\boldsymbol{U}_k\Vert_F)$. Next, we utilize the relationship between $\Delta\mathcal{L}$ and $\Delta\boldsymbol{W}_k$:

Here, $\langle\cdot,\cdot\rangle_F$ is the $F$-inner product, meaning the matrix flattened as a vector for inner product calculation, and the inequality is due to the Cauchy-Schwarz inequality. Based on the above equation, we have

Don’t forget that we have already proven that satisfying the two spectral conditions necessarily implies $\Delta\mathcal{L}=\mathcal{O}(1)$. Combining this with the above equation, we can obtain that when $\Vert\Delta\boldsymbol{W}_k\Vert_2=\mathcal{O}\left(\sqrt{\frac{d_k}{d_{k-1}}}\right)$, we have

This is an important estimation result regarding the magnitude of gradients. It is directly derived from the two spectral conditions, avoiding explicit gradient computation. This is the third beautiful aspect of the spectral condition: it allows us to obtain relevant estimates without needing to calculate gradient expressions via the chain rule.

Learning Rate Strategy

#

Applying estimation $\text{eq:grad-norm}$ to SGD, i.e., $\Delta \boldsymbol{W}_k = -\eta_k \nabla_{\boldsymbol{W}_k}\mathcal{L}$, according to equation $\text{eq:grad-norm}$, we have $\Vert\nabla_{\boldsymbol{W}_k}\mathcal{L}\Vert_2=\mathcal{O}\left(\sqrt{\frac{d_{k-1}}{d_k}}\right)$. To achieve the target $\Vert\Delta\boldsymbol{W}_k\Vert_2=\mathcal{O}\left(\sqrt{\frac{d_k}{d_{k-1}}}\right)$, we need to have

As for Adam, we still approximate $\Delta \boldsymbol{W}_k = -\eta_k \mathop{\text{sign}}(\nabla_{\boldsymbol{W}_k}\mathcal{L})$ with SignSGD. Since $\text{sign}$ is generally $\pm 1$, we have $\Vert\mathop{\text{sign}}(\nabla_{\boldsymbol{W}_k}\mathcal{L})\Vert_F = \mathcal{O}(\sqrt{d_{k-1} d_k})$. Therefore, to achieve the target $\Vert\Delta\boldsymbol{W}_k\Vert_2=\mathcal{O}\left(\sqrt{\frac{d_k}{d_{k-1}}}\right)$, we need to have

Now we can compare the results of the spectral condition with muP. muP assumes we want to build a model mapping $\mathbb{R}^{d_{in}}\mapsto\mathbb{R}^{d_{out}}$. It divides the model into three parts: first, a $d_{in}\times d$ matrix projects the input to $d$ dimensions; then, modeling is performed in the $d$-dimensional space, where parameters are $d\times d$ square matrices; finally, a $d\times d_{out}$ matrix produces the $d_{out}$-dimensional output. Correspondingly, muP’s conclusions are also divided into three parts: input, intermediate, and output.

Regarding initialization, muP’s input variance is $1/d_{in}$, output variance is $1/d^2$, and the variance of remaining parameters is $1/d$, whereas the spectral condition result is a single equation $\text{eq:spec-std}$. However, a close inspection reveals that equation $\text{eq:spec-std}$ already encompasses muP’s three cases: assuming the sizes of input, intermediate, and output matrices are $d_{in}\times d,d\times d,d\times d_{out}$, substituting into equation $\text{eq:spec-std}$ yields

Readers might wonder why only $d\to\infty$ is considered. This is because $d_{in}$ and $d_{out}$ are task-related numbers, effectively constants. The only variable model scale is $d$. muP studies the asymptotic rules of hyperparameters with respect to model scale, so it always refers to simplified rules when $d$ is sufficiently large.

Regarding learning rates, for SGD, muP’s input learning rate is $d$, output learning rate is $1/d$, and the learning rate for remaining parameters is $1$. Note that these relationships are proportional to, not equal to. The spectral condition’s result $\text{eq:sgd-eta}$ also covers these three cases. Similarly, for Adam, muP’s input learning rate is $1$, output learning rate is $1/d$, and the learning rate for remaining parameters is $1/d$. The spectral condition still describes these three cases with a single equation $\text{eq:adam-eta}$.

Therefore, the spectral condition obtains a simpler result in a way that (in my opinion) is more straightforward, and the practical implications of this simpler result are richer than muP, as its results do not make overly strong assumptions about model architecture or parameter shapes. For this reason, I refer to the spectral condition as a higher-order version of muP.

Summary (formatted)

#

This article introduced an upgraded version of muP—the spectral condition. It analyzes the conditions for stable model training by starting from inequalities related to spectral norms, yielding richer results than muP in a more convenient manner.

@online{kexuefm-10795,
        title={Higher-Order muP: Simpler Yet More Profound Spectral Condition Scaling},
        author={苏剑林},
        year={2025},
        month={03},
        url={\url{https://kexue.fm/archives/10795}},
}