Advancing Muon Further on its Scale-up Journey

By Su Jianlin | 2025-07-12 | 45728 Readers

Four months ago, we released Moonlight, validating the effectiveness of the Muon optimizer on a 16B MoE model. In Moonlight, we confirmed the necessity of adding Weight Decay to Muon and proposed a technique for migrating Adam hyperparameters by aligning Update RMS, which enabled Muon to be quickly applied to LLM training. However, when we attempted to extend Muon further to models with hundreds of billions of parameters, we encountered a new “roadblock”—MaxLogit explosion.

To address this problem, we proposed a simple yet extremely effective new method, which we call “QK-Clip.” This method approaches and solves the MaxLogit phenomenon from a fundamental perspective, without compromising model performance, and has become one of the key training techniques for our newly released trillion-parameter model, “Kimi K2.”

Problem Description

#

Let’s first briefly introduce the MaxLogit explosion phenomenon. Recalling the definition of Attention:

The scaling factor $1/\sqrt{d}$ is omitted here because it can always be absorbed into the definitions of $\boldsymbol{Q}$ and $\boldsymbol{K}$. The “Logit” in “MaxLogit explosion” refers to the Attention matrix before Softmax, i.e., $\boldsymbol{Q}\boldsymbol{K}^{\top}$, while MaxLogit refers to the maximum value among all Logits. We denote it as:

Here, $\max$ is actually also taken over the batch_size dimension, ultimately yielding a scalar. MaxLogit explosion means that $S_{\max}$ continuously increases as training progresses, with a growth rate that is linear or even superlinear, showing no signs of stabilization over a considerable period.

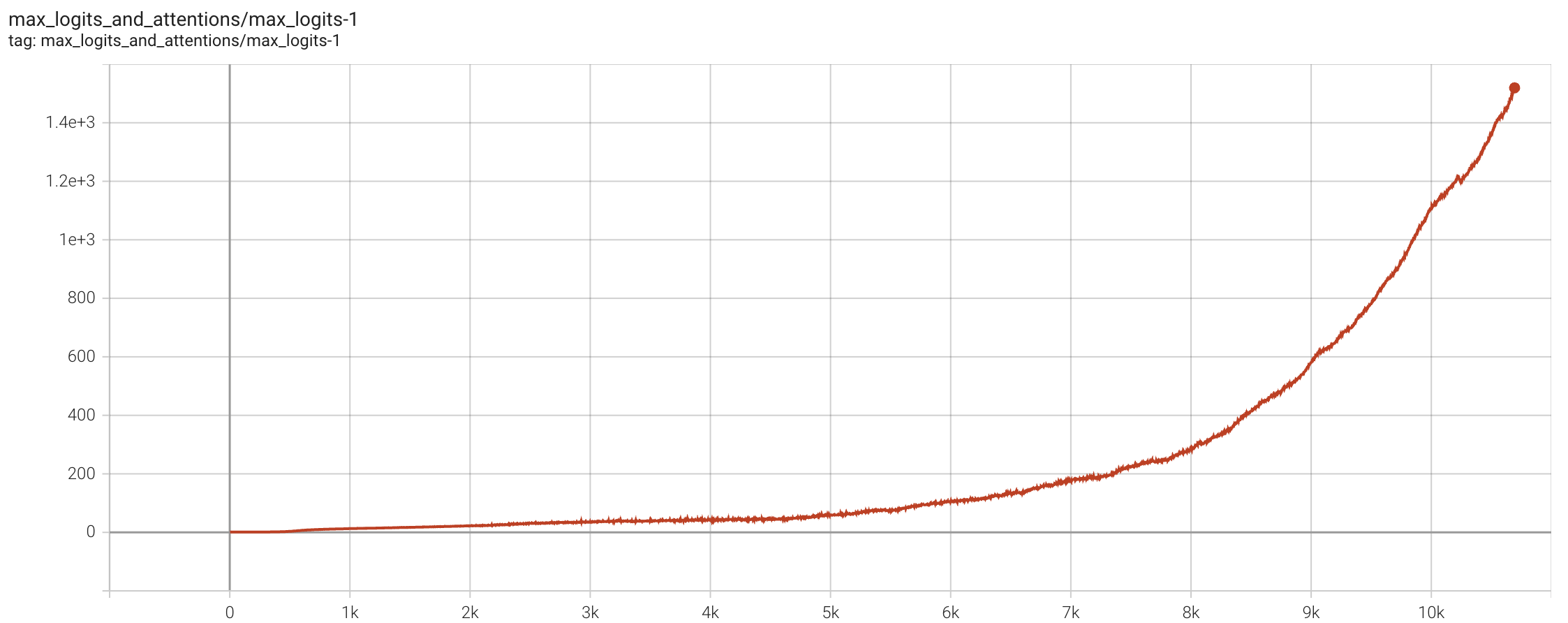
MaxLogit is essentially an outlier metric; its explosion means that outliers have exceeded the controllable range. Specifically, we have:

Since $\boldsymbol{x}$ typically undergoes RMSNorm, $\Vert\boldsymbol{x}_i\Vert \Vert\boldsymbol{x}_j\Vert$ generally does not explode. Therefore, MaxLogit explosion implies a risk of the spectral norms $\Vert\boldsymbol{W}_q\Vert,\Vert\boldsymbol{W}_k\Vert$ growing towards infinity, which is clearly not good news.

Since even very large values become less than 1 after Softmax, in fortunate cases, this phenomenon does not lead to severe consequences, at most wasting an Attention Head. However, in worse scenarios, it could cause Grad Spike or even training collapse. Therefore, for safety, MaxLogit explosion should be avoided as much as possible.

Existing Attempts

#

In “Muon Sequel: Why Did We Choose to Try Muon?”, we briefly analyzed that Weight Decay can prevent MaxLogit explosion to some extent. Therefore, the probability of MaxLogit explosion in small models is very low; even for a 16B model like Moonlight, MaxLogit would at most rise to 120 and then automatically decrease.

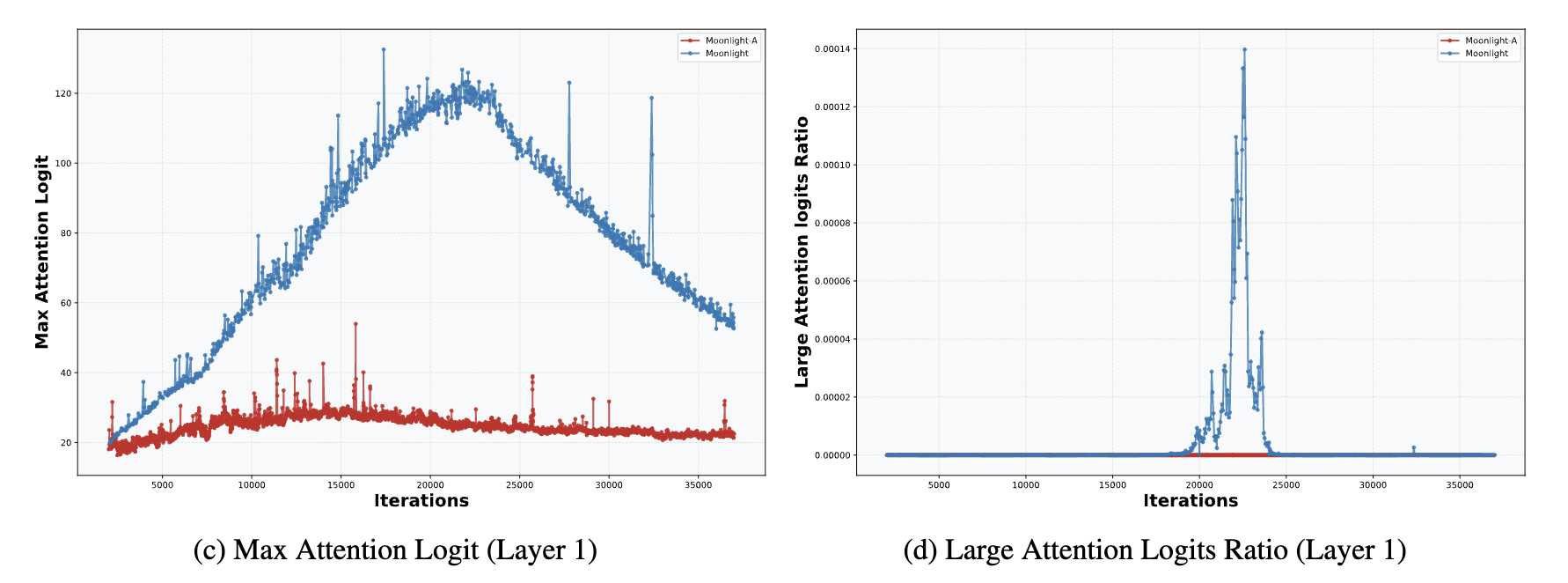
In other words, MaxLogit explosion occurs more frequently in models with very large numbers of parameters; the larger the model, the more unstable factors in training, and the harder it is for Weight Decay to stabilize training. Increasing Weight Decay at this point could naturally strengthen control, but it would also lead to significant performance degradation, making this approach unfeasible. Another relatively direct approach is to directly apply $\text{softcap}$ to the Logits:

Where $\text{softcap}(x;\tau) = \tau\tanh(x/\tau)$, introduced by Google’s Gemma2. Due to the boundedness of $\tanh$, $\text{softcap}$ naturally ensures that the Logits after $\text{softcap}$ are bounded, but it cannot guarantee that the Logits before $\text{softcap}$ are bounded (personally tested). Therefore, $\text{softcap}$ merely transforms one problem into another, without actually solving it.

Perhaps Google itself realized this, which is why in the later Gemma3, $\text{softcap}$ was no longer used, replaced by “QK-Norm”:

QK-Norm is indeed a very effective method for suppressing MaxLogit. However, it is only suitable for MHA, GQA, etc., and not for MLA, because QK-Norm requires $\boldsymbol{Q}$ and $\boldsymbol{K}$ to be materialized. For MLA, $\boldsymbol{Q}$ and $\boldsymbol{K}$ differ between the training phase and the decoding phase (as shown in the equation below). In the decoding phase, we cannot fully materialize the $\boldsymbol{K}$ from the training phase. In other words, QK-Norm cannot be performed during decoding.

Why use MLA? We have already discussed this in two articles, “Transformer Upgrade Path: 21, What Makes MLA Good? (Part 1)” and “Transformer Upgrade Path: 21, What Makes MLA Good? (Part 2)”, so it will not be repeated here. In short, we hope that MLA can also have a mechanism similar to QK-Norm that guarantees MaxLogit suppression.

Direct Approach

#

During this period, we also tried some indirect methods, such as individually lowering the learning rates of $\boldsymbol{Q}$ and $\boldsymbol{K}$, or separately increasing their Weight Decay, but none were effective. The closest we came to success was Partial QK-Norm. For MLA, its $\boldsymbol{Q}$ and $\boldsymbol{K}$ are divided into four parts: qr, qc, kr, and kc. Among these, the first three parts can be materialized during Decoding. Therefore, we applied RMSNorm to all three parts, which did suppress MaxLogit, but the length activation effect was very poor.

After multiple failures, we couldn’t help but reflect: our previous attempts were actually just “indirect means” to suppress MaxLogit. What is the direct means that truly guarantees solving MaxLogit explosion? From the inequality above, it’s not hard to associate that one could perform singular value clipping on $\boldsymbol{W}_q,\boldsymbol{W}_k$. However, this is still essentially an indirect method, and the computational cost of singular value clipping is not low.

However, it’s clear that post-hoc scaling of $\boldsymbol{W}_q,\boldsymbol{W}_k$ is theoretically feasible. The question is when to scale and by how much. Finally, one day, it dawned on the author: MaxLogit itself is the most direct signal to trigger scaling! Specifically, when MaxLogit exceeds the desired threshold $\tau$, we directly multiply $\boldsymbol{Q}\boldsymbol{K}^{\top}$ by $\gamma = \tau / S_{\max}$. Then the new MaxLogit will certainly not exceed $\tau$. The operation of multiplying by $\gamma$ can be absorbed into the weights of $\boldsymbol{Q}$ and $\boldsymbol{K}$ separately. Thus, we obtain the initial version of QK-Clip:

Where $S_{\max}^{(l)}$ is the MaxLogit of the $l$-th Attention layer, and $\boldsymbol{W}_q^{(l)}, \boldsymbol{W}_k^{(l)}$ are the weights of its $\boldsymbol{Q}$ and $\boldsymbol{K}$. That is, after the optimizer update, whether to clip the weights of $\boldsymbol{Q}$ and $\boldsymbol{K}$ is determined by the magnitude of $S_{\max}^{(l)}$. The clipping magnitude is directly determined by the ratio of $S_{\max}^{(l)}$ to the threshold $\tau$, directly ensuring that the clipped matrix no longer experiences MaxLogit explosion. At the same time, because it operates directly on the weights, it does not affect the inference mode, naturally making it compatible with MLA.

Fine-tuning

#

The initial version of QK-Clip indeed successfully suppressed MLA’s MaxLogit, but after carefully observing the model’s “internal state,” we found that it suffered from “over-clipping.” After fixing this problem, we arrived at the final version of QK-Clip.

We know that all Attention variants have multiple Heads. Initially, we monitored only one MaxLogit metric per Attention layer, where the Logits from all Heads were aggregated to take the maximum. This resulted in QK-Clip applying to all Heads together. However, when we separately monitored the MaxLogit for each Head, we found that in reality, only a few Heads per layer experienced MaxLogit explosion. If all Heads were clipped by the same ratio, most Heads would be “innocently affected,” which is the meaning of over-clipping.

Simply put, QK-Clip multiplies by a number less than 1. For a MaxLogit-exploding Head, this number just counteracts the growth trend. However, for other Heads, it is merely a reduction (they have no growth trend or a very weak one). Due to being pointlessly multiplied by a number less than 1 over a long period, it’s easy for values to approach zero, which is a symptom of “over-clipping.”

Therefore, to avoid “collateral damage,” we should monitor MaxLogit and perform QK-Clip on a Per-Head basis. However, another devilish detail is hidden here: the initial version of QK-Clip distributed the clipping factor evenly across $\boldsymbol{Q}$ and $\boldsymbol{K}$. But MLA’s $\boldsymbol{Q}$ and $\boldsymbol{K}$ have four parts: qr, qc, kr, and kc. Among these, kr is shared by all Heads. If it is clipped, the “collateral damage” problem would also arise. Therefore, for (qr, kr), we should only clip qr.

After the above adjustments, the final version of QK-Clip is:

Where the superscript ${}^{(l,h)}$ denotes the $l$-th layer and $h$-th Head.

Extension Path

#

At this point, the operational details of QK-Clip have been introduced. It directly uses our desired MaxLogit as a signal to make the smallest possible changes to the weights of $\boldsymbol{Q}$ and $\boldsymbol{K}$, achieving the effect of controlling the MaxLogit value within a specified threshold. At the same time, because this method directly modifies the weights, its compatibility is better than QK-Norm, and it can be used for MLA.

In the training of Kimi K2, we set the threshold $\tau$ to 100. The total training steps were approximately 220k steps. Starting from roughly 7k steps, Heads with MaxLogit exceeding $\tau$ began to appear. Subsequently, for a considerable period, Muon Update and QK-Clip engaged in a “tug-of-war,” with Muon attempting to increase MaxLogit and QK-Clip aiming to decrease it, maintaining a delicate balance. Interestingly, after 70k steps, the MaxLogit of all Heads voluntarily decreased below 100, and QK-Clip ceased to be effective.

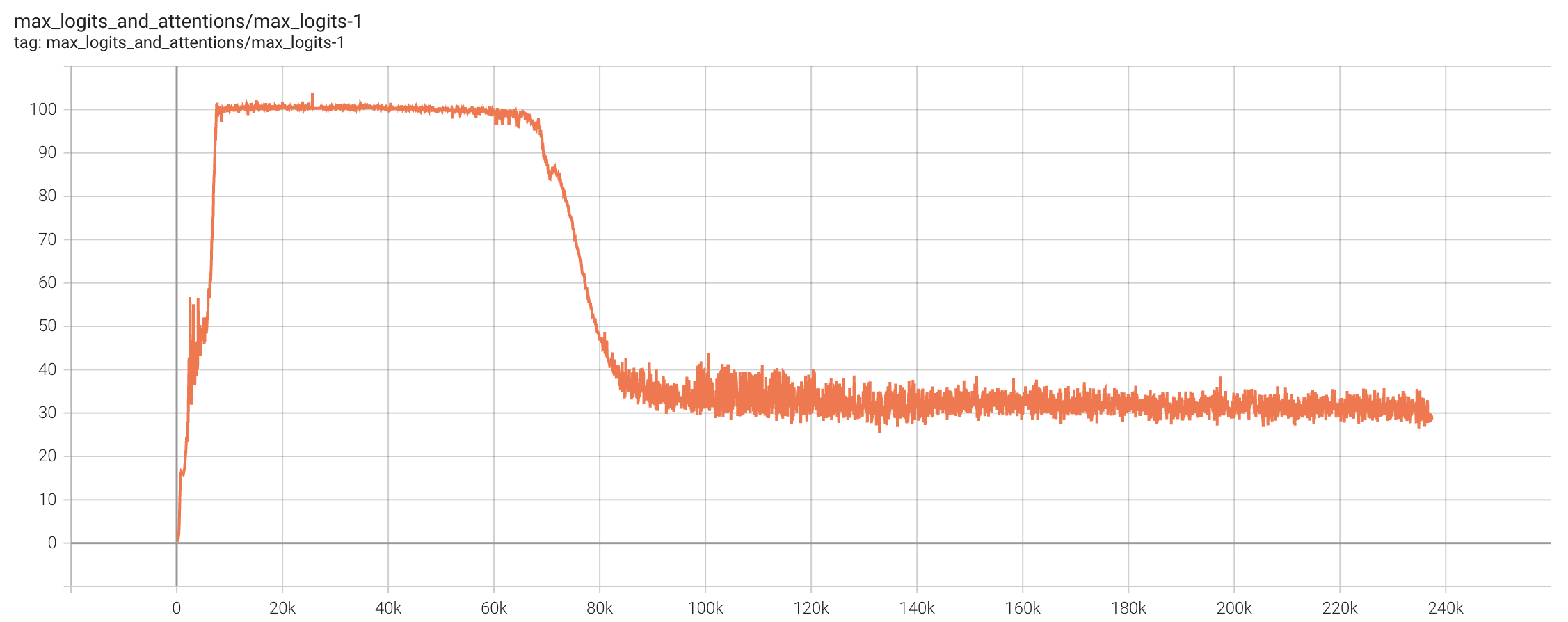
This indicates that under the effect of Weight Decay, as long as we can stabilize training, the model is likely to voluntarily reduce MaxLogit in the end. QK-Clip’s role is precisely to help the model smoothly navigate the early stages of training. Some readers might worry that QK-Clip could harm performance. However, we conducted comparative experiments on small models, and even when MaxLogit was suppressed significantly (e.g., to 30) via QK-Clip, no substantial difference in performance was observed. Combined with the phenomenon that the model voluntarily reduces MaxLogit in the mid-to-late stages, we have reason to believe that QK-Clip is lossless in terms of performance.

We also observed in our experiments that Muon generally tends to experience MaxLogit explosion more easily than Adam. Therefore, to some extent, QK-Clip is a supplementary update rule specifically for Muon; it is one of Muon’s “secret weapons” for ultra-large-scale training, which is also the meaning of this article’s title. To this end, we combined the Muon modifications proposed in our Moonlight paper with QK-Clip and named it “MuonClip” ($\boldsymbol{W}\in\mathbb{R}^{n\times m}$):

Note that “Muon generally tends to experience MaxLogit explosion more easily than Adam” does not mean only Muon will experience MaxLogit explosion. We know that DeepSeek-V3 was trained with Adam, and we also observed the MaxLogit explosion phenomenon in DeepSeek-V3’s open-source model. Additionally, Gemma2 used $\text{softcap}$ to prevent MaxLogit explosion, and it was also trained with Adam. Therefore, while we emphasize the value of QK-Clip for Muon, if readers insist on using Adam, it can also be combined with Adam to form AdamClip.

Reasoning

#

Why is Muon more prone to causing MaxLogit explosion? In this section, the author attempts to provide a theoretical explanation for your reference.

As can be seen from the inequality, MaxLogit explosion often implies signs of spectral norm explosion in $\boldsymbol{W}_q$ or $\boldsymbol{W}_k$. In fact, the definition of spectral norm also includes a $\max$ operation, so the two are essentially connected. Therefore, the problem can be transformed into “why Muon is more likely to cause spectral norm explosion.” We know that the spectral norm equals the largest singular value, so we can further infer “why Muon tends to increase singular values.”

What is the difference between Muon and Adam? The update quantity provided by Muon undergoes an $\msign$ operation, making all its singular values equal, meaning its effective rank is full rank; whereas for typical matrices, singular values usually vary in magnitude, with the first few singular values being dominant. From the perspective of effective rank, they are low rank, and our assumption for Adam’s update quantity is also such. This assumption is not new; for instance, Higher-Order muP also assumes the low-rank nature of Adam’s update quantity.

In terms of formulas, let the SVD of parameter $\boldsymbol{W}_{t-1}$ be $\sum_i \sigma_i \boldsymbol{u}_i \boldsymbol{v}_i^{\top}$, the SVD of Muon’s update quantity be $\sum_j \bar{\sigma}\bar{\boldsymbol{u}}_j \bar{\boldsymbol{v}}_j^{\top}$, and the SVD of Adam’s update quantity be $\sum_j \tilde{\sigma}_j\tilde{\boldsymbol{u}}_j \tilde{\boldsymbol{v}}_j^{\top}$. Then:

Clearly, if a singular vector pair $\boldsymbol{u}_i \boldsymbol{v}_i^{\top}$ is very close to some $\bar{\boldsymbol{u}}_j \bar{\boldsymbol{v}}_j^{\top}$ or $\tilde{\boldsymbol{u}}_j \tilde{\boldsymbol{v}}_j^{\top}$, they will directly superimpose, thereby increasing the singular values of $\boldsymbol{W}_t$. Since Muon’s update quantity is full rank, its “collision probability” with $\boldsymbol{W}_{t-1}$ will be much greater than Adam’s, which is why Muon is more likely to increase the singular values of parameters.

Of course, the above analysis is general and not limited to the weights of $\boldsymbol{Q}$ and $\boldsymbol{K}$. In fact, we have already verified in Moonlight that models trained with Muon generally have higher singular value entropy in their weights, which corroborates the above conjecture. The peculiarity of Attention Logit is that it is a bilinear form $\boldsymbol{q}_i\cdot \boldsymbol{k}_j = (\boldsymbol{x}_i \boldsymbol{W}_q)\cdot(\boldsymbol{x}_j \boldsymbol{W}_k)$. The consecutive multiplication of $\boldsymbol{W}_q$ and $\boldsymbol{W}_k$ significantly increases the risk of explosion, easily leading to a “worse gets worse” vicious cycle, ultimately contributing to MaxLogit explosion.

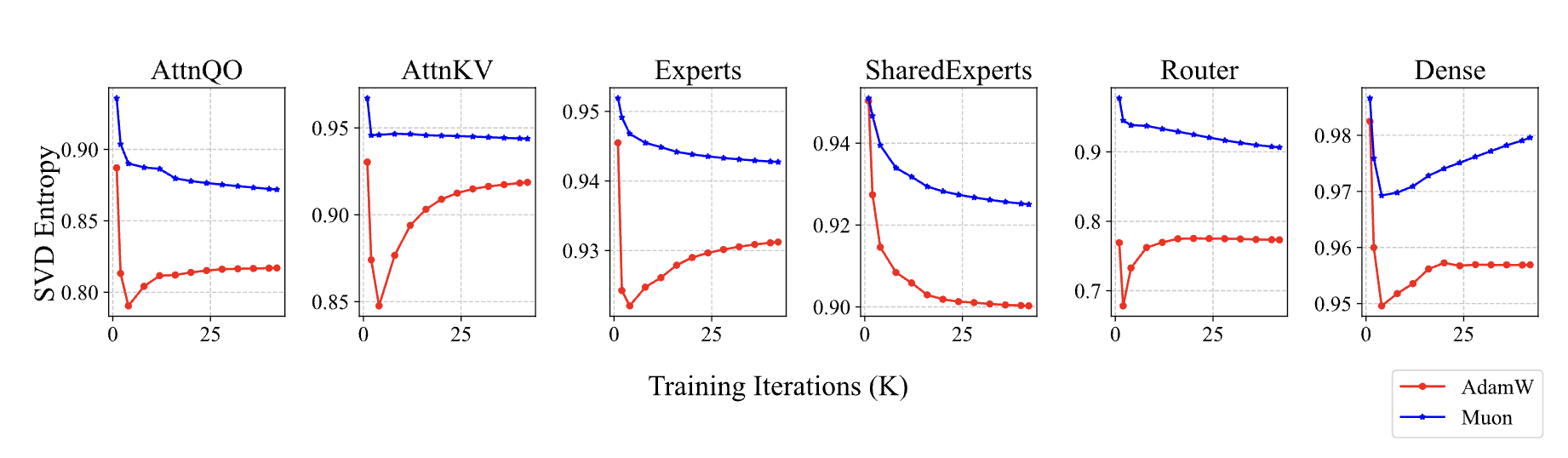
Finally, “Muon’s collision probability is much greater than Adam’s” is a relative statement. In reality, singular vectors colliding is still a low-probability event, which explains why only a small portion of Attention Heads experience MaxLogit explosion. This perspective can also explain a previously observed phenomenon in Moonlight: fine-tuning a model pre-trained with Muon/Adam using Adam/Muon, respectively, usually yields suboptimal results. This is because Muon’s training weights have a higher effective rank, while Adam’s updates are low-rank. With one high and one low, fine-tuning efficiency deteriorates. Conversely, Adam’s training weights have a lower effective rank, but Muon’s updates are full-rank, giving it a higher probability of interfering with small singular value components, causing the model to deviate from the low-rank local optimum of pre-training, thereby affecting fine-tuning efficiency.

Further Extensions

#

At this point, the important computational and experimental details regarding QK-Clip should be clear. It’s also worth noting that while the concept of QK-Clip is simple, implementing it in distributed training can be somewhat challenging due to the need for Per-Head clipping, as parameter matrices are often “fragmented” at this stage (it’s not too difficult to adapt it based on Muon, but slightly more complex for Adam).

For the author and their team, QK-Clip is not just a specific method for solving the MaxLogit explosion problem; it also represents a “sudden realization” after repeated failed attempts to solve the problem through indirect means: since there is a clear metric, we should seek direct approaches that guarantee a solution, rather than wasting time on ideas that might but not necessarily solve the problem, such as lowering LR, increasing Weight Decay, or partial QK-Norm.

From a methodological perspective, the idea behind QK-Clip is not limited to solving MaxLogit explosion; it can be seen as an “antibiotic” for many training instability problems. An “antibiotic,” in this context, refers to a method that might not be the most sophisticated solution but is often one of the most direct and effective ways to address a problem. QK-Clip possesses this characteristic; it can be generally extended to “clip where instability occurs.”

For example, in some cases, models might experience a “MaxOutput explosion” problem. In such situations, we could consider clipping the weight $\boldsymbol{W}_o$ based on the MaxOutput value. Analogous to QK-Clip’s Per-Head operation, we would also need to consider Per-Dim operations here. However, the cost of Per-Dim clipping is clearly too high, so a compromise might be necessary. In short, “clip where instability occurs” provides a unified problem-solving approach, but the specific details depend on individual implementation.

Finally, the practice of manually formulating update rules based on certain signals, like QK-Clip, was inspired to some extent by DeepSeek’s Loss-Free load balancing strategy. Here, we once again pay tribute to DeepSeek!

Summary (formatted)

#

This article introduces QK-Clip, a new approach to the MaxLogit explosion problem. Unlike QK-Norm, it is a post-hoc adjustment scheme for Q and K weights that does not alter the model’s forward computation, thus offering broader applicability. It is an important stabilization strategy for the “Muon + MLA” combination in ultra-large-scale training, and one of the key technologies for our newly released trillion-parameter model, Kimi K2.

@online{kexuefm-11126,
        title={QK-Clip: Advancing Muon Further on its Scale-up Journey},
        author={苏剑林},
        year={2025},
        month={07},
        url={\url{https://kexue.fm/archives/11126}},
}