1. SGD + Hypersphere

By Su Jianlin | August 1, 2025 | 5722 Readers

The description “the opposite direction of the gradient is the direction of steepest descent” is often used to introduce the principle of Stochastic Gradient Descent (SGD). However, this statement is conditional. For instance, “direction” in mathematics refers to a unit vector, which depends on the definition of “norm (magnitude).” Different norms lead to different conclusions. Muon essentially changed the spectral norm for matrix parameters, thereby deriving a new descent direction. Another example is when we transition from unconstrained optimization to constrained optimization, the direction of steepest descent may not necessarily be the opposite direction of the gradient.

To this end, in this article, we will start a new series, focusing on “constraints” as the main theme, to re-examine the proposition of “steepest descent” and explore where the “direction of steepest descent” points under different conditions.

Optimization Principle

#

As the first article, we start with SGD to understand the mathematical meaning behind the statement “the opposite direction of the gradient is the direction of steepest descent,” and then apply it to optimization on a hypersphere. Before that, I would also like to revisit the “Least Action Principle” for optimizers, as proposed in “Muon Sequel: Why Did We Choose to Try Muon?”.

Here, $\mathcal{L}$ is the loss function, $\boldsymbol{w}\in\mathbb{R}^n$ is the parameter vector, $\Delta \boldsymbol{w}$ is the update amount, and $\rho(\Delta\boldsymbol{w})$ is some measure of the magnitude of the update amount $\Delta\boldsymbol{w}$. The above objective is intuitive: to find the update amount that maximally decreases the loss function (fast) under the premise that the “step size” does not exceed $\eta$ (stable). This is the mathematical meaning of the “Least Action Principle” and also the mathematical meaning of “steepest descent.”

Objective Transformation

#

Assuming $\eta$ is sufficiently small, $\Delta\boldsymbol{w}$ is also sufficiently small such that a first-order approximation is accurate enough. We can then replace $\mathcal{L}(\boldsymbol{w} +\Delta\boldsymbol{w})$ with $\mathcal{L}(\boldsymbol{w}) + \langle\boldsymbol{g},\Delta\boldsymbol{w}\rangle$, where $\boldsymbol{g} = \nabla_{\boldsymbol{w}}\mathcal{L}(\boldsymbol{w})$, yielding the equivalent objective:

This simplifies the optimization objective into a linear function of $\Delta \boldsymbol{w}$, reducing the difficulty of solving. Furthermore, let $\Delta \boldsymbol{w} = -\kappa \boldsymbol{\phi}$, where $\rho(\boldsymbol{\phi})=1$. Then the above objective is equivalent to:

Assuming we can find at least one $\boldsymbol{\phi}$ satisfying the condition such that $\langle\boldsymbol{g},\boldsymbol{\phi}\rangle\geq 0$, then $\max\limits_{\kappa\in[0,\eta]} \kappa\langle\boldsymbol{g},\boldsymbol{\phi}\rangle = \eta\langle\boldsymbol{g},\boldsymbol{\phi}\rangle$. This means that the optimization for $\kappa$ can be solved beforehand, resulting in $\kappa=\eta$, which ultimately leaves only the optimization for $\boldsymbol{\phi}$:

Here, $\boldsymbol{\phi}$ satisfies the condition that some “magnitude” $\rho(\boldsymbol{\phi})$ equals 1, thus it represents the definition of some “direction vector.” Maximizing its inner product with the gradient $\boldsymbol{g}$ means finding the direction that causes the loss to decrease fastest (i.e., the opposite direction of $\boldsymbol{\phi}$).

Gradient Descent

#

From the preceding equation, it can be seen that for the “direction of steepest descent,” the only uncertainty is the measure $\rho$. This is a fundamental prior (Inductive Bias) within optimizers, and different measures will yield different directions of steepest descent. The simplest case is the L2 norm or Euclidean norm, $\rho(\boldsymbol{\phi})=\Vert \boldsymbol{\phi} \Vert_2$, which is our usual definition of magnitude. In this case, we have the Cauchy-Schwarz inequality:

The condition for equality to hold is $\boldsymbol{\phi} \propto\boldsymbol{g}$. Combined with the condition that the magnitude is 1, we get $\boldsymbol{\phi}=\boldsymbol{g}/\Vert\boldsymbol{g}\Vert_2$, which is precisely the direction of the gradient. Therefore, the premise for “the opposite direction of the gradient is the direction of steepest descent” is that the chosen measure is the Euclidean norm. More generally, we consider the $p$-norm:

The Cauchy-Schwarz inequality can be generalized to the Hölder’s inequality:

The condition for equality to hold is $\boldsymbol{\phi}^{[p]} \propto\boldsymbol{g}^{[q]}$, which leads to the solution:

The optimizer that uses this as its direction vector is called pbSGD, from “pbSGD: Powered Stochastic Gradient Descent Methods for Accelerated Non-Convex Optimization”. It has two special cases: first, when $p=q=2$, it degenerates into SGD; second, when $p\to\infty$, then $q\to 1$, at which point $|g_i|^{q/p}\to 1$, and the update direction becomes the sign function of the gradient, i.e., SignSGD.

On the Hypersphere

#

In the previous discussion, we only imposed constraints on the parameter increment $\Delta\boldsymbol{w}$. Next, we want to add constraints to the parameter $\boldsymbol{w}$ itself. Specifically, we assume that the parameter $\boldsymbol{w}$ lies on a unit sphere, and we want the updated parameter $\boldsymbol{w}+\Delta\boldsymbol{w}$ to also remain on the unit sphere (refer to “Hypersphere”). Starting from the core objective, we can write the new objective as:

We still adhere to the principle that “$\eta$ is sufficiently small, and a first-order approximation is sufficient,” yielding:

Therefore, this is equivalent to transforming the constraint into the linear form $\langle \boldsymbol{w}, \boldsymbol{\phi}\rangle=0$. To solve the new objective, we introduce the Lagrange multiplier $\lambda$, and write:

The condition for equality to hold is $\boldsymbol{\phi}\propto \boldsymbol{g} + \lambda\boldsymbol{w}$. Combined with the conditions $\Vert\boldsymbol{\phi}\Vert_2=1,\langle \boldsymbol{w}, \boldsymbol{\phi}\rangle=0,\Vert\boldsymbol{w}\Vert_2=1$, we can solve for:

Note that now we have $\Vert\boldsymbol{w}\Vert_2=1$ and $\Vert\boldsymbol{\phi}\Vert_2=1$, and $\boldsymbol{w}$ and $\boldsymbol{\phi}$ are orthogonal. In this case, the magnitude of $\boldsymbol{w} - \eta\boldsymbol{\phi}$ is not exactly equal to 1, but rather $\sqrt{1 + \eta^2}=1 + \eta^2/2 + \cdots$, accurate to $\mathcal{O}(\eta^2)$. This is consistent with our earlier assumption that “the first-order term of $\eta$ is sufficient.” If one wants the magnitude of the updated parameters to be strictly equal to 1, an additional retraction step can be added to the update rule:

Geometric Interpretation

#

Just now, by applying the “first-order approximation is sufficient” principle, we simplified the nonlinear constraint $\Vert\boldsymbol{w}-\eta\boldsymbol{\phi}\Vert_2 = 1$ to the linear constraint $\langle \boldsymbol{w}, \boldsymbol{\phi}\rangle=0$. The geometric meaning of the latter is “perpendicular to $\boldsymbol{w}$.” There is also a more professional term for this: the “tangent space” of $\Vert\boldsymbol{w}\Vert_2=1$. The operation $\boldsymbol{g} - \langle \boldsymbol{g}, \boldsymbol{w}\rangle\boldsymbol{w}$ precisely corresponds to projecting the gradient $\boldsymbol{g}$ onto the tangent space.

Therefore, fortunately, SGD on a sphere has a very clear geometric interpretation, as shown in the figure below:

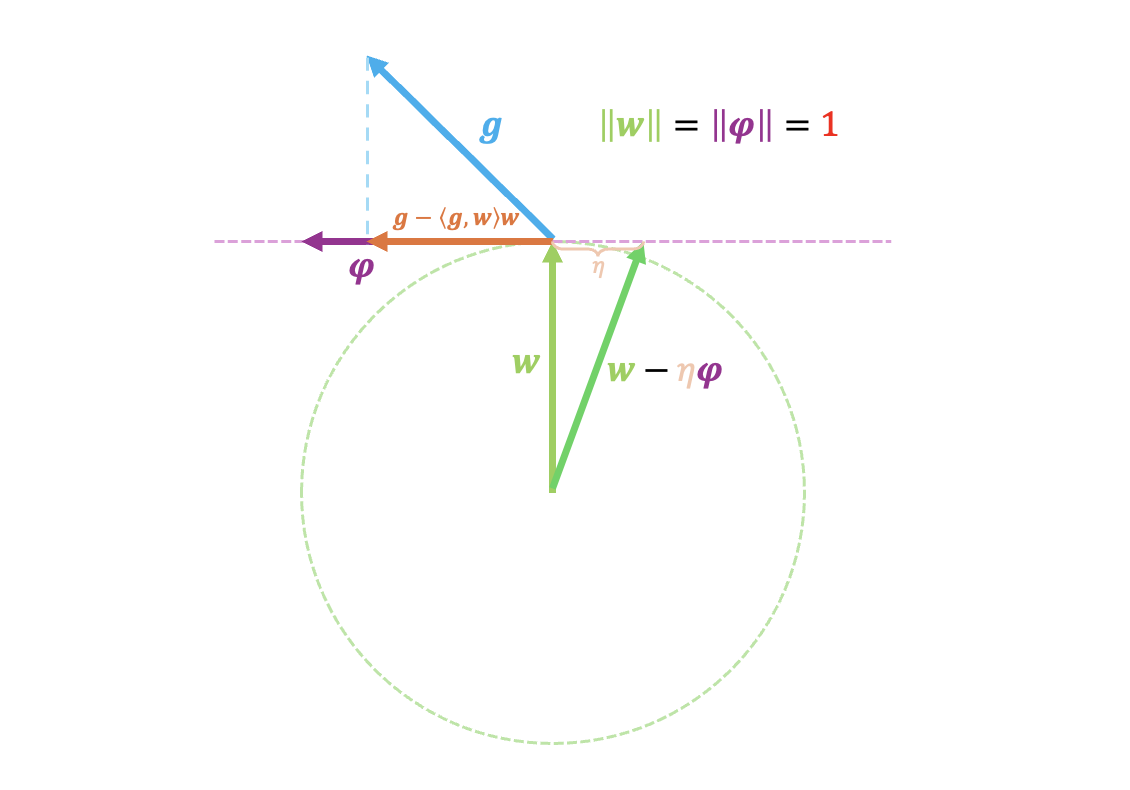
I believe many readers appreciate this geometric perspective; it is indeed pleasing to the eye. However, I must remind everyone that priority should be given to thoroughly understanding the algebraic solution process, because a clear geometric interpretation is often a luxury, something that is serendipitous, and in most cases, the complex algebraic process is the essence.

General Results

#

Next, some readers might want to generalize this to the general $p$-norm, right? Let’s try it together and see what difficulties we encounter. In this case, the problem is:

A first-order approximation transforms $\Vert\boldsymbol{w}-\eta\boldsymbol{\phi}\Vert_p = 1$ into $\langle\boldsymbol{w}^{[p-1]},\boldsymbol{\phi}\rangle = 0$, then introduces the Lagrange multiplier $\lambda$:

The condition for equality to hold is:

So far, there are no substantial difficulties. However, next we need to find $\lambda$ such that $\langle\boldsymbol{w}^{[p-1]},\boldsymbol{\phi}\rangle = 0$. When $p \neq 2$, this is a complex nonlinear equation for which there is no straightforward solution method (though, once solved, we are guaranteed to obtain the optimal solution, as guaranteed by Hölder’s inequality). Therefore, for general $p$, we can only stop here. We will explore numerical solution methods specifically when we encounter instances where $p\neq 2$.

Besides $p=2$, we can also attempt to solve for $p\to\infty$. In this case, $\boldsymbol{\phi}=\operatorname{sign}(\boldsymbol{g} + \lambda\boldsymbol{w}^{[p-1]})$, and the condition $\Vert\boldsymbol{w}\Vert_p=1$ implies that the maximum value among $|w_1|,|w_2|,\cdots,|w_n|$ is equal to 1. If we further assume that there is only one maximum value, then $\boldsymbol{w}^{[p-1]}$ is a one-hot vector, with $\pm 1$ at the position of the maximum absolute value and zeros elsewhere. In this case, $\lambda$ can be solved, and the result is to clip the gradient at the maximum value’s position to zero.

Summary (formatted)

#

This article starts a new series, primarily discussing optimization problems centered on “equality constraints,” attempting to find the “direction of steepest descent” for some common constraint conditions. As the first article, this paper discusses variants of SGD under “hypersphere” constraints.

@online{kexuefm-11196,
        title={Steepest Descent on Manifolds: 1. SGD + Hypersphere},
        author={苏剑林},
        year={2025},
        month={08},
        url={\url{https://kexue.fm/archives/11196}},
}