Why Add Short Conv to Linear Attention?

If readers have been following advancements in model architecture, they will find that newer linear Attention models (refer to “A Brief History of Linear Attention: From Imitation, Innovation to Feedback”) have added Short Convs to $\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}$, as shown in the DeltaNet example below:

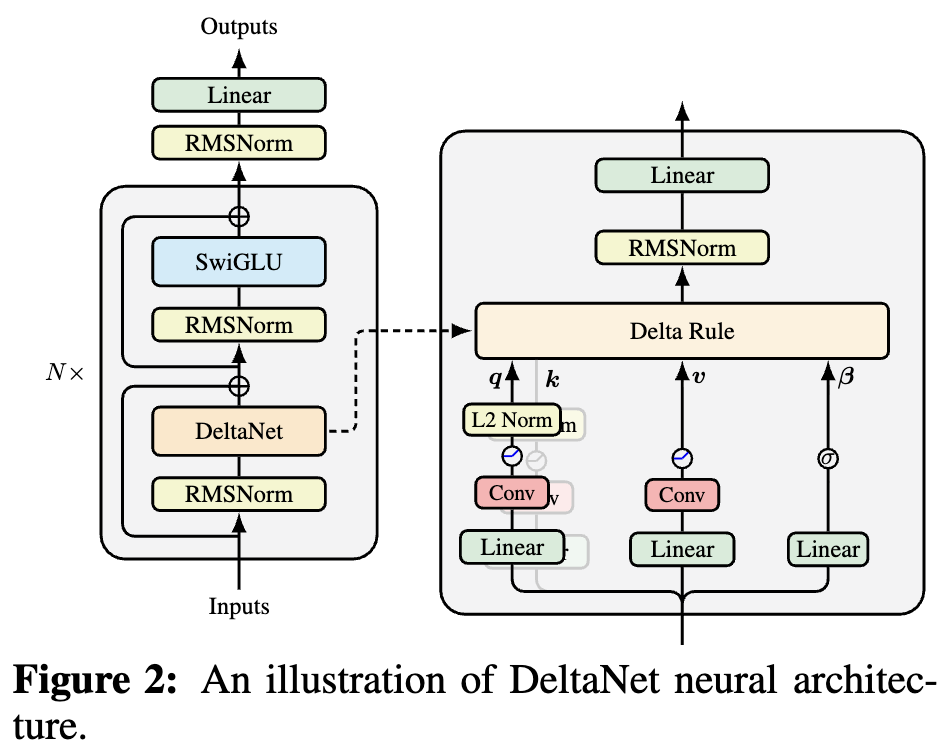
Why add this Short Conv? An intuitive understanding might be to increase model depth, enhance the model’s Token-Mixing capability, etc. In essence, it’s to compensate for the reduced expressive power caused by linearization. This explanation is generally correct, but it’s a “one-size-fits-all” answer. We want a more precise understanding of its operating mechanism.

Next, the author will provide their own understanding (or more precisely, a conjecture).

Test-Time Training

#

From “A Brief History of Linear Attention: From Imitation, Innovation to Feedback”, we know that the core idea behind current new linear Attention models is TTT (Test-Time Training) or Online Learning. TTT leverages the similarity between optimizer updates and RNN iterations to build (not necessarily linear) RNN models. Linear Attention variants such as DeltaNet, GDN, and Comba can all be seen as its special cases.

Specifically, TTT treats $\boldsymbol{K},\boldsymbol{V}$ as paired corpus $(\boldsymbol{k}_1, \boldsymbol{v}_1),(\boldsymbol{k}_2, \boldsymbol{v}_2),\cdots,(\boldsymbol{k}_t, \boldsymbol{v}_t)$. We use this to train a model $\boldsymbol{v} = \boldsymbol{f}(\boldsymbol{S}_t;\boldsymbol{k})$, and then output $\boldsymbol{o}_t = \boldsymbol{f}(\boldsymbol{S}_t;\boldsymbol{q}_t)$, where $\boldsymbol{S}_t$ are the model parameters, updated by SGD:

Of course, if we wish, we can also consider other optimizers. For example, “Test-Time Training Done Right” experimented with the Muon optimizer. Besides changing the optimizer, other flexible aspects include the architecture of the model $\boldsymbol{v} = \boldsymbol{f}(\boldsymbol{S}_t;\boldsymbol{k})$ and the loss function $\mathcal{L}(\boldsymbol{f}(\boldsymbol{S}_{t-1};\boldsymbol{k}_t), \boldsymbol{v}_t)$. Furthermore, we can consider Mini-batch TTT with chunks as units.

It’s not hard to imagine that, in theory, TTT offers very high flexibility, allowing for the construction of arbitrarily complex RNN models. When the architecture chooses a linear model $\boldsymbol{v} = \boldsymbol{S}_t\boldsymbol{k}$ and the loss function chooses squared error, the result corresponds to DeltaNet; if we add some regularization terms, variants like GDN can be derived.

The Crucial Question

#

Placing TTT upfront primarily aims to show that the underlying logic of current mainstream linear Attention is the same as TTT, centered on Online Learning of corpus pairs $(\boldsymbol{k}_1, \boldsymbol{v}_1),(\boldsymbol{k}_2, \boldsymbol{v}_2),\cdots,(\boldsymbol{k}_t, \boldsymbol{v}_t)$. This naturally leads to a question: Why do this? What exactly is learned by doing this?

To answer this question, we first need to reflect on “what exactly we want.” According to the characteristics of Softmax Attention, what we want is to compute an $\boldsymbol{o}_t$ based on $(\boldsymbol{k}_1, \boldsymbol{v}_1),(\boldsymbol{k}_2, \boldsymbol{v}_2),\cdots,(\boldsymbol{k}_t, \boldsymbol{v}_t)$ and $\boldsymbol{q}_t$. Ideally, this process should depend on all $(\boldsymbol{k},\boldsymbol{v})$. At the same time, we also hope to achieve this goal with constant complexity. Therefore, an intuitive idea is to first compress $(\boldsymbol{k},\boldsymbol{v})$ into a fixed-size State (independent of $t$), and then read this State.

How is this compression achieved? TTT’s idea is: design a model $\boldsymbol{v} = \boldsymbol{f}(\boldsymbol{S}_t;\boldsymbol{k})$, and then use these $(\boldsymbol{k},\boldsymbol{v})$ pairs to “train” this model. After training, the model, in a sense, “memorizes” these $(\boldsymbol{k},\boldsymbol{v})$ pairs, which is equivalent to compressing all $(\boldsymbol{k},\boldsymbol{v})$ into the fixed-size model weights $\boldsymbol{S}_t$. As for how $\boldsymbol{q}_t$ utilizes $\boldsymbol{S}_t$, directly substituting it into the model to get $\boldsymbol{o}_t = \boldsymbol{f}(\boldsymbol{S}_t;\boldsymbol{q}_t)$ is a relatively natural choice, but in principle, we could also design other ways of utilization.

In other words, TTT’s core task is to leverage the idea that “training a model” is approximately equivalent to “memorizing the training set” to achieve the compression of $\boldsymbol{K},\boldsymbol{V}$. However, this equivalence of “training a model” and “memorizing the training set” is not so trivial; it has some preconditions.

Key-Value Homogeneity

#

For example, if we take $\boldsymbol{K}=\boldsymbol{V}$, then the TTT framework would theoretically fail. This is because the optimal solution for the model $\boldsymbol{v} = \boldsymbol{f}(\boldsymbol{S}_t;\boldsymbol{k})$ would be an identity transformation, a trivial solution, which means nothing is memorized. Online-updating models like DeltaNet might still be salvageable, but models based on exact solutions like MesaNet would indeed directly output the identity matrix $\boldsymbol{I}$.

Some readers might retort: Why consider an unscientific choice like $\boldsymbol{K}=\boldsymbol{V}$ out of the blue? Indeed, $\boldsymbol{K}=\boldsymbol{V}$ is a rather extreme choice; it’s used here merely as an example to illustrate that “training a model” being approximately equivalent to “memorizing the training set” is not arbitrarily true. Furthermore, we have already verified in “The Road to Transformer Upgrades: 20, What’s Good About MLA? (Part 1)” that for Softmax Attention, $\boldsymbol{K}=\boldsymbol{V}$ can also yield decent results.

This indicates that $\boldsymbol{K}=\boldsymbol{V}$ is not an inherent obstacle for the Attention mechanism, yet it can lead to model failure within the TTT framework. This is because if $\boldsymbol{K}$ and $\boldsymbol{V}$ completely overlap, there’s nothing to learn from the regression between them. Similarly, we can imagine that the higher the information overlap between $\boldsymbol{K}$ and $\boldsymbol{V}$, the less there is to learn between them, meaning TTT’s memorization of the “training set” will be lower.

In general Attention mechanisms, $\boldsymbol{q}_t,\boldsymbol{k}_t,\boldsymbol{v}_t$ are all derived from the same input $\boldsymbol{x}_t$ through different linear projections. In other words, $\boldsymbol{k}_t,\boldsymbol{v}_t$ share the same source $\boldsymbol{x}_t$, which always gives the feeling of “predicting oneself,” limiting what can be learned.

Convolution to the Rescue

#

How can TTT learn more valuable results when keys and values share the same source, or even when $\boldsymbol{K}=\boldsymbol{V}$? The answer has actually existed for a long time—traceable back to Word2Vec and even earlier—which is not to “predict oneself,” but to “predict surroundings.”

Taking Word2Vec as an example, we know its training method is “predicting context from a center word”; the previously popular BERT uses MLM as its pre-training method, where certain words are masked to predict those words, which can be described as “predicting center words from context”; current mainstream LLMs use NTP (Next Token Prediction) as their training task, predicting the next word based on the preceding context. Clearly, their common characteristic is not predicting oneself, but predicting surroundings.

Therefore, to improve TTT, we must change the “predicting oneself” pairing method like $(\boldsymbol{k}_t,\boldsymbol{v}_t)$. Given that current LLMs primarily use NTP, we can also consider NTP in TTT, for example, by constructing corpus pairs with $(\boldsymbol{k}_{t-1},\boldsymbol{v}_t)$, i.e., using $\boldsymbol{k}_{t-1}$ to predict $\boldsymbol{v}_t$. This way, even if $\boldsymbol{K}=\boldsymbol{V}$, non-trivial results can be learned. At this point, both inside and outside TTT are NTP tasks, showing beautiful consistency.

However, if we only use $\boldsymbol{k}_{t-1}$ to predict $\boldsymbol{v}_t$, it seems $\boldsymbol{k}_t$ is wasted. So, a further idea is to somehow mix $\boldsymbol{k}_{t-1}$ and $\boldsymbol{k}_t$ before predicting $\boldsymbol{v}_t$. At this point, it might click for everyone: “mixing $\boldsymbol{k}_{t-1}$ and $\boldsymbol{k}_t$ in some way” is equivalent to a Conv with kernel_size=2! Therefore, adding Short Conv to $\boldsymbol{K}$ transforms TTT’s training objective from “predicting oneself” to NTP, allowing TTT to at least learn an n-gram model.

As for adding Short Conv to $\boldsymbol{Q},\boldsymbol{V}$, it’s entirely incidental. According to information from “Feilaige”, while adding it to $\boldsymbol{Q},\boldsymbol{V}$ also has some effect, the improvement is far less significant than that brought by adding Short Conv to $\boldsymbol{K}$. This serves as further evidence for our conjecture.

Summary (formatted)

#

This article provides an understanding, arrived at through independent thinking, of the question “Why add Short Conv to linear Attention?”

@online{kexuefm-11320,
        title={Why Add Short Conv to Linear Attention?},
        author={苏剑林},
        year={2025},
        month={10},
        url={\url{https://kexue.fm/archives/11320}},
}