This is a gemini-2.5-flash translation of a Chinese article.
It has NOT been vetted for errors. You should have the original article open in a parallel tab at all times.
Yesterday, we discussed some counter-intuitive phenomena related to $n$-dimensional vectors in a group chat. One topic was that “two random vectors in $n$-dimensional space are almost always orthogonal,” which deviates significantly from our perception in 2D/3D space. To understand this conclusion theoretically, we can consider the distribution of the angle $\theta$ between two random vectors and calculate its mean and variance.
Probability Density#
First, let’s derive the probability density function for $\theta$. Well, actually, there’s not much derivation needed; it’s a direct consequence of $n$-dimensional hyperspherical coordinates.
To find the distribution of the angle between two random vectors, it’s evident that due to isotropy, we only need to consider unit vectors. And also due to isotropy, we only need to fix one vector and consider the other vector varying randomly. Without loss of generality, consider the random vector as
$$ \begin{equation}\boldsymbol{x}=(x_1,x_2,\dots,x_n)\end{equation} $$and the fixed vector as
$$ \begin{equation}\boldsymbol{y}=(1,0,\dots,0)\end{equation} $$Transform $\boldsymbol{x}$ into hyperspherical coordinates (for knowledge about $n$-dimensional spheres, refer to Wikipedia):
$$ \begin{equation} \left\{\begin{aligned} x_{1}&=\cos(\varphi_{1})\\ x_{2}&=\sin(\varphi_{1})\cos(\varphi_{2})\\ x_{3}&=\sin(\varphi_{1})\sin(\varphi_{2})\cos(\varphi_{3})\\ &\,\,\vdots \\ x_{n-1}&=\sin(\varphi_{1})\cdots \sin(\varphi_{n-2})\cos(\varphi_{n-1})\\ x_{n}&=\sin(\varphi_{1})\cdots \sin(\varphi_{n-2})\sin(\varphi_{n-1}) \end{aligned}\right. \end{equation} $$where $\varphi_{n−1}\in [0, 2\pi)$ and the range for the remaining $\varphi$ is $[0, \pi]$. At this point, the angle between $\boldsymbol{x}$ and $\boldsymbol{y}$ is:
$$ \begin{equation}\arccos \langle \boldsymbol{x},\boldsymbol{y}\rangle = \arccos \cos(\varphi_{1}) = \varphi_{1} \end{equation} $$This means the angle between the two is exactly $\varphi_1$. Then, the probability that the angle between $\boldsymbol{x}$ and $\boldsymbol{y}$ does not exceed $\theta$ is:
$$ \begin{equation}P_n(\varphi_1\leq\theta) = \frac{\text{Integral over the }n\text{-dimensional hypersphere where }\varphi_1\text{ does not exceed }\theta}{\text{Total integral over the }n\text{-dimensional hypersphere}} \end{equation} $$The integral element on the $n$-dimensional hypersphere is $\sin^{n-2}(\varphi_{1})\sin^{n-3}(\varphi_{2})\cdots \sin(\varphi_{n-2})\,d\varphi_{1}\,d\varphi_{2}\cdots d\varphi_{n-1}$ (can be found on Wikipedia), thus
$$ \begin{equation}\begin{aligned} P_n(\varphi_1\leq\theta) =& \frac{\int_0^{2\pi}\cdots\int_0^{\pi}\int_0^{\theta}\sin^{n-2}(\varphi_{1})\sin^{n-3}(\varphi_{2})\cdots \sin(\varphi_{n-2})\,d\varphi_{1}\,d\varphi_{2}\cdots d\varphi_{n-1}}{\int_0^{2\pi}\cdots\int_0^{\pi}\int_0^{\pi}\sin^{n-2}(\varphi_{1})\sin^{n-3}(\varphi_{2})\cdots \sin(\varphi_{n-2})\,d\varphi_{1}\,d\varphi_{2}\cdots d\varphi_{n-1}}\\ =& \frac{\text{Surface area of an }(n-1)\text{-dimensional unit hypersphere}\times\int_0^{\theta}\sin^{n-2}\varphi_{1} d\varphi_1}{\text{Surface area of an }n\text{-dimensional unit hypersphere}}\\ =& \frac{\Gamma\left(\frac{n}{2}\right)}{\Gamma\left(\frac{n-1}{2}\right)\sqrt{\pi}} \int_0^{\theta}\sin^{n-2}\varphi_1 d\varphi_1 \end{aligned} \end{equation} $$This indicates that the probability density function for $\theta$ is
$$ \begin{equation} p_n(\theta) = \frac{\Gamma\left(\frac{n}{2}\right)}{\Gamma\left(\frac{n-1}{2}\right)\sqrt{\pi}}\sin^{n-2} \theta \end{equation} $$Sometimes we are interested in the distribution of $\eta=\cos\theta$. In this case, we need to perform a change of variables for the probability density.
$$ \begin{equation}\begin{aligned} p_n(\eta)=&\frac{\Gamma\left(\frac{n}{2}\right)}{\Gamma\left(\frac{n-1}{2}\right)\sqrt{\pi}}\sin^{n-2} (\arccos\eta)\left|\frac{d\theta}{d\eta}\right|\\ =&\frac{\Gamma\left(\frac{n}{2}\right)}{\Gamma\left(\frac{n-1}{2}\right)\sqrt{\pi}}(1-\eta^2)^{(n-3)/2}\\ \end{aligned}\end{equation} $$Distribution Characteristics#
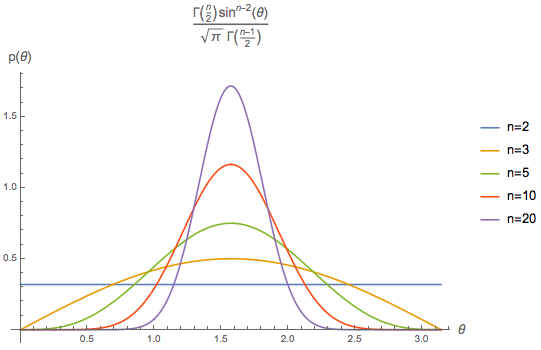
From the probability density functions derived above, we can see that when $n=2$, the distribution of the angle $\theta$ is uniform, and when $n=3$, the distribution of the cosine of the angle, $\cos\theta$, is uniform. These two results indicate that in the 2D and 3D spaces we perceive, the distribution of angles is relatively uniform. But what happens when $n$ is large? For example, $n=20, 50$?
From the form of $p_n(\theta)\sim\sin^{n-2}\theta$, it can be observed that when $n\geq 3$, the maximum probability occurs at $\theta=\frac{\pi}{2}$ (i.e., 90 degrees). Furthermore, $\sin^{n-2}\theta$ is symmetric about $\theta=\frac{\pi}{2}$, so its mean is also $\frac{\pi}{2}$. However, this does not fully describe the distribution; we also need to consider the variance:
$$ \begin{equation} Var_n(\theta) = \frac{\Gamma\left(\frac{n}{2}\right)}{\Gamma\left(\frac{n-1}{2}\right)\sqrt{\pi}}\int_0^{\pi}\left(\theta-\frac{\pi}{2}\right)^2\sin^{n-2} \theta d\theta\end{equation} $$This integral has an analytical solution, but its form is quite complicated (you can calculate it yourself using Mathematica if you’re interested). Let’s just look at some numerical solutions:
$$ \begin{array}{c|c} \hline n & \text{Variance}\\ \hline 3 & 0.467401\\ 10 & 0.110661\\ 20 & 0.0525832\\ 50 & 0.0204053\\ 100 & 0.0101007\\ 200 & 0.00502508\\ 1000 & 0.001001\\ \hline \end{array} $$It can be seen that as $n$ increases, the variance becomes smaller and smaller. This means that the angles between any two vectors in high-dimensional space are almost all concentrated around $\frac{\pi}{2}$. In other words, any two vectors in high-dimensional space are almost orthogonal.
Of course, this can also be seen from the graph:
$$ \begin{equation}\ln \sin^{n-2}\theta=\frac{2-n}{2}\left(\theta - \frac{\pi}{2}\right)^2 + \mathcal{O}\left(\left(\theta - \frac{\pi}{2}\right)^4\right)\end{equation} $$Readers who want an approximate analytical solution can consider using Laplace’s method to approximate $p_n(\theta)$ with a Gaussian distribution. Expand $\ln \sin^{n-2}\theta$ at $\theta=\frac{\pi}{2}$:
i.e.,
$$ \begin{equation}\sin^{n-2}\theta\approx \exp\left[-\frac{n-2}{2}\left(\theta - \frac{\pi}{2}\right)^2\right]\end{equation} $$From this approximate form, we can approximately consider $\theta$ to follow a normal distribution with a mean of $\frac{\pi}{2}$ and a variance of $\frac{1}{n-2}$. That is, when $n$ is large, the variance is approximately $\frac{1}{n-2}$. This also shows that as $n$ increases, the variance decreases.
Summary (formatted)#
This article derived the distribution of angles in high-dimensional space. It is recorded here for future reference, and also for the reference of interested readers.
@online{kexuefm-7076,
title={Distribution of the Angle Between Two Random Vectors in $n$-Dimensional Space},
author={苏剑林},
year={2019},
month={11},
url={\url{https://kexue.fm/archives/7076}},
}