'Rounding' Surpasses VQ-VAE

Just like “XXX is all you need,” many papers are titled “An Embarrassingly Simple XXX.” However, in my opinion, most of these papers are more hype than substance. Nevertheless, a recent paper I read truly made me exclaim, “It’s embarrassingly simple!” ~

The paper’s title is 《Finite Scalar Quantization: VQ-VAE Made Simple》. As the name suggests, it’s a work aiming to simplify VQ-VAE using FSQ (Finite Scalar Quantization). With the growing popularity of generative models and multimodal LLMs, VQ-VAE and its subsequent works have also “risen with the tide” as “image tokenizers.” However, VQ-VAE training itself has some issues, and this FSQ paper claims to achieve the same goal through simpler “rounding,” with the advantages of better performance, faster convergence, and more stable training.

Is FSQ really that magical? Let’s explore it together.

VQ

#

First, let’s understand “VQ.” VQ stands for “Vector Quantization” and refers to a technique that maps infinite, continuous encoding vectors to finite, discrete integer numbers. If we apply VQ to the intermediate layer of an autoencoder, we can compress the input size while making the encoded result a discrete integer sequence.

Assuming the autoencoder’s reconstruction loss is satisfactory, this integer sequence becomes the equivalent of the original image. All operations on the original image can then be transformed into operations on the integer sequence. For instance, if we want to train an image generation model, we only need to train an integer sequence generation model, which is equivalent to text generation. Thus, we can use it to train a GPT model, with the model and process being identical to text. After training, we can sample integer sequences from the GPT model and send them to the decoder to obtain images, thereby completing the construction of an image generation model. In short, “VQ + autoencoder” converts any input into an integer sequence consistent with text, unifying the input format of different modalities and their processing and generation models.

Such an autoencoder with VQ functionality is called a “VQ-VAE.”

AE

#

As early as four years ago, in the article 《A Concise Introduction to VQ-VAE: Quantized Autoencoders》, we introduced VQ-VAE. Despite bearing the name “VAE (Variational AutoEncoder),” it actually has little to do with VAE; as mentioned in the previous section, it is merely an AE (AutoEncoder) with VQ functionality.

Since it’s an AE, it has an encoder and a decoder. A typical AE looks like this:

VQ-VAE is slightly more complex:

Let’s explain it step by step. First, the initial step is the same: input $x$ into the encoder, outputting the encoding vector $z$. However, we don’t directly feed $z$ into the decoder. Instead, we first maintain a codebook $\{e_1,e_2,\cdots,e_K\}$, from which we select the $e_k$ closest to $z$ and feed it into the decoder to reconstruct $x$. Since the codebook is finite, we can also interpret the actual encoding result as an integer (i.e., the $k$ of the $e_k$ closest to $z$). This is the meaning of “VQ” in VQ-VAE.

Of course, in practical applications, to ensure reconstruction clarity, the encoder’s output might be multiple vectors. Each vector undergoes the same quantization step to become an integer. Thus, a picture originally in continuous real space is encoded by VQ-VAE into a sequence of integers, similar to the function of a text tokenizer, hence the term “image tokenizer.”

Gradients

#

However, because $\mathop{\text{argmin}}$ appears in the entire forward computation process, gradients cannot be backpropagated to the encoder, meaning we cannot optimize the encoder. A common approach here is Gumbel Softmax, but its effect is usually suboptimal. Therefore, the authors ingeniously leveraged Straight-Through to design better gradients for VQ-VAE. One could say this is the most brilliant part of VQ-VAE; it tells us that “Attention is all you need” is illusory, and “Gradient” is the real “all we need”!

Specifically, VQ-VAE uses the stop_gradient function (i.e., $\text{sg}$ in the formula), which is built into most deep learning frameworks, to define custom gradients. Any input passed through $\text{sg}$ will maintain the same output, but its gradient is forced to zero. Thus, for $z_q$ in Equation (2), we have

In this way, what’s fed into the decoder is still the quantized $e_k$, but the optimizer uses $z$ when calculating gradients. Since $z$ comes from the encoder, the encoder can also be optimized. This operation is called “Straight-Through Estimator (STE),” and it’s one of the common techniques for designing gradients for non-differentiable modules in neural networks.

Since gradient-based optimizers are still the mainstream, directly designing gradients is often closer to the essence than designing losses, and naturally, it’s usually more challenging and genuinely admirable.

Loss

#

However, the story isn’t over yet; there are two issues. 1. The encoder now has gradients, but the codebook $e_1,e_2,\cdots,e_K$ does not. 2. While $\text{sg}$ allows for arbitrary gradient definition, not just any definition will successfully optimize the model. From Equation (3), we can see that for it to be mathematically strictly true, the unique solution is $e_k=z$. This tells us that if STE is reasonable, then $e_k$ and $z$ must at least be similar. Therefore, for gradient rationality and to optimize the codebook, we can add an auxiliary loss term:

This term simultaneously forces $e_k$ to be close to $z$ and gives $e_k$ gradients, killing two birds with one stone! However, upon closer inspection, there’s a slight imperfection: theoretically, the reconstruction loss of the encoder and decoder is already sufficient to optimize $z$, so the additionally introduced term should primarily be used to optimize $e_k$, and not significantly affect $z$ in return. To address this, we again utilize the $\text{sg}$ trick, and it’s not hard to prove that the gradient of Equation (4) is equivalent to:

The first term stops the gradient of $z$, leaving only the gradient of $e_k$, while the second term does the opposite. Currently, the two terms are summed with $1:1$ weights, meaning they influence each other to the same extent. However, as we just stated, this auxiliary loss should primarily optimize $e_k$ rather than $z$. Therefore, we introduce $\beta > \gamma > 0$ and change the auxiliary loss to:

Then, by adding it to the reconstruction loss, we obtain the total VQ-VAE loss.

Besides, there’s another approach for optimizing $e_k$: first, set $\beta$ in Equation (5) to zero, which again removes gradients from $e_k$. Then, we observe that VQ-VAE’s VQ operation is somewhat similar to K-Means clustering, where $e_1,e_2,\cdots,e_K$ are analogous to $K$ cluster centers. Based on our understanding of K-Means, a cluster center is the average of all vectors in that class. Therefore, one optimization method for $e_k$ is the moving average of $z$:

This is equivalent to specifically using SGD to optimize the $\Vert e_k - \text{sg}[z]\Vert^2$ loss term (other terms can use Adam, etc.). This approach is used by VQ-VAE-2.

FSQ

#

Some readers might wonder, isn’t the topic of this article FSQ? Haven’t I spent a bit too much space introducing VQ-VAE? In fact, because FSQ fully lives up to the “embarrassingly simple” description, introducing FSQ only requires “a few lines” compared to VQ-VAE. So, if VQ-VAE wasn’t described in detail, this blog post wouldn’t have many words~ Of course, by detailing VQ-VAE, everyone can appreciate the simplicity of FSQ even more deeply.

To be precise, FSQ is only used to replace the “VQ” in VQ-VAE. Its discretization idea is very, very simple: “rounding.” First, assume we have a scalar $t\in\mathbb{R}$, we define:

Here, $L\in\mathbb{N}$ is a hyperparameter, $\sigma(x)=1/(1+e^{-x})$ is the sigmoid function (the original paper used $\tanh$, but I believe sigmoid is more scientifically sound), and $\text{Round}$ refers to rounding to the nearest integer. Thus, it’s easy to see that $\text{FSQ}(t)\in\{0,1,\cdots,L-1\}$, meaning the FSQ operation limits the output to $L$ integers, thereby achieving discretization. Of course, in most cases, a single scalar isn’t enough. For $z\in\mathbb{R}^d$, each dimension can undergo the FSQ operation, leading to:

That is, the $d$-dimensional vector $z$ is discretized into one of $L^d$ integers. However, it’s important to note that the $\text{Round}$ operation also has no gradient (or a zero gradient). But, having laid the groundwork with VQ-VAE, some readers might have already guessed what comes next: again, utilizing the STE trick:

That is, for backpropagation, the gradient is computed using $(L-1)\sigma(z)$ before the $\text{Round}$ operation. Since the values before and after $\text{Round}$ are numerically approximate, FSQ does not require an additional loss to enforce this approximation, nor does it need an extra codebook to update. The simplicity of FSQ is thus evident!

Experiments

#

If VQ is understood as directly clustering encoding vectors into $K$ distinct categories, then FSQ is about deriving $d$ attributes from the encoding vectors, with each attribute divided into $L$ levels, thereby directly representing $L^d$ distinct integers. Of course, from a most general perspective, the number of levels for each attribute could also be different, say $L_1,L_2,\cdots,L_d$, leading to $L_1 L_2\cdots L_d$ different combinations.

According to the original paper’s suggestion, $L\geq 5$ (whereas the previous LFQ is equivalent to $L=2$). So, if we want to align with VQ-VAE’s number of codes $K$, for FSQ, we should have $d = \log_L K$. This means FSQ imposes restrictions on the dimension $d$ of the encoding vector (typically a single digit) and it is usually much smaller than VQ-VAE’s encoding dimension (typically three digits). The direct consequence is that when the total number of codes $K$ is relatively small (and thus $d$ is also small), FSQ’s performance is usually inferior to VQ:

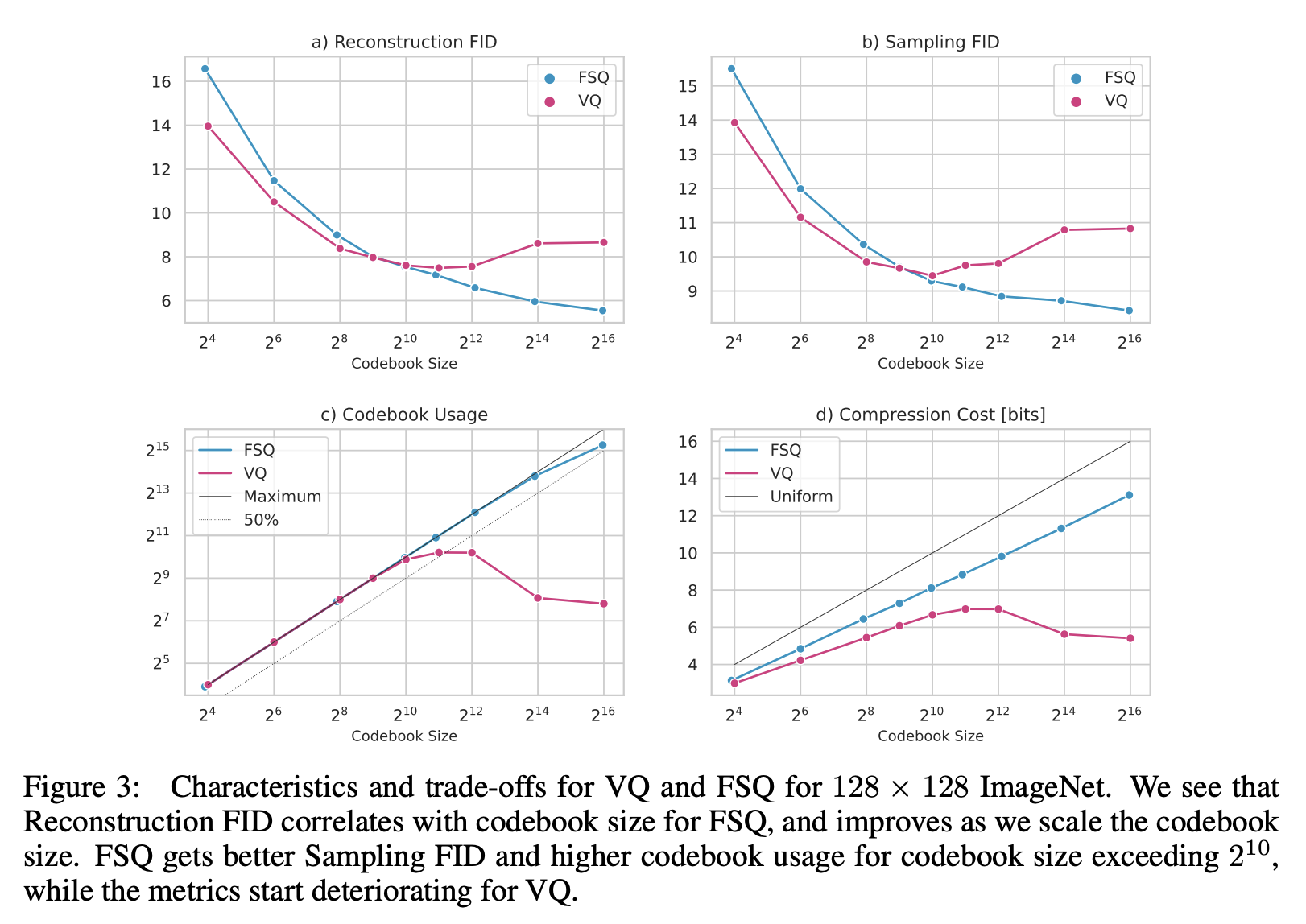
Github: https://github.com/bojone/FSQ

Other experiments are conventional task experiments demonstrating FSQ’s superiority over VQ, which readers can find in the original paper.

Summary (formatted)

#

This article introduced a very simple replacement for VQ-VAE’s “VQ”—FSQ (Finite Scalar Quantization). It directly discretizes continuous vectors through rounding and does not require additional loss terms for assistance. Experimental results indicate that FSQ offers advantages over VQ when the codebook is sufficiently large.

@online{kexuefm-9826,
        title={An Embarrassingly Simple FSQ: "Rounding" Surpasses VQ-VAE},
        author={苏剑林},
        year={2023},
        month={10},
        url={\url{https://kexue.fm/archives/9826}},
}