17. Simple Thoughts on Multimodal Positional Encoding

In the second article of this series, “The Transformer Evolution: 2. Rotary Positional Encoding that Absorbs Strengths”, the author proposed Rotary Positional Encoding (RoPE) - a scheme that achieves relative positional encoding in the form of absolute positions. Initially, RoPE was designed for one-dimensional sequences like text and audio (RoPE-1D). Later, in “The Transformer Evolution: 4. Two-Dimensional Rotary Positional Encoding”, we extended it to two-dimensional sequences (RoPE-2D), which is suitable for image ViTs. However, whether it’s RoPE-1D or RoPE-2D, their common characteristic is a single modality, i.e., pure text or pure image input scenarios. So, for multimodal scenarios like text-image mixture inputs, how should RoPE be adjusted?

I searched around and found little work discussing this issue. The mainstream approach seems to be directly flattening all inputs and treating them as one-dimensional inputs to apply RoPE-1D, thus even RoPE-2D is rarely seen. Leaving aside whether this approach might become a bottleneck for performance when image resolution is further increased, it ultimately feels inelegant. Therefore, next, we attempt to explore a natural combination of the two.

Rotary Position
#

The word “Rotary” in the name RoPE comes from the rotation matrix $\boldsymbol{\mathcal{R}}_n=\begin{pmatrix}\cos n\theta & -\sin n\theta\\ \sin n\theta & \cos n\theta\end{pmatrix}$, which satisfies

$$ \boldsymbol{\mathcal{R}}_m^{\top}\boldsymbol{\mathcal{R}}_n=\boldsymbol{\mathcal{R}}_{n-m} $$

This allows the inner product of $\boldsymbol{q},\boldsymbol{k}$ (assuming they are column vectors) to be

$$ \left(\boldsymbol{\mathcal{R}}_m\boldsymbol{q}\right)^{\top} \left(\boldsymbol{\mathcal{R}}_n\boldsymbol{k}\right)= \boldsymbol{q}^{\top}\boldsymbol{\mathcal{R}}_m^{\top}\boldsymbol{\mathcal{R}}_n \boldsymbol{k}=\boldsymbol{q}^{\top}\boldsymbol{\mathcal{R}}_{n-m}\boldsymbol{k} $$

In the leftmost expression, $\boldsymbol{\mathcal{R}}_m\boldsymbol{q},\boldsymbol{\mathcal{R}}_n\boldsymbol{k}$ are computed independently, without involving the interaction of $m,n$, so formally it is an absolute position. However, the equivalent form on the far right only depends on the relative position $n-m$, so when combined with Dot-Product Attention, it effectively behaves as a relative position. This characteristic also gives RoPE translational invariance: since $(n+c) - (m+c) = n-m$, if a constant is added to all absolute positions before applying RoPE, the Attention result should theoretically not change (in practice, due to computational precision limitations, there may be tiny errors).

The above is for $\boldsymbol{q},\boldsymbol{k}\in\mathbb{R}^2$. For $\boldsymbol{q},\boldsymbol{k}\in \mathbb{R}^d$ (where $d$ is an even number), we need a $d\times d$ rotation matrix. For this, we introduce $d/2$ different $\theta$ values and construct a block-diagonal matrix

$$ \small{\boldsymbol{\mathcal{R}}_n^{(d\times d)} = \begin{pmatrix} \cos n\theta_0 & -\sin n\theta_0 & 0 & 0 & \cdots & 0 & 0 \\ \sin n\theta_0 & \cos n\theta_0 & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & \cos n\theta_1 & -\sin n\theta_1 & \cdots & 0 & 0 \\ 0 & 0 & \sin n\theta_1 & \cos n\theta_1 & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & \cos n\theta_{d/2-1} & -\sin n\theta_{d/2-1} \\ 0 & 0 & 0 & 0 & \cdots & \sin n\theta_{d/2-1} & \cos n\theta_{d/2-1} \\ \end{pmatrix}} $$

From an implementation perspective, this involves grouping $\boldsymbol{q},\boldsymbol{k}$ in pairs, applying a 2D rotation transformation with a different $\theta$ for each group, and then combining them. This is existing RoPE content and will not be elaborated further. In principle, we only need to find a solution for the lowest dimension, which can then be generalized to arbitrary dimensions through block-diagonal construction. Therefore, the following analysis will only consider the minimum dimension.

Two-Dimensional Position
#

When we talk about the concept of “dimension”, it can have multiple meanings. For example, we just said $\boldsymbol{q},\boldsymbol{k}\in \mathbb{R}^d$, which means $\boldsymbol{q},\boldsymbol{k}$ are $d$-dimensional vectors. However, the RoPE-1D and RoPE-2D focused on in this article do not refer to this dimension, but rather the dimension needed to record a position.

Text and its Position IDs

For instance, to represent the position of a token in text, we only need a scalar $n$, indicating it is the $n$-th token. But for images, even after patchification, they usually retain width and height dimensions. So we need a pair of coordinates $(x,y)$ to accurately encode the position of a patch:

Image and its Position Coordinates

The previous section introduced $\boldsymbol{\mathcal{R}}_n$, which only encodes a scalar $n$, so it is RoPE-1D. To handle image input more reasonably, we need to extend it to the corresponding RoPE-2D:

$$ \boldsymbol{\mathcal{R}}_{x,y}=\left( \begin{array}{cc:cc} \cos x\theta & -\sin x\theta & 0 & 0 \\ \sin x\theta & \cos x\theta & 0 & 0 \\ \hdashline 0 & 0 & \cos y\theta & -\sin y\theta \\ 0 & 0 & \sin y\theta & \cos y\theta \\ \end{array}\right) = \begin{pmatrix}\boldsymbol{\mathcal{R}_x} & 0 \\ 0 & \boldsymbol{\mathcal{R}_y}\end{pmatrix} $$

Clearly, this is just a block-diagonal combination of $\boldsymbol{\mathcal{R}}_x$ and $\boldsymbol{\mathcal{R}}_y$, and thus it can naturally be extended to 3D or even higher dimensions. From an implementation perspective, it becomes simpler: it splits $\boldsymbol{q},\boldsymbol{k}$ into two halves (three equal parts for 3D, four for 4D, and so on), each half being a vector in $\mathbb{R}^{d/2}$, and then one half undergoes RoPE-1D for $x$, and the other half undergoes RoPE-1D for $y$, finally combining them.

It should be noted that, for symmetry and simplicity, the $\boldsymbol{\mathcal{R}}_{x,y}$ constructed above uses the same $\theta$ for $x,y$. However, this is not strictly necessary in principle; under appropriate circumstances, we can configure slightly different $\theta$ values for $x$ and $y$ separately.

Forced Dimensionality Reduction
#

Now we see that the position of text is a scalar $n$, while the position of an image is a vector $(x,y)$. The two are inconsistent, which requires some techniques to reconcile the inconsistency when processing text-image mixed inputs.

The most direct approach, as mentioned at the beginning of the article, is to directly flatten the image into a one-dimensional vector sequence and then treat it as ordinary text. It gets positional encoding the same way text does. This approach is naturally very general and not limited to adding RoPE; any absolute positional encoding can be added. I estimate that some existing multimodal models, such as Fuyu-8b, Deepseek-VL, Emu2, etc., do this, perhaps with some subtle differences in handling, such as potentially adding a special token representing [SEP] to separate patches from different rows:

Text and Images Both Flattened to One Dimension for Processing

This approach also aligns with the current mainstream Decoder-Only architecture, because Decoder-Only means that even without positional encoding, it is not permutation invariant, so we must manually specify the input order that we deem best. And since the input order is specified, using one-dimensional positional encoding according to the specified order is a very natural choice. Furthermore, in the case of pure text, the model following this approach is no different from a regular pure text LLM, which also allows us to continue training a multimodal model from a pre-trained text LLM.

However, from my perspective, the concept of positional encoding itself should not be tied to the usage of Attention; it should be applicable to Decoder, Encoder, and even arbitrary Attention Masks. On the other hand, preserving the two-dimensionality of position can maximize the retention of our prior knowledge about nearby positions. For example, we believe that positions $(x+1,y)$ and $(x,y+1)$ should both have a distance similar to $(x,y)$. But if flattened (first horizontally, then vertically), $(x,y)$ becomes $xw + y$, while $(x+1,y)$ and $(x,y+1)$ become $xw+y+w$ and $xw+y+1$ respectively. The distance between the former and $xw + y$ depends on $w$, while the latter is a fixed $1$. Of course, we can specify other orders, but no matter how the order is specified, it is impossible to fully accommodate the proximity of all neighboring positions, because one dimension is missing, significantly reducing the expressiveness of similarity.

Unified Dimensionality Elevation
#

From a vector space perspective, a one-dimensional scalar can be seen as a special two-dimensional vector. Therefore, compared to flattening to one dimension, if we instead unify the positions of all inputs to two dimensions, there is in principle more operational space.

For this purpose, we can consider a common layout method: using images as separators to segment text. Consecutive text is treated as a single line, while an image is treated as multiple lines of text. Then the entire text-image mixed input is equivalent to a long multi-line document, where each text token or image patch has its own row number $x$ and its order $y$ within the line. This assigns a two-dimensional position $(x,y)$ to all input units (tokens or patches), allowing us to uniformly encode positions using RoPE-2D (other 2D forms of positional encoding are also theoretically possible) while preserving the original two-dimensionality of image positions.

Simulating Layout to Uniformly Construct 2D Position Coordinates

Clearly, the main advantage of this approach is that it is very intuitive, directly corresponding to the actual visual layout, which is easy to understand and generalize. But it also has a very obvious disadvantage, which is that for pure text input, it cannot degenerate to RoPE-1D, but instead becomes RoPE-2D where $x$ is always 1. This makes the feasibility of training a multimodal LLM starting from an already trained text LLM questionable. Furthermore, using images as segmentation points means that when there are many images, the text might be segmented too “fragmented,” specifically including large fluctuations in the length of each text segment and forcibly breaking lines for text that should be continuous. These could become bottlenecks limiting performance.

Combining into One
#

If we want to preserve the position information of image patches without loss, unifying to two dimensions and using RoPE-2D (or other 2D forms of positional encoding) seems to be the necessary choice. So the scheme in the previous section is already on the right track. We need to further consider how to make it degenerate to RoPE-1D for pure text input, to be compatible with existing text LLMs.

First, we already mentioned that $\boldsymbol{\mathcal{R}}_{x,y}$ is a block-diagonal combination of $\boldsymbol{\mathcal{R}}_x$ and $\boldsymbol{\mathcal{R}}_y$. Therefore, $\boldsymbol{\mathcal{R}}_{n,n}$ is a block-diagonal combination of two $\boldsymbol{\mathcal{R}}_n$. RoPE-1D’s $\boldsymbol{\mathcal{R}}_n^{(d\times d)}$ is also a block-diagonal combination of multiple $\boldsymbol{\mathcal{R}}_n$ with different $\theta$. Thus, as long as we select different $\theta$ values from $\boldsymbol{\mathcal{R}}_n^{(d\times d)}$ for $x$ and $y$, $\boldsymbol{\mathcal{R}}_{n,n}$ can be seen as part of RoPE-1D (i.e., $\boldsymbol{\mathcal{R}}_n^{(d\times d)}$). From this perspective, for RoPE-2D to degenerate to RoPE-1D, the position of text should take the form of $(n,n)$, rather than using other methods to specify a row number as in the previous section.

Then, within the image, we use regular RoPE-2D. For a single image with $w\times h$ patches, its two-dimensional position coordinates when flattened are

$$ \begin{array}{c|cccc|cccc|c|cccc} \hline x & 1 & 1 & \cdots & 1 & 2 & 2 & \cdots & 2 & \quad \cdots \quad & h & h & \cdots & h \\ \hline y & 1 & 2 & \cdots & w & 1 & 2 & \cdots & w & \quad \cdots \quad & 1 & 2 & \cdots & w \\ \hline \end{array} $$

If this image is placed after a sentence of length $L$, the position encoding of the last token in this sentence is $(L,L)$. Thus, the position encoding of the image following the sentence should look like

$$ \begin{array}{c|cccc|c|cccc} \hline x & L+1 & L+1 & \cdots & L+1 & \quad \cdots \quad & L+h & L+h & \cdots & L+h \\ \hline y & L+1 & L+2 & \cdots & L+w & \quad \cdots \quad & L+1 & L+2 & \cdots & L+w \\ \hline \end{array} $$

But this is not perfect, because the position of the last token of the sentence is $(L,L)$, and the position of the first patch of the image is $(L+1,L+1)$, their difference is $(1,1)$. Suppose another sentence follows this image. Let the position of the first token of that sentence be $(K,K)$, and the position of the last patch of the image be $(L+h,L+w)$. When $w\neq h$, no matter how we set $K$, it’s impossible for the difference between $(K,K)$ and $(L+h,L+w)$ to be $(1,1)$, meaning there is asymmetry regarding the sentences on the left and right of the image. This feels inelegant.

To improve this, we can multiply the $x,y$ coordinates of the image by positive numbers $s,t$ respectively:

$$ \begin{array}{c|cccc|cccc|c|cccc} \hline x & s & s & \cdots & s & 2s & 2s & \cdots & 2s & \quad \cdots \quad & hs & hs & \cdots & hs \\ \hline y & t & 2t & \cdots & wt & t & 2t & \cdots & wt & \quad \cdots \quad & t & 2t & \cdots & wt \\ \hline \end{array} $$

As long as $s,t\neq 0$, this scaling does not lose position information, so such an operation is allowed. With the introduction of scaling, assuming the position of the last token of the sentence is still $(L,L)$, the image positions are also the sequence above plus $L$. At this point, the difference between “the position of the last token of the sentence” and “the position of the first patch of the image” is $(s,t)$. If we hope that the difference between “the position of the first token of the sentence after the image” and “the position of the last patch of the image” is also $(s,t)$, then we should have

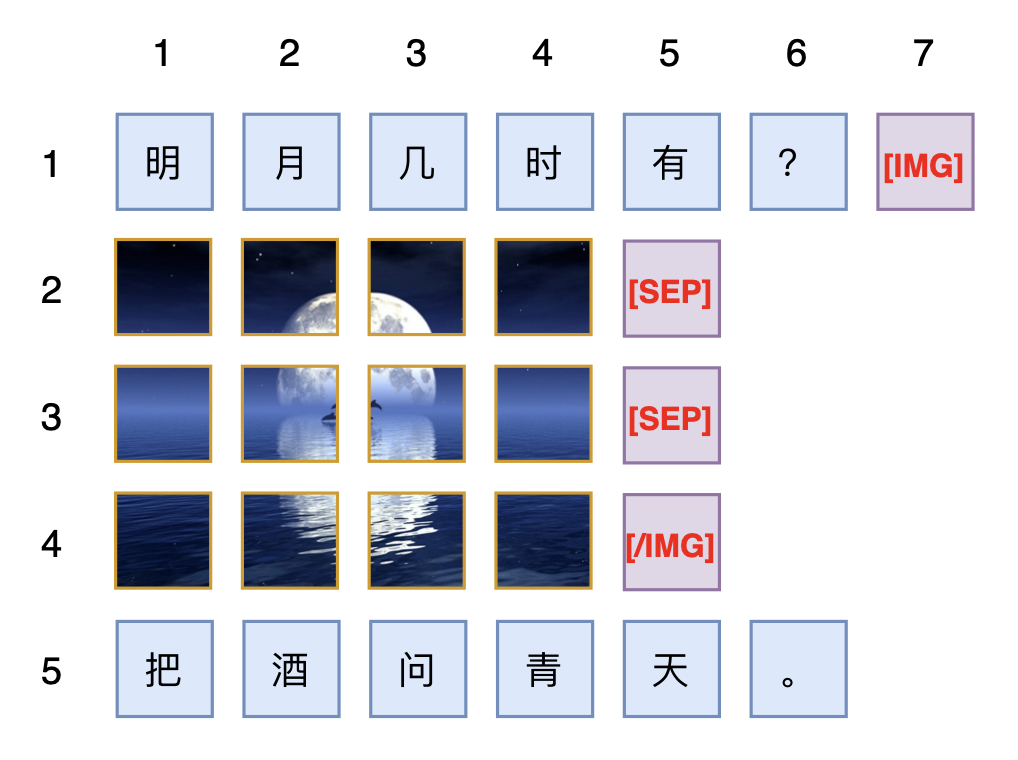
$$ \begin{pmatrix}L + hs \\ L + wt \end{pmatrix} + \begin{pmatrix}s \\ t \end{pmatrix} = \begin{pmatrix}K \\ K \end{pmatrix}\quad \Rightarrow \quad (h+1)s = (w+1)t $$

Considering the arbitrary nature of $h,w$, and hoping to ensure all position IDs are integers, the simplest solution is naturally $s=w+1,t=h+1$, and the position of the first token of the new sentence will be $K=L+(w+1)(h+1)$. A specific example is shown in the figure below:

2D Position Supporting Degeneration to RoPE-1D

Further Thoughts
#

The position of the last token of the left sentence is $L$, and the position of the first token of the right sentence is $K=L+(w+1)(h+1)$. If the middle part were also a sentence, then it could be inferred that this sentence has $(w+1)(h+1)-1$ tokens. This is equivalent to saying that if a $w\times h$ image is sandwiched between two sentences, the relative position between these two sentences is equivalent to being separated by a sentence of $(w+1)(h+1)-1$ tokens. This number looks a bit unnatural, because $wh$ seems like the perfect answer, but unfortunately, this is the simplest solution that guarantees all position IDs are integers. If non-integer position IDs are allowed, then it can be agreed that a $w\times h$ image is equivalent to $wh$ tokens, which in turn leads to

$$ s = \frac{wh + 1}{h+1}, \quad t = \frac{wh + 1}{w+1} $$

Some readers might ask: if two images of different sizes are adjacent, is there no such symmetrical scheme? This is not difficult. We just need to add special tokens before and after each image, such as [IMG] and [/IMG], and encode these special tokens’ positions as if they were ordinary text tokens. This directly avoids the situation where two images are directly adjacent (because by convention, patches of the same image must be sandwiched between [IMG] and [/IMG], and these two tokens are treated as text, so it’s equivalent to saying that each image is necessarily sandwiched between two text segments). Furthermore, [SEP] was not mentioned in the above discussion. If needed, it can be introduced manually. In fact, [SEP] is only necessary when doing image generation using patch by patch autoregressive methods. If images are purely used as input, or if image generation is done using diffusion models, then [SEP] is redundant.

Thus far, our derivation on extending RoPE to text-image mixed inputs is complete. If a name is needed, the final scheme can be called “RoPE-Tie (RoPE for Text-image)”. It must be said that the final RoPE-Tie is not particularly elegant, to the extent that it gives a feeling of being “ornate”. In terms of effectiveness, compared to directly flattening to one dimension and using RoPE-1D, using RoPE-Tie is not guaranteed to provide any improvement; it is more a product of the author’s “compulsive disorder”. Therefore, for multimodal models that have already scaled to a certain size, there is no need to make any changes. However, if you haven’t started or are just starting, you might consider trying RoPE-Tie.

Summary (formatted)
#

This article discussed how to combine RoPE-1D and RoPE-2D to better handle text-image mixed input formats. The main idea is to support the two-dimensional position indicators of images through RoPE-2D, and by applying appropriate constraints, ensure that it can degenerate to the conventional RoPE-1D in the case of pure text.

@online{kexuefm-10040,
        title={The Transformer Evolution: 17. Simple Thoughts on Multimodal Positional Encoding},
        author={苏剑林},
        year={2024},
        month={03},
        url={\url{https://kexue.fm/archives/10040}},
}