1. Tracing the Origins of Sinusoidal Position Encoding

Recently, I’ve made some attempts to understand and improve the Transformer, gaining some seemingly valuable experience and conclusions. Therefore, I am starting a series to summarize them, titled “The Road to Transformer Improvement,” representing both a deeper understanding and resulting improvements.

As the first article in this series, I will introduce my new understanding of the Sinusoidal position encoding proposed by Google in 《Attention is All You Need》:

where $\boldsymbol{p}_{k,2i}, \boldsymbol{p}_{k,2i+1}$ are the $2i$-th and $(2i+1)$-th components of the encoding vector for position $k$, and $d$ is the vector dimension.

As an explicit solution for position encoding, Google provided very little description of it in the original paper, merely mentioning that it can express relative position information. Later, some interpretations appeared on platforms like Zhihu, and some of its characteristics gradually became known, but overall, they are scattered. Especially for fundamental questions like “How was it conceived?” or “Does it have to be in this form?”, there are no satisfactory answers yet.

Therefore, this article primarily focuses on pondering these questions. Perhaps, during the thinking process, readers will share my feeling: the more you think about this design, the more ingenious and beautiful you realize it is, truly awe-inspiring.

Taylor Expansion

#

Suppose our model is $f(\cdots,\boldsymbol{x}_m,\cdots,\boldsymbol{x}_n,\cdots)$, where $\boldsymbol{x}_m, \boldsymbol{x}_n$ denote the $m$-th and $n$-th inputs, respectively. Without loss of generality, let $f$ be a scalar function. For a pure Attention model without an Attention Mask, it is fully symmetric, meaning for any $m, n$, we have

This is why we say Transformer cannot identify position—due to full symmetry. Simply put, the function naturally satisfies the identity $f(x,y)=f(y,x)$, making it impossible to distinguish from the output whether the input sequence was $[x,y]$ or $[y,x]$.

Therefore, what we need to do is break this symmetry, for instance, by adding a different encoding vector at each position:

Generally, as long as the encoding vector is different for each position, this full symmetry is broken, and $\tilde{f}$ can be used instead of $f$ to process ordered inputs. But now we hope to further analyze the properties of position encoding and even obtain an explicit solution, so we cannot stop here.

To simplify the problem, let’s consider only the position encodings at positions $m, n$, treating them as perturbation terms, and perform a Taylor expansion up to the second order:

As we can see, the first term is independent of position. Terms 2 through 5 depend only on a single position, so they represent pure absolute position information. The 6th term is the first interaction term involving both $\boldsymbol{p}_m$ and $\boldsymbol{p}_n$. We denote it as $\boldsymbol{p}_m^{\top} \boldsymbol{\mathcal{H}} \boldsymbol{p}_n$ and hope it can express some relative position information.

(The Taylor expansion here references the answer by Nanami-chan on the Zhihu question 《BERT为何使用学习的position embedding而非正弦position encoding?》.)

Relative Position

#

Let’s start with a simple example. Assume $\boldsymbol{\mathcal{H}}=\boldsymbol{I}$ is the identity matrix. In this case, $\boldsymbol{p}_m^{\top} \boldsymbol{\mathcal{H}} \boldsymbol{p}_n = \boldsymbol{p}_m^{\top} \boldsymbol{p}_n = \langle\boldsymbol{p}_m, \boldsymbol{p}_n\rangle$ is the dot product of the two position encodings. We hope that in this simple example, this term expresses relative position information, meaning there exists some function $g$ such that

Here, $\boldsymbol{p}_m, \boldsymbol{p}_n$ are $d$-dimensional vectors. Let’s start with the simplest case, $d=2$.

For 2-dimensional vectors, we can use complex numbers for derivation, treating the vector $[x,y]$ as a complex number $x + y\text{i}$. According to the rules of complex multiplication, we can easily get:

where $\boldsymbol{p}_n^*$ is the complex conjugate of $\boldsymbol{p}_n$, and $\text{Re}[]$ denotes the real part of the complex number. To satisfy the equation $\langle\boldsymbol{p}_m, \boldsymbol{p}_n\rangle = g(m-n)$, we can assume there exists a complex number $\boldsymbol{q}_{m-n}$ such that

Taking the real part of both sides then gives the equation. To solve this equation, we can use the exponential form of complex numbers. Let $\boldsymbol{p}_m=r_m e^{\text{i}\phi_m}, \boldsymbol{p}_n^*=r_n e^{-\text{i}\phi_n}, \boldsymbol{q}_{m-n}=R_{m-n} e^{\text{i}\Phi_{m-n}}$ to get

For the first equation, substituting $n=m$ gives $r_m^2=R_0$, meaning $r_m$ is a constant. For simplicity, let’s set it to 1. For the second equation, substituting $n=0$ gives $\phi_m - \phi_0=\Phi_m$. For simplicity, let’s set $\phi_0=0$, then $\phi_m=\Phi_m$. Thus, $\phi_m - \phi_n=\phi_{m-n}$. Substituting $n=m-1$ gives $\phi_m - \phi_{m-1}=\phi_1$, meaning $\{\phi_m\}$ is just an arithmetic progression with the general solution $m\theta$. Therefore, we get the solution for the position encoding in the 2D case:

Since the dot product satisfies linear superposition, higher-dimensional even-dimensional position encodings can be represented as a combination of multiple 2D position encodings:

This also satisfies the equation $\langle\boldsymbol{p}_m, \boldsymbol{p}_n\rangle = g(m-n)$. Of course, this can only be called a solution to the equation, not the unique solution. For us, finding a simple solution is sufficient.

Long-Range Decay

#

Based on the previous assumptions, we derived the form of position encoding $\boldsymbol{p}_m=\begin{pmatrix}\cos m\theta_0 \\ \sin m\theta_0 \\ \dots \\ \sin m\theta_{d/2-1} \end{pmatrix}$, which is essentially the same form as the standard Sinusoidal position encoding, differing only in the positions of $\sin$ and $\cos$. Generally, neurons in a neural network are unordered, so even permuting the dimensions is a valid position encoding. Thus, apart from the undetermined $\theta_i$, the derived form and the standard Sinusoidal form are fundamentally the same.

The choice in the standard form is $\theta_i = 10000^{-2i/d}$. What is the significance of this choice? In fact, this form has a nice property: it causes $\langle\boldsymbol{p}_m, \boldsymbol{p}_n\rangle$ to tend towards zero as $|m-n|$ increases. According to our intuition, the correlation between inputs with greater relative distance should be weaker, so this property aligns with our intuition. However, how can periodic trigonometric functions exhibit a decay trend?

This is indeed a magical phenomenon, originating from the asymptotic decay of high-frequency oscillatory integrals. Specifically, we write the dot product as

Thus, the problem becomes one of estimating the asymptotics of the integral $\int_0^1 e^{\text{i}(m-n)\theta_t}dt$. In fact, the estimation of such oscillatory integrals is common in quantum mechanics, and methods from there can be used for analysis. However, for us, the most direct method is to plot the result of the integral using Mathematica:

\[Theta][t_] = (1/10000)^t;
f[x_] = Re[Integrate[Exp[I*x*\[Theta][t]], {t, 0, 1}]];
Plot[f[x], {x, -128, 128}]

And from the image, we can see that it indeed exhibits a decay trend:

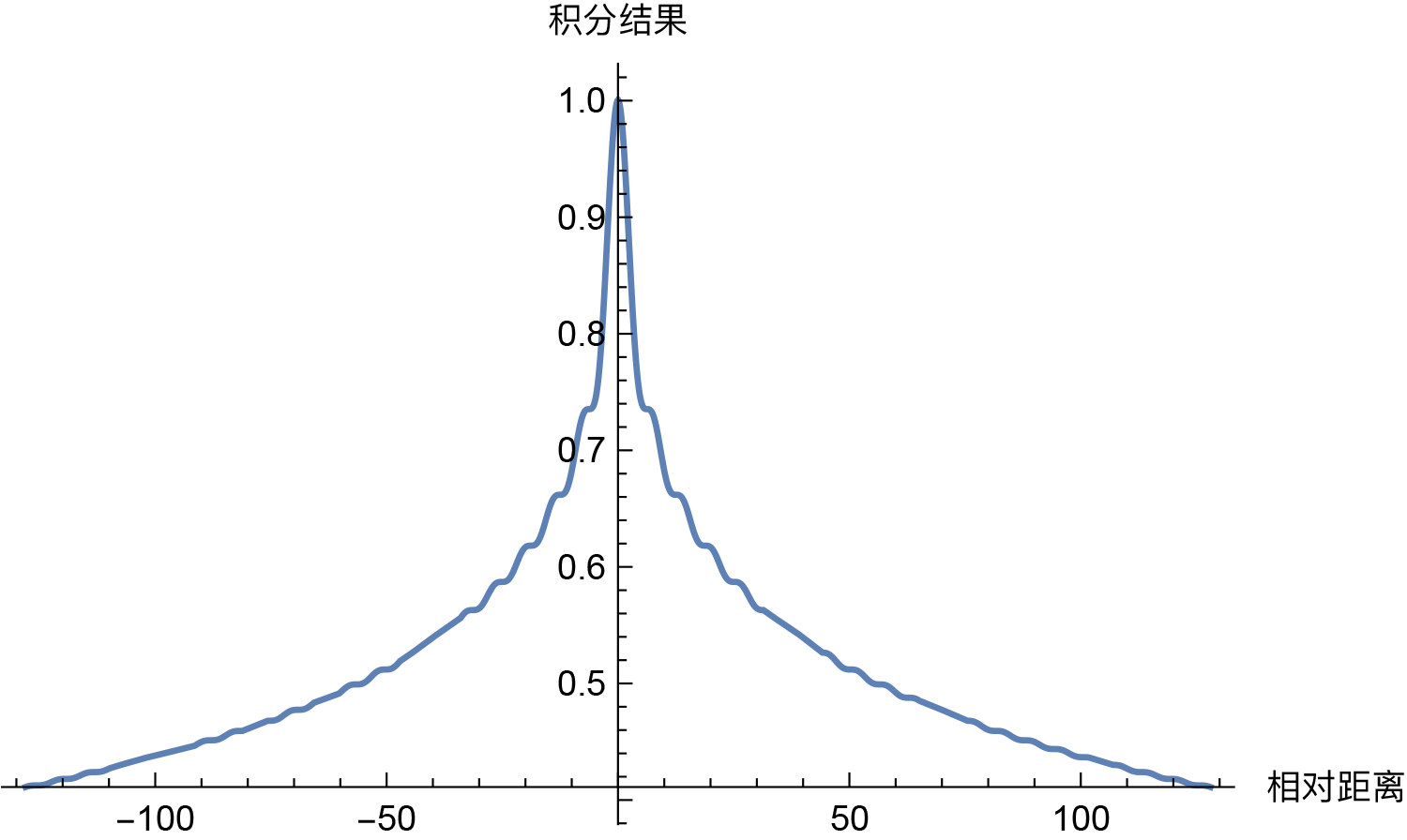
So, the question arises: must it be $\theta_t = 10000^{-t}$ to show a long-range decay trend? Of course not. In fact, for our scenario, “almost” any monotonic smooth function $\theta_t$ on $[0,1]$ can make the integral $\int_0^1 e^{\text{i}(m-n)\theta_t}dt$ have an asymptotic decay trend, such as the power function $\theta_t = t^{\alpha}$. So, is there anything special about $\theta_t = 10000^{-t}$? Let’s compare some results.

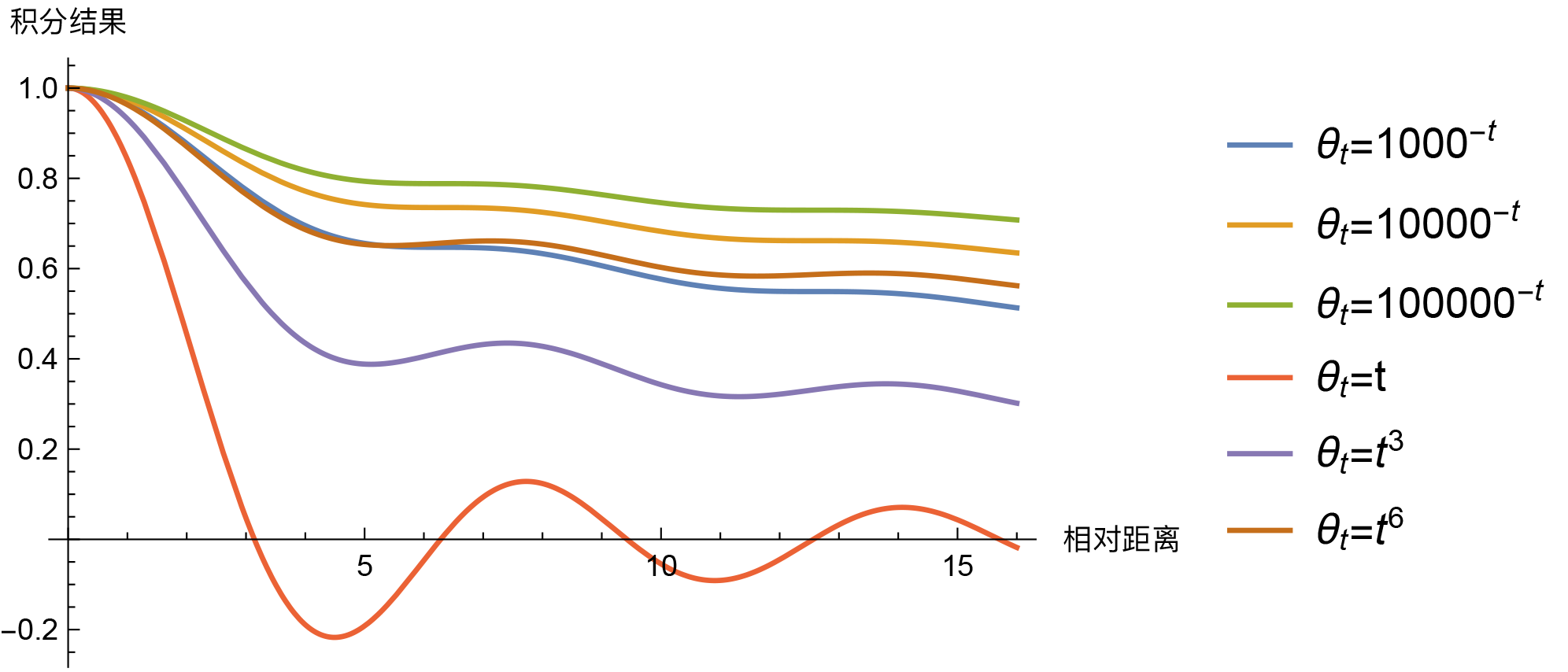
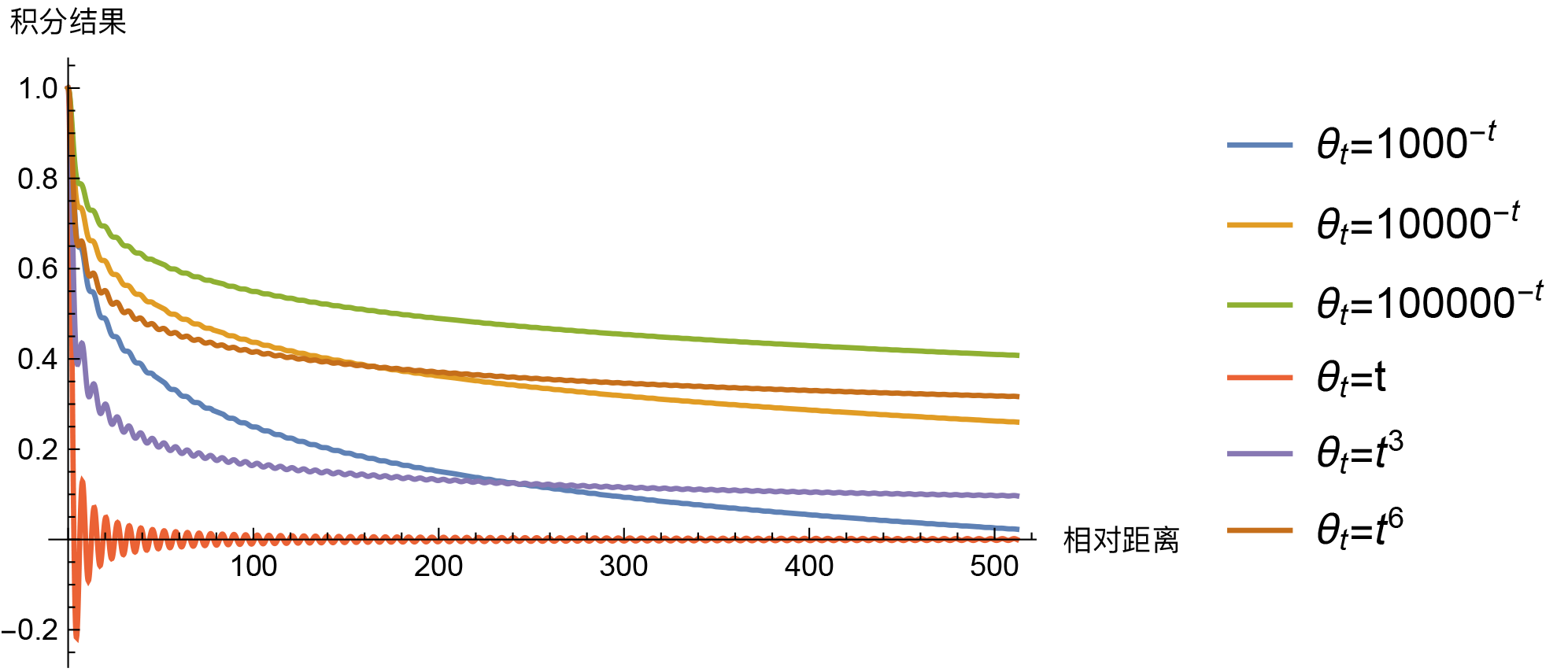
Looking at them this way, besides $\theta_t=t$ being somewhat abnormal (having intersection points with the horizontal axis), there isn’t much obvious distinction between the others. It’s hard to tell which is superior. Power functions decay a bit faster at short distances, while exponential functions decay a bit faster at long distances. The closer $\theta_t$ is to 0 overall, the slower the overall decay, and so on. From this perspective, $\theta_t = 10000^{-t}$ is just a compromise choice, with no particular specialness. If I were to choose, I would likely pick $\theta_t = 1000^{-t}$. Another option is to directly set $\theta_i = 10000^{-2i/d}$ as the initialization values for each $\theta_i$, and then make them trainable, allowing the model to automatically finetune them. This way, there’s no need to dwell on which one to choose.

General Case

#

In the previous two sections, we showed the idea of expressing relative position information through absolute position encoding, and with the constraint of long-range decay, we could “deduce” the Sinusoidal position encoding, and also suggested other choices for $\theta_i$. But let’s not forget, up to now, our derivation has been based on the simple case $\boldsymbol{\mathcal{H}}=\boldsymbol{I}$. For a general $\boldsymbol{\mathcal{H}}$, would the aforementioned Sinusoidal position encoding still possess these good properties?

If $\boldsymbol{\mathcal{H}}$ is a diagonal matrix, then some of the above properties can be retained. In this case,

Using product-to-sum formulas, we get

We can see that it indeed contains the relative position $m-n$, but it might also have the $m+n$ term. If this term is not needed, the model can make $\boldsymbol{\mathcal{H}}_{2i,2i} = \boldsymbol{\mathcal{H}}_{2i+1,2i+1}$ to eliminate it. In this special case, we point out that Sinusoidal position encoding provides the model with the possibility of learning relative positions. As for what specific position information is needed, it is determined by the model’s training itself.

Notably, for the above expression, the long-range decay property still exists. For example, for the first summation term, analogous to the approximation in the previous section, it is equivalent to the integral

Similarly, some estimation results for oscillatory integrals (refer to 《Oscillatory integrals》, 《学习笔记3-一维振荡积分与应用》, etc.) tell us that this oscillatory integral tends to zero as $|m-n|\to\infty$ under easily met conditions. Therefore, the long-range decay property can be retained.

If $\boldsymbol{\mathcal{H}}$ is not a diagonal matrix, then unfortunately, it is difficult to reproduce the above properties. We can only hope that the diagonal part of $\boldsymbol{\mathcal{H}}$ is dominant, so that the above properties can be approximately retained. The diagonal part being dominant means that the correlation between any two dimensions of the $d$-dimensional vector is relatively small, satisfying a certain degree of decoupling. For the Embedding layer, this assumption is somewhat reasonable. I have examined the covariance matrix of the word embedding matrix and position embedding matrix trained by BERT and found that the diagonal elements are significantly larger than the off-diagonal elements, proving that the assumption of the diagonal elements being dominant has a certain degree of validity.

Discussion Points

#

Some readers might argue: no matter how much you praise Sinusoidal position encoding, it doesn’t change the fact that directly trained position encoding performs better than Sinusoidal position encoding. Indeed, experiments have shown that in thoroughly pre-trained Transformer models like BERT, directly trained position encoding performs slightly better than Sinusoidal position encoding. This is not denied. What this article attempts to do is merely derive why Sinusoidal position encoding can serve as an effective position encoding based on some principles and assumptions, not to claim that it is necessarily the best position encoding.

The derivation is based on some assumptions. If the derived result is not good enough, it means that the assumptions do not sufficiently match the actual situation. So, for Sinusoidal position encoding, where might the problems lie? We can reflect step by step.

Step 1: Taylor expansion. This relies on $\boldsymbol{p}$ being a small quantity. I have also verified this in BERT and found that the average magnitude of word embeddings is larger than that of position embeddings, indicating that $\boldsymbol{p}$ being small is somewhat reasonable, but it’s hard to say exactly how reasonable because the embedding magnitudes, while larger, are not overwhelmingly so. Step 2: Assuming $\boldsymbol{\mathcal{H}}$ is the identity matrix. As we analyzed in the previous section, it is very likely that the diagonal elements are dominant, so assuming the identity matrix might not be too big of a problem initially. Step 3: Assuming relative position is expressed through the dot product of two absolute position vectors. Intuitively, this should be reasonable; the interaction of absolute positions should have the ability to express some degree of relative position information. The final step: Determining $\theta_i$ through the property of automatic long-range decay. This in itself should be good, but this step introduces too much variability because there are too many possible forms for $\theta_i$, and even trainable $\theta_i$, making it difficult to choose the most reasonable one. Therefore, if Sinusoidal position encoding is not good enough, this step is highly worth reflecting upon.

Summary (formatted)

#

In conclusion, this article attempts to deduce Sinusoidal position encoding based on some assumptions. These assumptions have a certain degree of reasonableness, but also some issues, so the corresponding Sinusoidal position encoding is noteworthy but not flawless. Regardless, in current deep learning, being able to obtain an explicit solution for a specific problem instead of simply relying on brute-force fitting is rare, and Sinusoidal position encoding is such a case, which is worth our contemplation and reflection.

@online{kexuefm-8231,
        title={The Road to Transformer Improvement: 1. Tracing the Origins of Sinusoidal Position Encoding},
        author={苏剑林},
        year={2021},
        month={03},
        url={\url{https://kexue.fm/archives/8231}},
}