gemini-2.5-flash-preview-04-17 translation of a Chinese article. Beware of potential errors.In the previous article, we provided a detailed derivation and understanding of the original Sinusoidal Position Embedding. The overall feeling was that Sinusoidal Position Embedding is a kind of “absolute position embedding that wants to be relative position embedding”. Generally speaking, absolute position embedding has advantages like simple implementation and fast computation, while relative position embedding directly reflects the relative position signal, aligns with our intuitive understanding, and often achieves better actual performance. It is thus evident that if relative position embedding can be implemented using the method of absolute position embedding, it would “gather the strengths of all parties” and “have one’s cake and eat it too”. Sinusoidal Position Embedding vaguely achieved this, but not well enough.
This article will introduce our self-developed Rotary Transformer (RoFormer) model. Its main modification is the application of “Rotary Position Embedding (RoPE)”, conceived by the author. This is a design that, in conjunction with the Attention mechanism, can achieve “implementing relative position embedding using the method of absolute position embedding”. Precisely because of this design, it is currently the only relative position embedding that can be used with linear Attention.
Basic Idea#
We briefly introduced RoPE in a previous article 《Transformer Position Encoding That Makes Researchers Rack Their Brains》, calling it “fusion style” at the time. This article provides a more detailed introduction to its origins and properties. In RoPE, our starting point is “implementing relative position embedding using the method of absolute position embedding”. Doing so has both theoretical elegance and practical utility. For example, its extensibility to linear Attention is primarily due to this point.
To achieve this goal, we assume that absolute position information is added to $\boldsymbol{q}, \boldsymbol{k}$ through the following operations:
$$ \tilde{\boldsymbol{q}}_m = \boldsymbol{f}(\boldsymbol{q}, m), \quad\tilde{\boldsymbol{k}}_n = \boldsymbol{f}(\boldsymbol{k}, n) $$That is to say, we design operations $\boldsymbol{f}(\cdot, m), \boldsymbol{f}(\cdot, n)$ for $\boldsymbol{q}, \boldsymbol{k}$ respectively, such that after this operation, $\tilde{\boldsymbol{q}}_m, \tilde{\boldsymbol{k}}_n$ carry the absolute position information of positions $m, n$. The core operation of Attention is the inner product, so we hope the result of the inner product carries relative position information. Therefore, we assume the following identity holds:
$$ \langle\boldsymbol{f}(\boldsymbol{q}, m), \boldsymbol{f}(\boldsymbol{k}, n)\rangle = g(\boldsymbol{q},\boldsymbol{k},m-n) $$Therefore, we need to find a (as simple as possible) solution to this identity. The solution process also requires some initial conditions. Obviously, we can reasonably set $\boldsymbol{f}(\boldsymbol{q}, 0) = \boldsymbol{q}$ and $\boldsymbol{f}(\boldsymbol{k}, 0) = \boldsymbol{k}$.
Solution Process#
Following the idea from the previous article, we first consider the two-dimensional case, and then use complex numbers to solve it. In complex numbers, we have $\langle\boldsymbol{q}, \boldsymbol{k}\rangle = \text{Re}[\boldsymbol{q}\boldsymbol{k}^*]$, where $\text{Re}[]$ represents the real part of the complex number. Thus, we have
$$ \text{Re}[\boldsymbol{f}(\boldsymbol{q}, m)\boldsymbol{f}^*(\boldsymbol{k}, n)] = g(\boldsymbol{q},\boldsymbol{k},m-n) $$For simplicity, we assume there exists a complex number $\boldsymbol{g}(\boldsymbol{q}, \boldsymbol{k}, m-n)$ such that $\boldsymbol{f}(\boldsymbol{q}, m)\boldsymbol{f}^*(\boldsymbol{k}, n) = \boldsymbol{g}(\boldsymbol{q}, \boldsymbol{k}, m-n)$. Then we use the exponential form of complex numbers, setting
$$ \begin{aligned}\boldsymbol{f}(\boldsymbol{q}, m) =&\, R_f (\boldsymbol{q}, m)e^{\text{i}\Theta_f(\boldsymbol{q}, m)} \\\boldsymbol{f}(\boldsymbol{k}, n) =&\, R_f (\boldsymbol{k}, n)e^{\text{i}\Theta_f(\boldsymbol{k}, n)} \\\boldsymbol{g}(\boldsymbol{q}, \boldsymbol{k}, m-n) =&\, R_g (\boldsymbol{q}, \boldsymbol{k}, m-n)e^{\text{i}\Theta_g(\boldsymbol{q}, \boldsymbol{k}, m-n)} \\\end{aligned} $$Substituting into the equation yields the following system of equations:
$$ \begin{aligned}R_f (\boldsymbol{q}, m) R_f (\boldsymbol{k}, n) =&\, R_g (\boldsymbol{q}, \boldsymbol{k}, m-n) \\\Theta_f (\boldsymbol{q}, m) - \Theta_f (\boldsymbol{k}, n) =&\, \Theta_g (\boldsymbol{q}, \boldsymbol{k}, m-n)\end{aligned} $$For the first equation, substituting $m=n$ gives
$$ R_f (\boldsymbol{q}, m) R_f (\boldsymbol{k}, m) = R_g (\boldsymbol{q}, \boldsymbol{k}, 0) = R_f (\boldsymbol{q}, 0) R_f (\boldsymbol{k}, 0) = \Vert \boldsymbol{q}\Vert \Vert \boldsymbol{k}\Vert $$The last equality stems from the initial conditions $\boldsymbol{f}(\boldsymbol{q}, 0) = \boldsymbol{q}$ and $\boldsymbol{f}(\boldsymbol{k}, 0) = \boldsymbol{k}$. So now we can simply set $R_f (\boldsymbol{q}, m) = \Vert \boldsymbol{q}\Vert, R_f (\boldsymbol{k}, m) = \Vert \boldsymbol{k}\Vert$, meaning it does not depend on $m$. As for the second equation, substituting $m=n$ similarly gives
$$ \Theta_f (\boldsymbol{q}, m) - \Theta_f (\boldsymbol{k}, m) = \Theta_g (\boldsymbol{q}, \boldsymbol{k}, 0) = \Theta_f (\boldsymbol{q}, 0) - \Theta_f (\boldsymbol{k}, 0) = \Theta (\boldsymbol{q}) - \Theta (\boldsymbol{k}) $$Here, $\Theta (\boldsymbol{q}), \Theta (\boldsymbol{k})$ are the arguments of $\boldsymbol{q}, \boldsymbol{k}$ themselves. The last equality also stems from the initial conditions. According to the above equation, we get $\Theta_f (\boldsymbol{q}, m) - \Theta (\boldsymbol{q}) = \Theta_f (\boldsymbol{k}, m) - \Theta (\boldsymbol{k})$. Therefore, $\Theta_f (\boldsymbol{q}, m) - \Theta (\boldsymbol{q})$ should be a function that depends only on $m$ and is independent of $\boldsymbol{q}$. Let’s denote it as $\varphi(m)$, so $\Theta_f (\boldsymbol{q}, m) = \Theta (\boldsymbol{q}) + \varphi(m)$. Next, substituting $n=m-1$ and rearranging yields
$$ \varphi(m) - \varphi(m-1) = \Theta_g (\boldsymbol{q}, \boldsymbol{k}, 1) + \Theta (\boldsymbol{k}) - \Theta (\boldsymbol{q}) $$This means $\{\varphi(m)\}$ is an arithmetic progression. Let the right side be $\theta$. Then we solve for $\varphi(m) = m\theta$.
Encoding Form#
In summary, we obtain the RoPE in the two-dimensional case represented by complex numbers:
$$ \boldsymbol{f}(\boldsymbol{q}, m) = R_f (\boldsymbol{q}, m)e^{\text{i}\Theta_f(\boldsymbol{q}, m)}= \Vert q\Vert e^{\text{i}(\Theta(\boldsymbol{q}) + m\theta)} = \boldsymbol{q} e^{\text{i}m\theta} $$According to the geometric interpretation of complex multiplication, this transformation actually corresponds to the rotation of a vector. Therefore, we call it “Rotary Position Embedding”. It can also be written in matrix form:
$$ \boldsymbol{f}(\boldsymbol{q}, m) =\begin{pmatrix}\cos m\theta & -\sin m\theta\\ \sin m\theta & \cos m\theta\end{pmatrix} \begin{pmatrix}q_0 \\ q_1\end{pmatrix} $$Since the inner product satisfies linearity, any even-dimensional RoPE can be represented as a concatenation of two-dimensional cases, i.e.,
$$ \scriptsize{\underbrace{\begin{pmatrix}\cos m\theta_0 & -\sin m\theta_0 & 0 & 0 & \cdots & 0 & 0 \\\sin m\theta_0 & \cos m\theta_0 & 0 & 0 & \cdots & 0 & 0 \\0 & 0 & \cos m\theta_1 & -\sin m\theta_1 & \cdots & 0 & 0 \\0 & 0 & \sin m\theta_1 & \cos m\theta_1 & \cdots & 0 & 0 \\\vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\0 & 0 & 0 & 0 & \cdots & \cos m\theta_{d/2-1} & -\sin m\theta_{d/2-1} \\0 & 0 & 0 & 0 & \cdots & \sin m\theta_{d/2-1} & \cos m\theta_{d/2-1}\end{pmatrix}}_{\boldsymbol{\mathcal{R}}_m} \begin{pmatrix}q_0 \\ q_1 \\ q_2 \\ q_3 \\ \vdots \\ q_{d-2} \\ q_{d-1}\end{pmatrix}} $$That is to say, multiply the vector $\boldsymbol{q}$ at position $m$ by the matrix $\boldsymbol{\mathcal{R}}_m$, and the vector $\boldsymbol{k}$ at position $n$ by the matrix $\boldsymbol{\mathcal{R}}_n$. Using the transformed $\boldsymbol{Q}, \boldsymbol{K}$ sequences for Attention, the Attention automatically incorporates relative position information because the following identity holds:
$$ (\boldsymbol{\mathcal{R}}_m \boldsymbol{q})^{\top}(\boldsymbol{\mathcal{R}}_n \boldsymbol{k}) = \boldsymbol{q}^{\top} \boldsymbol{\mathcal{R}}_m^{\top}\boldsymbol{\mathcal{R}}_n \boldsymbol{k} = \boldsymbol{q}^{\top} \boldsymbol{\mathcal{R}}_{n-m} \boldsymbol{k} $$It is worth noting that $\boldsymbol{\mathcal{R}}_m$ is an orthogonal matrix, which does not change the length of the vector. Therefore, generally speaking, it will not affect the stability of the original model.
Due to the sparsity of $\boldsymbol{\mathcal{R}}_m$, implementing it directly with matrix multiplication would be very inefficient in terms of computational power. It is recommended to implement RoPE in the following way:
$$ \begin{pmatrix}q_0 \\ q_1 \\ q_2 \\ q_3 \\ \vdots \\ q_{d-2} \\ q_{d-1}\end{pmatrix}\otimes\begin{pmatrix}\cos m\theta_0 \\ \cos m\theta_0 \\ \cos m\theta_1 \\ \cos m\theta_1 \\ \vdots \\ \cos m\theta_{d/2-1} \\ \cos m\theta_{d/2-1}\end{pmatrix} + \begin{pmatrix}-q_1 \\ q_0 \\ -q_3 \\ q_2 \\ \vdots \\ -q_{d-1} \\ q_{d-2}\end{pmatrix}\otimes\begin{pmatrix}\sin m\theta_0 \\ \sin m\theta_0 \\ \sin m\theta_1 \\ \sin m\theta_1 \\ \vdots \\ \sin m\theta_{d/2-1} \\ \sin m\theta_{d/2-1}\end{pmatrix} $$Here, $\otimes$ denotes element-wise multiplication, which is the $*$ operation in computational frameworks like Numpy and Tensorflow. From this implementation, it can also be seen that RoPE can be regarded as a variant of multiplicative position embedding.
Long-Range Attenuation#
As can be seen, RoPE is somewhat similar in form to Sinusoidal Position Embedding, except that Sinusoidal Position Embedding is additive, while RoPE can be regarded as multiplicative. Regarding the choice of $\theta_i$, we also followed the scheme of Sinusoidal Position Embedding, namely $\theta_i = 10000^{-2i/d}$, which can bring a certain degree of long-range attenuation.
The detailed proof is as follows: After grouping $\boldsymbol{q}, \boldsymbol{k}$ pairwise, their inner product after adding RoPE can be expressed using complex multiplication as
$$ (\boldsymbol{\mathcal{R}}_m \boldsymbol{q})^{\top}(\boldsymbol{\mathcal{R}}_n \boldsymbol{k}) = \text{Re}\left[\sum_{i=0}^{d/2-1}\boldsymbol{q}_{[2i:2i+1]}\boldsymbol{k}_{[2i:2i+1]}^* e^{\text{i}(m-n)\theta_i}\right] $$Let $h_i = \boldsymbol{q}_{[2i:2i+1]}\boldsymbol{k}_{[2i:2i+1]}^*$ and $S_j = \sum\limits_{i=0}^{j-1} e^{\text{i}(m-n)\theta_i}$. Let’s define $h_{d/2}=0$ and $S_0=0$. Then, by Abel’s transform (Summation by parts), we get:
$$ \sum_{i=0}^{d/2-1}\boldsymbol{q}_{[2i:2i+1]}\boldsymbol{k}_{[2i:2i+1]}^* e^{\text{i}(m-n)\theta_i} = \sum_{i=0}^{d/2-1} h_i (S_{i+1} - S_i) = -\sum_{i=0}^{d/2-1} S_{i+1}(h_{i+1} - h_i) $$Therefore
$$ \begin{aligned}\left|\sum_{i=0}^{d/2-1}\boldsymbol{q}_{[2i:2i+1]}\boldsymbol{k}_{[2i:2i+1]}^* e^{\text{i}(m-n)\theta_i}\right| =&\, \left|\sum_{i=0}^{d/2-1} S_{i+1}(h_{i+1} - h_i)\right| \\\leq&\, \sum_{i=0}^{d/2-1} |S_{i+1}| |h_{i+1} - h_i| \\\leq&\, \left(\max_i |h_{i+1} - h_i|\right)\sum_{i=0}^{d/2-1} |S_{i+1}|\end{aligned} $$Thus, we can examine how $\frac{1}{d/2}\sum\limits_{i=1}^{d/2} |S_i|$ changes with relative distance as an indicator of attenuation. The Mathematica code is as follows:
| |
The result is shown in the figure below:
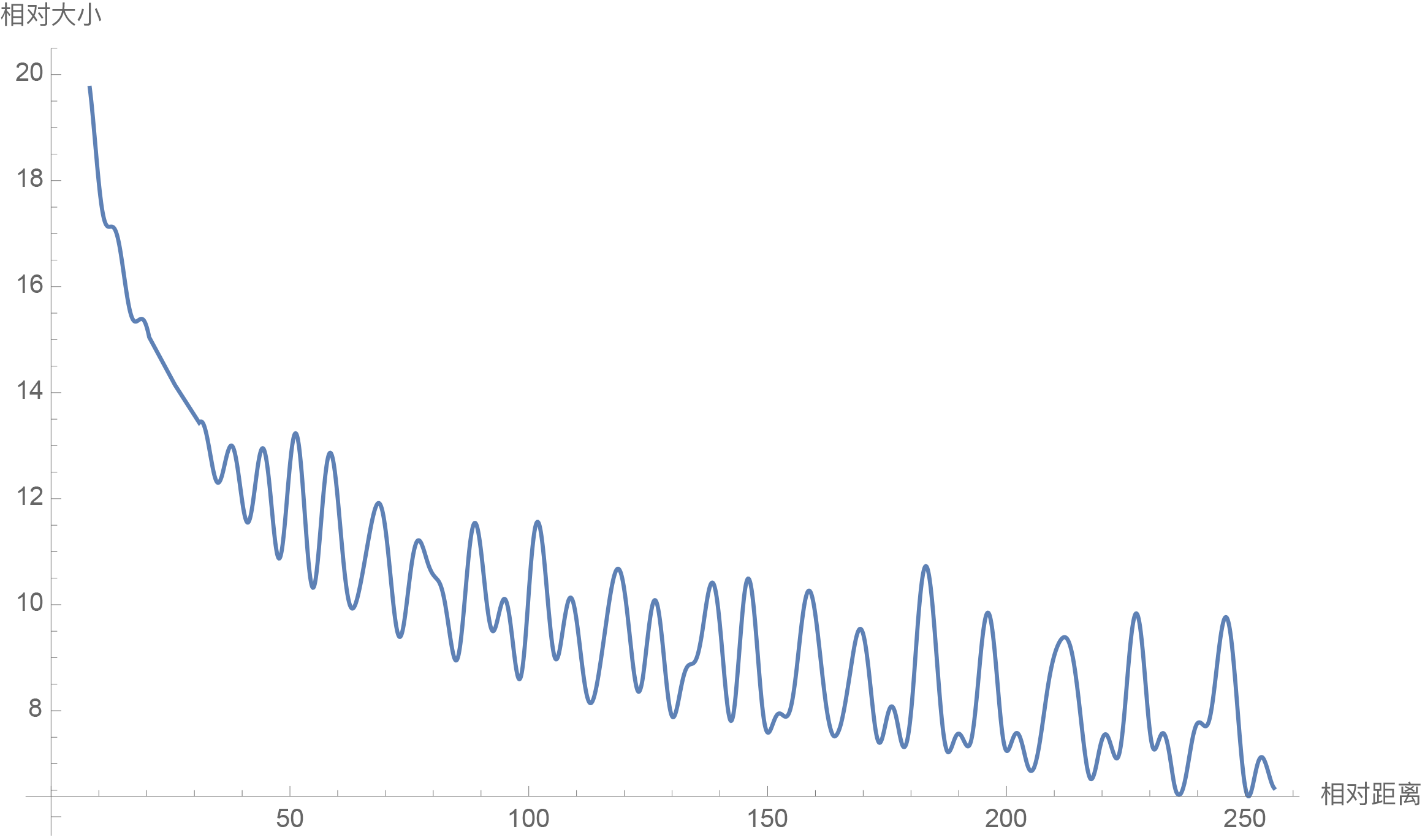
From the figure, we can see that as the relative distance increases, the inner product result shows a trend of attenuation. Therefore, choosing $\theta_i = 10000^{-2i/d}$ indeed brings a certain degree of long-range attenuation. Of course, as mentioned in the previous article, this is not the only choice that can bring long-range attenuation; almost any smooth monotonic function can. Here, we simply adopted the existing choice. The author also tried initializing with $\theta_i = 10000^{-2i/d}$ and treating $\theta_i$ as a trainable parameter. After training for a period, it was found that $\theta_i$ did not update significantly, so it was decided to simply fix $\theta_i = 10000^{-2i/d}$.
Linear Scenario#
Finally, we point out that RoPE is currently the only relative position encoding that can be used with linear Attention. This is because other relative position encodings operate directly on the Attention matrix. However, linear Attention does not compute the Attention matrix beforehand, so there is no way to operate on the Attention matrix, and thus other methods cannot be applied to linear Attention. For RoPE, it implements relative position encoding using the method of absolute position encoding and does not require operating on the Attention matrix, thus making it possible to apply it to linear Attention.
We will not repeat the introduction to linear Attention here. Readers who are interested can refer to 《Exploring Linear Attention: Does Attention Have to Have a Softmax?》. A common form of linear Attention is:
$$ Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V})_i = \frac{\sum\limits_{j=1}^n \text{sim}(\boldsymbol{q}_i, \boldsymbol{k}_j)\boldsymbol{v}_j}{\sum\limits_{j=1}^n \text{sim}(\boldsymbol{q}_i, \boldsymbol{k}_j)} = \frac{\sum\limits_{j=1}^n \phi(\boldsymbol{q}_i)^{\top} \varphi(\boldsymbol{k}_j)\boldsymbol{v}_j}{\sum\limits_{j=1}^n \phi(\boldsymbol{q}_i)^{\top} \varphi(\boldsymbol{k}_j)} $$Where $\phi, \varphi$ are activation functions with non-negative range. As can be seen, linear Attention is also based on the inner product, so a natural idea is to insert RoPE into the inner product:
$$ \frac{\sum\limits_{j=1}^n [\boldsymbol{\mathcal{R}}_i\phi(\boldsymbol{q}_i)]^{\top} [\boldsymbol{\mathcal{R}}_j\varphi(\boldsymbol{k}_j)]\boldsymbol{v}_j}{\sum\limits_{j=1}^n [\boldsymbol{\mathcal{R}}_i\phi(\boldsymbol{q}_i)]^{\top} [\boldsymbol{\mathcal{R}}_j\varphi(\boldsymbol{k}_j)]} $$However, the problem with this is that the inner product $[\boldsymbol{\mathcal{R}}_i\phi(\boldsymbol{q}_i)]^{\top} [\boldsymbol{\mathcal{R}}_j\varphi(\boldsymbol{k}_j)]$ may be negative, so it is no longer conventional probabilistic attention. Moreover, the denominator risks becoming zero, which may lead to optimization instability. Considering that $\boldsymbol{\mathcal{R}}_i, \boldsymbol{\mathcal{R}}_j$ are orthogonal matrices and do not change the vector length, we can discard the conventional requirement for probabilistic normalization and use the following operation as a new form of linear Attention:
$$ \frac{\sum\limits_{j=1}^n [\boldsymbol{\mathcal{R}}_i\phi(\boldsymbol{q}_i)]^{\top} [\boldsymbol{\mathcal{R}}_j\varphi(\boldsymbol{k}_j)]\boldsymbol{v}_j}{\sum\limits_{j=1}^n \phi(\boldsymbol{q}_i)^{\top} \varphi(\boldsymbol{k}_j)} $$That is to say, RoPE is inserted only into the numerator, while the denominator remains unchanged. This form of attention is no longer probability-based (the attention matrix no longer satisfies non-negativity and normalization), but in some sense, it is still a normalization scheme. Furthermore, there is no evidence to suggest that non-probabilistic attention is necessarily bad (for instance, Nyströmformer also constructs attention not strictly based on probability distribution). Thus, we are experimenting with it as one of the candidate schemes, and our preliminary experimental results show that this kind of linear Attention is also effective.
Additionally, the author proposed another linear Attention scheme in 《Exploring Linear Attention: Does Attention Have to Have a Softmax?》: $\text{sim}(\boldsymbol{q}_i, \boldsymbol{k}_j) = 1 + \left( \frac{\boldsymbol{q}_i}{\Vert \boldsymbol{q}_i\Vert}\right)^{\top}\left(\frac{\boldsymbol{k}_j}{\Vert \boldsymbol{k}_j\Vert}\right)$. This scheme does not rely on the non-negativity of the value range, and RoPE also does not change the vector length. Therefore, RoPE can be directly applied to this type of linear Attention without changing its probabilistic meaning.
Model Open Source#
The first version of the RoFormer model has been trained and open-sourced on Github:
Simply speaking, RoFormer is a WoBERT model where the absolute position encoding is replaced with RoPE. Its structure comparison with other models is as follows:
| BERT | WoBERT | NEZHA | RoFormer | |
|---|---|---|---|---|
| Token Unit | Character | Word | Character | Word |
| Position Encoding | Absolute Position | Absolute Position | Classic Relative Position | RoPE |
For pre-training, we used WoBERT Plus as the base and adopted alternating training with multiple sequence lengths and batch sizes to allow the model to adapt to different training scenarios in advance:
| maxlen | batch size | Training Steps | Final Loss | Final Acc | |
|---|---|---|---|---|---|
| 1 | 512 | 256 | 200k | 1.73 | 65.0% |
| 2 | 1536 | 256 | 12.5k | 1.61 | 66.8% |
| 3 | 256 | 256 | 120k | 1.75 | 64.6% |
| 4 | 128 | 512 | 80k | 1.83 | 63.4% |
| 5 | 1536 | 256 | 10k | 1.58 | 67.4% |
| 6 | 512 | 512 | 30k | 1.66 | 66.2% |
As can also be seen from the table, increasing the sequence length actually improves the pre-training accuracy. This reflects the effectiveness of RoFormer in handling long-text semantics and also demonstrates the good extrapolation capability of RoPE. On short-text tasks, RoFormer performs similarly to WoBERT. The main feature of RoFormer is its ability to directly process text of arbitrary length. Below are our experimental results on the CAIL2019-SCM task:
| Validation Set | Test Set | |
|---|---|---|
| BERT-512 | 64.13% | 67.77% |
| WoBERT-512 | 64.07% | 68.10% |
| RoFormer-512 | 64.13% | 68.29% |
| RoFormer-1024 | 66.07% | 69.79% |
Here, the parameter after $\text{-}$ is the maximum length truncated during fine-tuning. It can be seen that RoFormer can indeed handle long-text semantics well. As for hardware requirements, running with maxlen=1024 on a card with 24G VRAM, the batch_size can be 8 or more. Currently, this is the only task the author has found in Chinese suitable for testing long-text capability, so only this task was tested for long texts. Readers are welcome to test or recommend other evaluation tasks.
Of course, although theoretically RoFormer can handle sequences of arbitrary length, the current RoFormer still has quadratic complexity. We are also training a RoFormer model based on linear Attention, which will be open-sourced after the experiments are completed. Please look forward to it.
** (Note: RoPE and RoFormer have been compiled into a paper 《RoFormer: Enhanced Transformer with Rotary Position Embedding》 and submitted to Arxiv. Feel free to use and cite haha~) **
Summary (formatted)#
This article introduced our self-developed Rotary Position Embedding (RoPE) and the corresponding pre-trained model, RoFormer. Theoretically, RoPE shares some similarities with Sinusoidal Position Embedding, but RoPE does not rely on Taylor expansion and is more rigorous and interpretable. From the results of the pre-trained model RoFormer, RoPE exhibits good extrapolation capability and shows good long-text processing ability when applied in Transformer. Furthermore, RoPE is currently the only relative position encoding that can be used with linear Attention.
| |