7. Length Extrapolation and Local Attention

For Transformer models, length extrapolation is a desirable property we’ve always pursued. It refers to the ability of a model trained on short sequences to be used on long sequences without fine-tuning, while still maintaining good performance. We pursue length extrapolation partly for theoretical completeness, feeling it’s a property an ideal model should possess, and partly for training practicality, allowing us to train a model usable for long sequences at a lower cost (on shorter sequences).

Below, we will analyze the key ideas for strengthening the length extrapolation of Transformers and propose a “super strong baseline” approach. Then, we will use this “super strong baseline” to analyze some related research work.

Misconceptions

#

The first work to explicitly study Transformer length extrapolation should be ALIBI, which came out in mid-2021, not too long ago. Why did it take so long (compared to Transformer’s first publication in 2017) for someone to specifically address this topic? It’s likely because for a long time, we took it for granted that Transformer’s length extrapolation was a positional encoding problem, and finding a better positional encoding would suffice.

Indeed, by comparing the extrapolation effects of existing positional encodings, some arguments supporting this view can be found. For example, several experimental results shared later show that the length extrapolation of relative positional encoding is, on average, better than that of absolute positional encoding. Functional relative positional encodings like RoPE have better extrapolation effects than learned relative positional encodings. So, it seems that as long as we keep optimizing the form of positional encoding, we will eventually provide Transformers with better length extrapolation, thus solving this problem. However, the situation is not that optimistic. Even positional encodings with good extrapolation capabilities like RoPE can only extrapolate lengths by about 10% to 20% while maintaining performance; beyond that, the performance drops sharply. This ratio is too far from expectations; ideally, extrapolating several times the length would be considered valuable extrapolation. Therefore, it’s not hard to imagine that relying solely on improving positional encoding to enhance Transformer’s length extrapolation will take who knows how long to achieve better effects for longer sequences.

Intuitively, many readers believe that functional positional encodings like Sinusoidal or RoPE, having no training parameters, should have very good length extrapolation. However, this is not the case; these types of positional encodings have not shown any significant advantage in length extrapolation. Why is this? In fact, when assuming the extrapolation of functional positional encodings, people forget their basic premise—“smoothness.”

Extrapolation is essentially inferring the whole from the local. We should be familiar with this concept; Taylor series approximation is a classic example. It only requires knowing the values of a function’s derivatives at a certain point to effectively estimate values within a neighborhood, relying on the high-order smoothness of the given function (existence and boundedness of high-order derivatives). But are Sinusoidal or RoPE such functions? No. They are combinations of a series of sine and cosine functions, with phase functions like $k/10000^{2i/d}$. When $2i/d\approx 0$, the function is approximately $\sin k, \cos k$, which are high-frequency oscillating functions with respect to the position $k$, not straight lines or functions that asymptotically approach a straight line. Therefore, models based on them often exhibit unpredictable extrapolation behavior. Is it possible to design non-oscillating positional encodings? It’s difficult. If a positional encoding function doesn’t oscillate, it often lacks sufficient capacity to encode enough positional information. In a sense, the complexity of the positional encoding function itself is a requirement for encoding positions.

Super Strong Baseline

#

In fact, a more accurate definition should be:

Length extrapolation is a problem of inconsistency between training and prediction lengths.

Specifically, there are two points of inconsistency:

1. Untrained positional encodings (whether absolute or relative) are used during prediction.

2. The number of tokens processed by the attention mechanism during prediction significantly exceeds the number during training.

Point 1 is likely easy for everyone to understand: if it hasn’t been trained, there’s no guarantee it can be handled well. This is a very realistic phenomenon in DL, even for functional positional encodings like Sinusoidal or RoPE. Regarding point 2, readers might be a bit confused. Doesn’t Attention theoretically handle sequences of arbitrary length? How does inconsistency in training and prediction lengths affect anything? The answer is entropy. We analyzed this issue in 《Understanding Attention’s Scale Operation from Entropy Invariance》. The more tokens are averaged in attention, the more “uniform” the final distribution tends to be (higher entropy), meaning attention is more dispersed. Conversely, shorter training length means lower attention entropy and more concentrated attention. This is also a difference between training and prediction, and it affects performance.

In fact, for Transformer models with relative positional encoding, using a very simple Attention Mask can solve both of these problems simultaneously and achieve performance close to SOTA:

It’s easy to see that this transforms the Attention during prediction into a local Attention, where each token can only see tokens within the training length. This way, the number of tokens each token can see is consistent with training, solving problem 2. Simultaneously, because it’s relative positional encoding, positional counting is centered at the current token. Therefore, such local Attention won’t use more unknown encodings than during training, solving problem 1. Thus, this simple Attention Mask simultaneously solves the two difficulties of length extrapolation and doesn’t require retraining the model. What’s even more astonishing is that various experimental results show that if this is used as a baseline, the relative improvement of various similar works becomes minimal, meaning it itself is already very close to SOTA. It can be called a fast and good “super strong baseline.”

Paper Study

#

Since ALIBI, quite a few works have been dedicated to the study of Transformer length extrapolation. In this section, the author has studied and organized some representative works. From these, we can also find that they fundamentally share many similarities with the baseline model, and can even be said to be variations of the baseline model in some sense. This further highlights the deep connection between length extrapolation and the locality of attention.

ALIBI

#

As the “pioneering work,” ALIBI is unavoidable. It comes from the paper 《Train Short, Test Long: Attention with Linear Biases Enables Input Length Extrapolation》. In retrospect, the change made by ALIBI is very simple: before Softmax, the Attention calculation is changed from $\boldsymbol{q}_m^{\top}\boldsymbol{k}_n$ to

where $\lambda > 0$ is a hyperparameter, with different values set for each head. From this definition, one can see the similarity between ALIBI and the baseline model: both subtract a non-negative matrix before Softmax, differing only in the specific non-negative matrix subtracted. ALIBI can be seen as a “smooth version” of the baseline model:

ALIBI is a very simple (and certainly effective) smooth local attention technique. However, interpreting it as “positional encoding” might not be entirely appropriate. If we apply it to bidirectional attention according to equation $\text{eq:alibi}$, then since $|m - n|=|n - m|$, theoretically the model cannot distinguish between “left” and “right,” only recognizing the magnitude of relative distance, which obviously cannot accurately recognize positional information. The reason it works well in unidirectional language models is that unidirectional language models can achieve non-trivial performance (significantly higher than random) even without any positional encoding. The local attention applied by ALIBI enhances locality, fitting the inherent characteristics of the language model task itself.

KERPLE

#

KERPLE is from the paper 《KERPLE: Kernelized Relative Positional Embedding for Length Extrapolation》. It is essentially a simple generalization of ALIBI, introducing two training parameters $r_1,r_2$ to generalize equation $\text{eq:alibi}$:

Another generalization with trainable parameters. It’s not surprising that KERPLE achieves better results than ALIBI. However, here I must severely criticize the obfuscation in the KERPLE paper. According to the layout, the third section of the original paper is the theoretical basis, but it’s clearly irrelevant content introduced merely to forcibly increase the mathematical depth of the article, offering no help in understanding KERPLE and even reducing the reader’s interest (to put it bluntly, it serves the reviewers, not the readers).

Sandwich

#

Sandwich is also from the authors of KERPLE, from 《Receptive Field Alignment Enables Transformer Length Extrapolation》, uploaded to Arxiv just last month. It replaces equation $\text{eq:alibi}$ with

where $\boldsymbol{p}_m,\boldsymbol{p}_n$ are Sinusoidal positional encodings, and $\lambda > 0$ is a hyperparameter. From 《Transformer Upgrades: 1. Tracing the Origins of Sinusoidal Positional Encoding》, we know that $\boldsymbol{p}_m^{\top}\boldsymbol{p}_n$ is a scalar function of $m-n$, and on average it is a monotonically increasing function of $|m-n|$. Thus, its effect is also similar to $-\lambda|m-n|$. The reason for emphasizing “on average” is that $\boldsymbol{p}_m^{\top}\boldsymbol{p}_n$ as a whole is not strictly monotonic, but oscillates downwards, as shown in the figure:

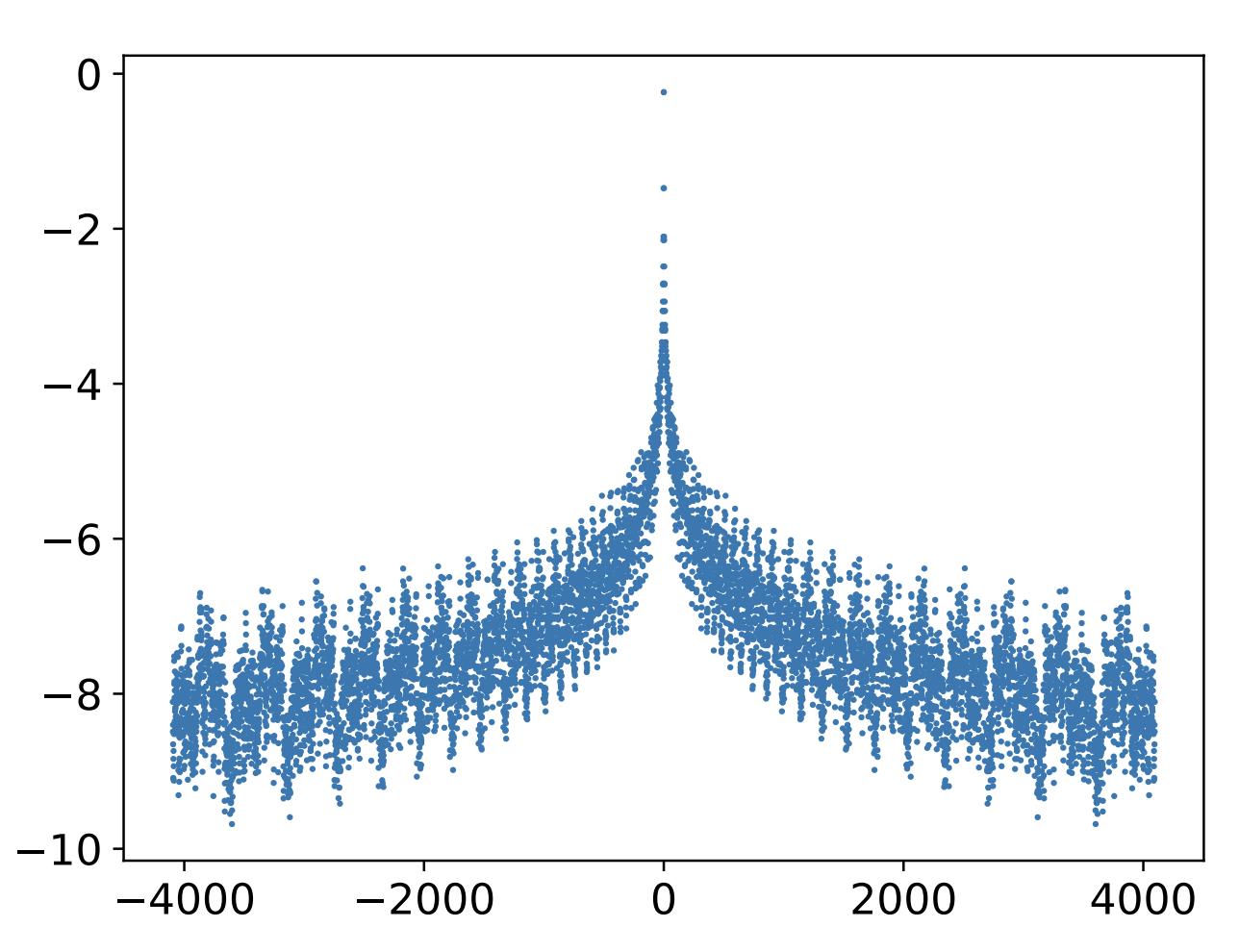
If necessary, we can also convert Sandwich into the form of “RoPE-like absolute positional encoding achieving relative positional encoding.” This only requires noticing that

meaning Sandwich supplements absolute positional information through concatenation, and its Attention result is equivalent to relative positional encoding. However, currently, this conversion has only theoretical value because concatenation increases the vector dimension, further increasing the computational cost of Attention.

XPOS

#

XPOS comes from the paper 《A Length-Extrapolatable Transformer》, appearing on Arxiv the same day as Sandwich. It is a continuation and generalization of RoPE. We know that the basic solution for RoPE is:

where $\boldsymbol{\mathcal{R}}_n=\begin{pmatrix}\cos n\theta & - \sin n\theta\\ \sin n\theta & \cos n\theta\end{pmatrix}$. When the author derived RoPE, it was assumed that “$Q$ and $K$ undergo the same transformation.” In fact, purely from the perspective of “absolute position implementing relative position,” there is no necessity to restrict the transformation format of the two to be consistent. For example, XPOS considers

where $\xi$ is a scalar hyperparameter. Thus,

The overall result still depends only on the relative position $m-n$. However, the problem now is that the exponent is $m-n$ instead of $|m-n|$. As long as $\xi\neq 1$, one side will diverge. The cleverness of XPOS is that it chose a scenario focused on (like many related works)—unidirectional language models—thus only using attention for the $m\geq n$ part! In this case, choosing $\xi\in(0,1)$ achieves an effect that decays with relative distance.

In fact, the additional exponential decay term $\xi^m$ was not first introduced by XPOS. Among the literature the author has read, the same term first appeared in PermuteFormer, although PermuteFormer primarily focuses on linear Attention scenarios. In terms of details, XPOS assigns different $\xi$ values to each block, but in private communication with the author, they performed additional experiments sharing the same $\xi$ and found that the improvement from setting different $\xi$ values was almost negligible. Additionally, we need to appropriately control the value of $\xi$ to prevent $\xi^{-n}$ from overflowing when $n$ is large.

It is worth noting that the decay with relative distance here is multiplied directly before the Softmax Attention Score. The result is that scores for relatively distant positions become very close to 0, rather than approaching negative infinity as in the previous designs. $e^0$ does not have the effect of approaching zero, so this design is not a variant of local Attention. Therefore, its effect did not reach SOTA. To compensate for this gap, XPOS designed a special local Attention (called Blockwise Causal Attention, abbreviated BCA), which, when added, closes the gap. During communication, the authors stated that they used BCA because of implementation advantages, but in practice, the baseline model’s local Attention is more effective. So, for extrapolation, local attention is still key.

The experiments in the original paper are very rich and worth referencing. I recommend everyone read it carefully~

Summary (formatted)

#

This article summarizes related work aimed at enhancing the length extrapolation capability of the Transformer. It includes a simple but powerful baseline approach and several related works focusing on length extrapolation. From these, we can find that these works are essentially variants of the baseline approach—local attention. Local attention is one of the key components for length extrapolation.

@online{kexuefm-9431,
        title={Transformer Upgrades: 7. Length Extrapolation and Local Attention},
        author={苏剑林},
        year={2023},
        month={01},
        url={\url{https://kexue.fm/archives/9431}},
}