10. RoPE is a β-Based Encoding

For readers interested in how to extend the context length of LLMs, last week was undoubtedly exciting, with a continuous stream of inspiring results emerging from the open-source community. First, netizen @kaiokendev experimented with a “positional linear interpolation” scheme in his project SuperHOT, showing that existing LLMs can handle Long Context with very little long text fine-tuning. Almost simultaneously, Meta proposed the same idea, publishing a paper 《Extending Context Window of Large Language Models via Positional Interpolation》 with rich experimental results. The surprises didn’t stop there; subsequently, netizen @bloc97 proposed NTK-aware Scaled RoPE, achieving the effect of extending the Context length without fine-tuning!

All these developments, especially NTK-aware Scaled RoPE, compelled the author to re-examine the meaning of RoPE. After analysis, the author found that the construction of RoPE can be viewed as a $\beta$-based encoding. From this perspective, the progress in the open-source community can be understood as different ways of augmenting this base encoding.

Base Representation

#

Suppose we have an integer $n$ less than 1000 (excluding 1000) that needs to be input into a model as conditional input. What would be a good way to do this?

The most naive idea is to input it directly as a one-dimensional floating-point vector. However, the range from 0 to 999 covers a span of nearly a thousand, which is not easy for gradient-based optimizers to handle effectively. How about scaling it to be between 0 and 1? That’s not much better, because the adjacent difference changes from 1 to 0.001, making it difficult for the model and optimizer to distinguish neighboring numbers. In general, gradient-based optimizers are a bit “picky”; they can only handle inputs that are neither too large nor too small; problems easily arise with values outside this range.

Therefore, to avoid this issue, we need to devise new input methods. When we don’t know how to let a machine process something, we might consider how humans handle it. For an integer, such as 759, this is a three-digit number in base 10, with each digit being from 0 to 9. Since we ourselves use base 10 to represent numbers, why not directly input the base 10 representation into the model? That is, we input the integer $n$ as a three-dimensional vector $[a, b, c]$, where $a, b, c$ are the hundreds, tens, and units digits of $n$, respectively. This way, we not only reduce the range of the numbers but also maintain the difference between adjacent numbers, at the cost of increasing the input dimension—which is fine, as neural networks are good at processing high-dimensional data.

If we want to further reduce the range of the numbers, we can further shrink the base of the numeral system, such as using base 8, base 6, or even base 2, at the cost of further increasing the input dimension.

Direct Extrapolation

#

Suppose we trained a model using a three-dimensional base 10 representation, and the model performs well. Then suddenly, a new requirement comes up: increase the upper limit of $n$ to within 2000. How should we handle this?

If we still input it as a base 10 vector into the model, the input would now be a four-dimensional vector. However, the original model was designed and trained for three-dimensional vectors, so it cannot handle the input with an added dimension. Some readers might wonder why we don’t reserve enough dimensions in advance. Yes, it’s possible to reserve a few extra dimensions beforehand, setting them to 0 during training and changing them to other numbers during inference. This is extrapolation.

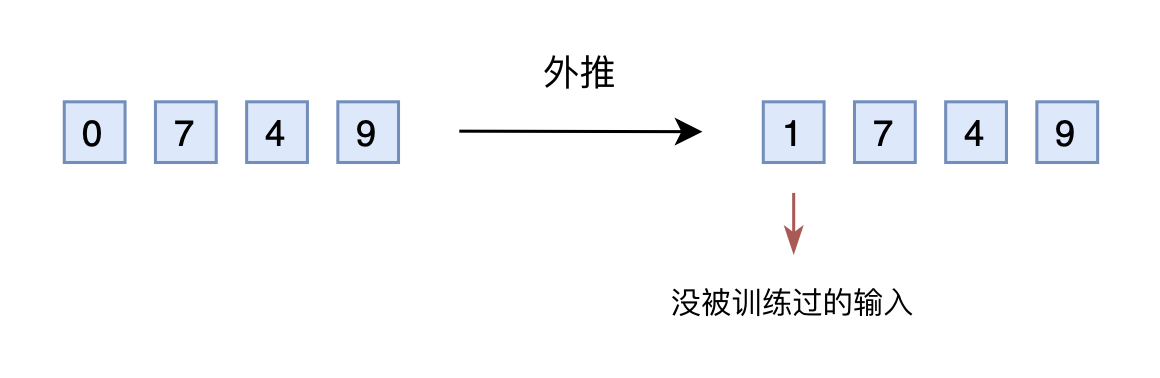
However, the reserved dimensions were always 0 during the training phase. If they are changed to other numbers during the inference phase, the performance may not be good, as the model might not be adaptive to situations it hasn’t been trained on. In other words, due to insufficient training data for certain dimensions, direct extrapolation usually leads to a severe degradation in model performance.

Linear Interpolation

#

So, someone came up with the idea of changing extrapolation to interpolation. Simply put, this means compressing numbers within 2000 to within 1000, for example, by dividing by 2. So 1749 becomes 874.5, which is then converted into a three-dimensional vector [8, 7, 4.5] and input into the original model. From an absolute value perspective, the new $[7, 4, 9]$ actually corresponds to 1498, which is twice the original correspondence; the mapping method is inconsistent. From a relative value perspective, the original difference between adjacent numbers was 1, now it is 0.5, and the last dimension is more “crowded.” Therefore, after making the interpolation modification, fine-tuning is usually required for the model to re-adapt to the crowded mapping relationship.

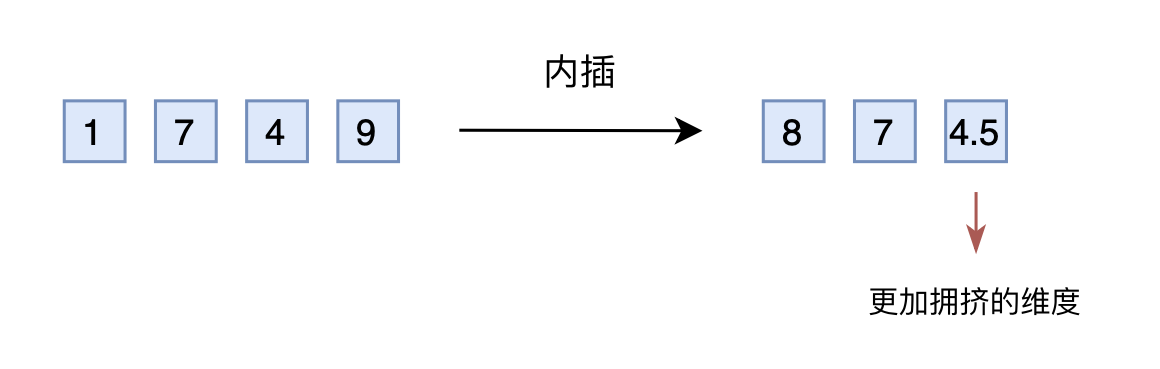
Of course, some readers will say that the extrapolation scheme can also be fine-tuned. Yes, but the interpolation scheme requires far fewer steps for fine-tuning because in many scenarios (such as positional encoding), the relative size (or perhaps the order information) is more important. In other words, the model only needs to know that 874.5 is greater than 874, not what actual large number it represents. And the original model has already learned that 875 is greater than 874, and coupled with the model’s inherent generalization ability, learning that 874.5 is greater than 874 is not too difficult.

However, the interpolation scheme is not perfect either. When the processing range further increases, the adjacent difference becomes even smaller, and this reduction in adjacent difference is concentrated in the units digit, while the hundreds and tens digits still retain an adjacent difference of 1. In other words, the interpolation method causes the distribution of different dimensions to become uneven, making each dimension unequal, and further increasing the difficulty for the model to learn.

Base Conversion

#

Is there a solution that does not require adding dimensions and can also maintain the adjacent difference? Yes, we might be very familiar with it: base conversion! A three-digit base 10 encoding can represent 0 to 999. What about base 16? It can represent up to $16^3 - 1 = 4095 > 1999$. Therefore, by simply converting to base 16, such as 1749 becoming $[6, 13, 5]$, a three-dimensional vector can cover the target range. The cost is that the digits in each dimension change from 0–9 to 0–15.

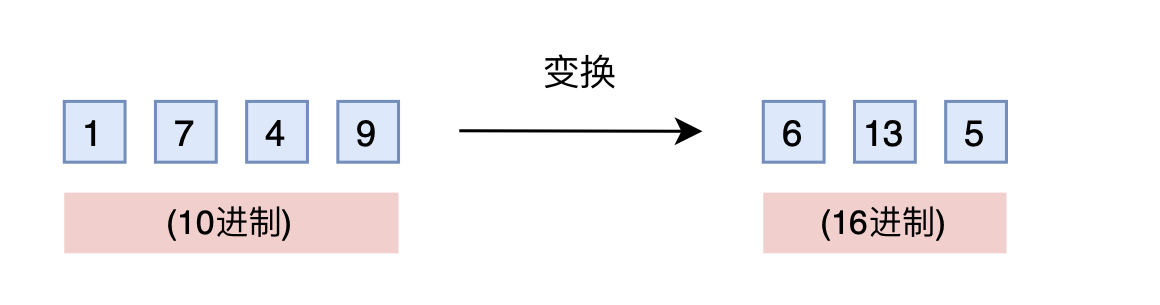
If you think about it carefully, you’ll find this is a brilliant idea. As mentioned earlier, the scenarios we care about primarily use order information. The original trained model has already learned that $875 > 874$. In base 16, $875 > 874$ also holds, and the comparison rules are exactly the same (the model doesn’t know what base you’re inputting). The only concern is whether the model can still compare normally when each dimension exceeds 9 (10–15). But in fact, a general model also has some generalization ability, so extrapolating each dimension slightly is fine. Therefore, this idea of converting the base might even be effective without fine-tuning the original model! Furthermore, to further narrow the extrapolation range, we can use base $\left\lceil\sqrt[3]{2000}\right\rceil =13$ instead of base 16.

As we will see next, this base conversion idea actually corresponds to the NTK-aware Scaled RoPE mentioned at the beginning of the article!

Positional Encoding

#

To establish the connection between them, we first need to establish the following result:

The rotary positional encoding (RoPE) for position $n$ is essentially the $\beta$-based encoding of the number $n$!

This might seem surprising, as the two appear completely different on the surface. But in fact, their operations share identical key properties. To understand this, let’s first recall a number $n$ in base 10. If we want to find its $\beta$-based representation, specifically the digit at the $m$-th position (counting from right to left), the method is:

That is, first divide by $\beta^{m-1}$ power, then take the modulus (remainder). Now let’s recall RoPE. Its construction is based on Sinusoidal positional encoding, which can be rewritten as:

where $\beta=10000^{2/d}$. Now, compare with equation $\text{eq:mod}$. Does equation $\text{eq:sinu}$ not also have the identical $\frac{n}{\beta^{m-1}}$? As for the modulo operation, its most important property is periodicity. Are the $\cos, \sin$ in equation $\text{eq:sinu}$ not just periodic functions? Therefore, aside from the trivial difference of the floor function, RoPE (or rather, Sinusoidal positional encoding) is actually the $\beta$-based encoding of the number $n$!

With this connection established, the integer $n$ augmentation schemes discussed in the previous sections can correspond to the various developments mentioned at the beginning of the article. Among them, the direct extrapolation scheme is to change nothing, the interpolation scheme is to replace $n$ with $n/k$, where $k$ is the factor of expansion. This is exactly the Positional Interpolation scheme experimented with in Meta’s paper, and their experimental results also prove that extrapolation does require more fine-tuning steps than interpolation.

As for base conversion, it’s about expanding the representation range by a factor of $k$. Then the original $\beta$-based system must be expanded to at least a $\beta (k^{2/d})$-based system (although equation $\text{eq:sinu}$ is a $d$-dimensional vector, $\cos$ and $\sin$ appear in pairs, so it’s equivalent to a $d/2$-digit $\beta$-based representation, thus needing the $d/2$-th root instead of the $d$-th root), or equivalently, replacing the original base $10000$ with $10000k$. This is basically NTK-aware Scaled RoPE. As discussed earlier, since positional encoding relies more on order information, and base conversion fundamentally doesn’t change the order comparison rules, NTK-aware Scaled RoPE also achieves good results on longer Contexts without fine-tuning.

Tracing the Origins

#

Some readers might be curious about the connection to NTK. NTK stands for “Neural Tangent Kernel,” which we briefly touched upon in 《Viewing Optimization Algorithms from a Dynamics Perspective (VII): SGD ≈ SVM?》. The relationship between the above results and NTK is more due to the academic background of the proposer. The proposer is familiar with results like 《Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains》, which uses NTK-related results to prove that neural networks cannot directly learn high-frequency signals. The solution is to transform them into Fourier features—whose form is similar to the Sinusoidal positional encoding in equation $\text{eq:mod}$.

Therefore, based on the intuition from NTK-related results, the proposer derived NTK-aware Scaled RoPE. I consulted the proposer about his derivation. In fact, his derivation is very simple: it combines extrapolation and interpolation—extrapolate high frequencies, interpolate low frequencies. Specifically, the lowest frequency term in equation $\text{eq:sinu}$ is $\frac{n}{\beta^{d/2-1}}$. Introducing a parameter $\lambda$, it becomes $\frac{n}{(\beta\lambda)^{d/2-1}}$. To make it consistent with interpolation, i.e.,

Solving for $\lambda$ gives $\lambda=k^{2/(d-2)}$. As for the highest frequency term, $\frac{n}{\beta}$, introducing $\lambda$ makes it $\frac{n}{\beta\lambda}$. Since $d$ is usually large, $\lambda$ is very close to 1, so it is still close to $\frac{n}{\beta}$, which is equivalent to extrapolation.

So this scheme cleverly combines extrapolation and interpolation. Additionally, since $d$ is relatively large (BERT is 64, LLAMA is 128), $k^{2/(d-2)}$ is not much different from $k^{2/d}$, so it is basically consistent with the $k^{2/d}$ solution I proposed based on the base idea. Also, from the proposer’s idea, any scheme that can achieve “high-frequency extrapolation, low-frequency interpolation” is viable, not just the scheme introducing $\lambda$ described above. Readers can try this themselves.

Personal Test

#

As a scheme claimed to increase LLM Context length without fine-tuning, I was shocked when I first saw NTK-aware Scaled RoPE and couldn’t wait to test it. After all, based on the experience from 《The Road to Transformer Upgrades: 9. A New Idea for Global Length Extrapolation》, many mainstream schemes failed on the “GAU+Post Norm” combination I prefer. How would this method fare?

When $k$ is set to 8, the comparison results are as follows (regarding the difference between “repeat” and “non-repeat”, you can refer here):

The results reported above are all without long text fine-tuning. Baseline is extrapolation, PI (Positional Interpolation) is interpolation based on Baseline, and NTK-RoPE is NTK-aware Scaled RoPE based on Baseline. The option with $\log n$ means that the scaling from 《Viewing Attention’s Scale Operation from Entropy Invariance》 was added during pre-training. This variant is considered because I feel that although NTK-RoPE solves the length generalization problem for RoPE, it does not solve the lack of attention concentration problem.

The experimental results in the table fully meet expectations:

1. Direct extrapolation does not work well.

2. Interpolation also works poorly if not fine-tuned.

3. NTK-RoPE achieves non-trivial (but somewhat degraded) extrapolation results without fine-tuning.

4. Adding $\log n$ to concentrate attention is indeed helpful.

Therefore, NTK-RoPE successfully becomes the second scheme I have tested that effectively extends LLM Context length without fine-tuning (the first, naturally, being NBCE). I applaud the proposer’s excellent insight once again! What’s even more encouraging is that NTK-RoPE performs significantly better on “repeat” extrapolation than on “non-repeat” extrapolation, indicating that this modification preserves global dependencies rather than simply localizing attention.

Summary (formatted)

#

This article interprets RoPE from the perspective of $\beta$-based encoding and uses this to introduce some current progress in the open-source community regarding Long Context, including a modified scheme that can increase Context length without fine-tuning.

@online{kexuefm-9675,
        title={The Road to Transformer Upgrades: 10. RoPE is a $\beta$-Based Encoding},
        author={苏剑林},
        year={2023},
        month={07},
        url={\url{https://kexue.fm/archives/9675}},
}